Цифровая библиотека

Интернет-библиотека по школьным предметам от «Онлайн-школы». Библиотека поможет решить домашнее задание, подготовиться к контрольной и вспомнить прошлые темы.

Например: формулы сокращенного умножения

Выбери класс

Выбери все классы

Все предметы
7 класс
Геометрия
Свойства равнобедренного треугольника

Геометрия 7 класс Геометрия 7 класс

Конспект урока: Свойства равнобедренного треугольника

Треугольники

08.10.2024

1959

Свойства равнобедренного треугольника

План урока

Равнобедренный треугольник;
Свойства равнобедренного треугольника.

Цели урока

Знать определение равнобедренного треугольника и названия его элементов;
Знать определение равностороннего треугольника;
Знать свойства равнобедренного треугольника;
Уметь применять определение и свойства равнобедренного треугольника при решении задач.

Разминка

Вспомните определение треугольника, назовите его элементы.
Что такое медиана треугольника?
Что такое биссектриса треугольника?
Что такое высота треугольника?

Равнобедренный треугольник

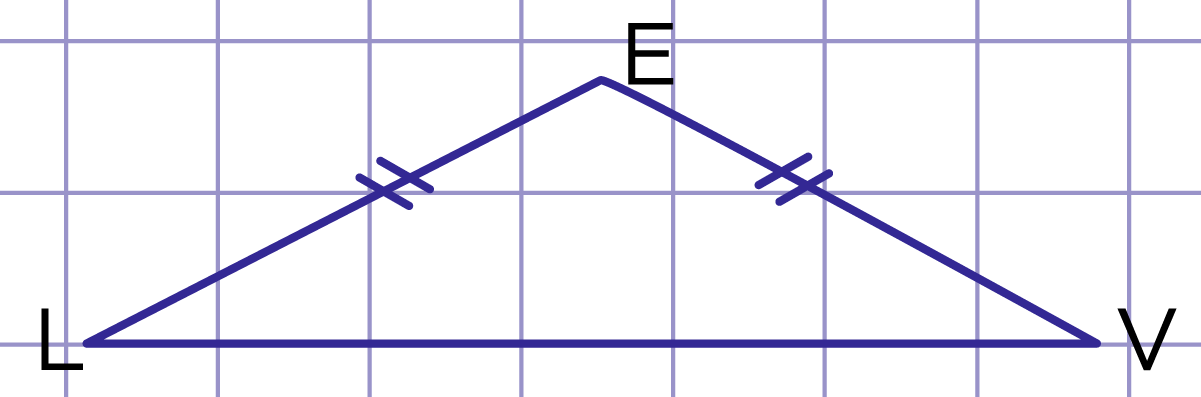Рис. 1. Треугольник LEV - равнобедренный

Равнобедренный треугольник - это треугольник, у которого две стороны равны.

Равные стороны называются боковыми сторонами.

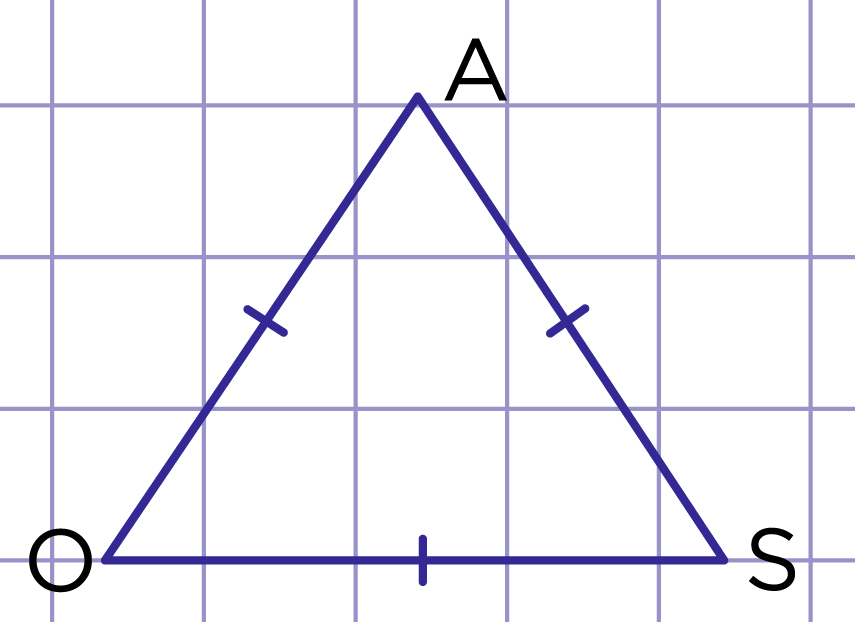Рис. 2. Треугольник OSA - равносторонний

Третья сторона - основанием равнобедренного треугольника.

Равносторонний треугольник - это треугольник, у которого все стороны равны.

Пример 1

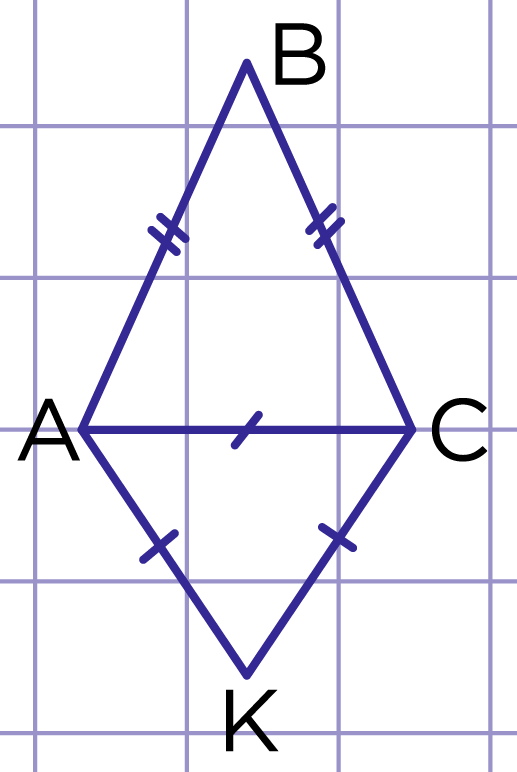Рис. 3. Пример 1

Периметр треугольника $A K C$ равен 30 см, периметр треугольника $A B C$ в 1,5 раза больше (рис. 3). Найти длину $A B$ .

Решение

$∆ A K C$ - равносторонний, $A K = K C = A C = 30 : 3 = 10$ (см).
30 см · 1,5 = 45 см - периметр треугольника $A B C$ .
$∆ A B C$ - равнобедренный, $A B = B C$ , $A C = 10$ см. $A B = (45 - 10) : 2 = 17, 5$ см.

Ответ: $17, 5$ см.

Упражнение 1

Начертите равнобедренный треугольник так, чтобы все углы были острые.
Начертите равнобедренный треугольник так, чтобы один из его углов был прямым.
Начертите равнобедренный треугольник так, чтобы один из его углов был тупым.

Свойства равнобедренного треугольника

Теорема

В равнобедренном треугольнике углы при основании равны.

Доказательство

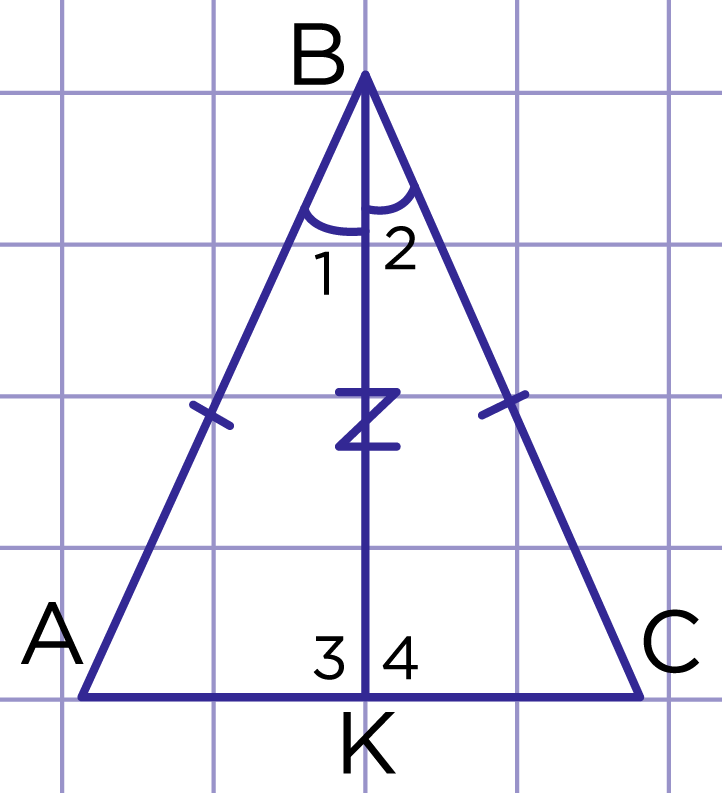Рис. 4.

Рассмотрим треугольник $A B C$ – равнобедренный, $A B = B C$ (рис. 4). Надо доказать, что $∠ A = ∠ C$ . Проведём в треугольнике $A B C$ биссектрису $B K$ .

1) Рассмотрим $∆ A B K$ и $∆ C B K$ :

$A B = B C$ - по условию,

$∠ 1 = ∠ 2$ , т. к. $B K$ - биссектриса,

$B K$ - общая сторона.

Тогда $∆ A B K = ∆ C B K$ по двум сторонам и углу между ними.

2) Треугольники равны, значит, соответствующие элементы равны, т.е. $∠ A = ∠ C$ .

Теорема доказана.

Теорема

В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.

Доказательство

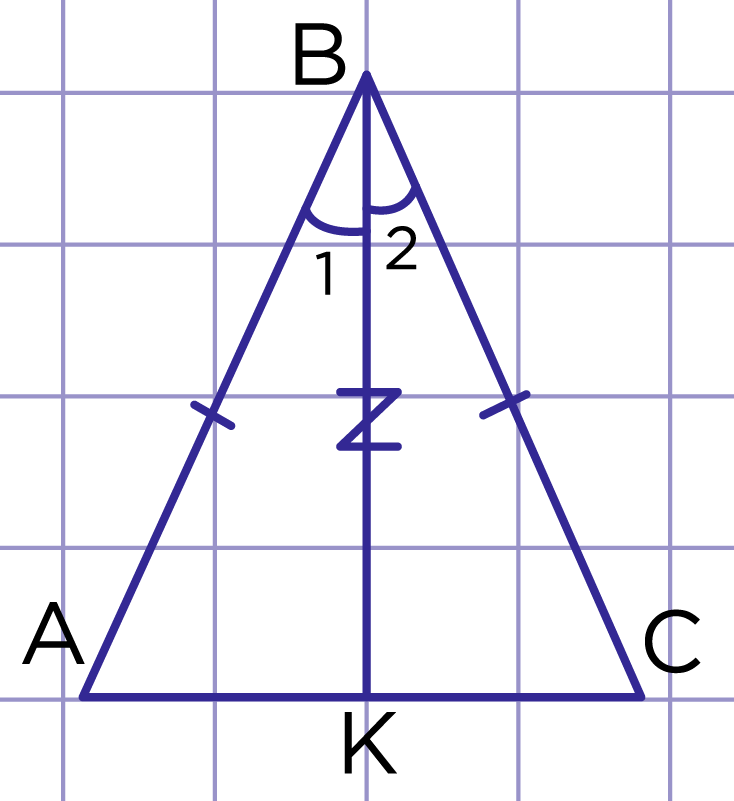Рис. 5.

Рассмотрим треугольник $A B C$ – равнобедренный, $A B = B C$ , $B K$ - биссектриса (рис. 5). Надо доказать, что $B K$ является медианой и высотой.

1) Рассмотрим $∆ A B K$ и $∆ C B K$ :

$A B = B C$ - по условию,

$∠ 1 = ∠ 2$ , т. к. $B K$ - биссектриса,

$B K$ - общая сторона.

Тогда $∆ A B C = ∆ C B K$ по двум сторонам и углу между ними.

2) $A K = C K$ – соответственные элементы в равных треугольниках, т. е. точка $K$ – середина $A C$ , значит, $B K$ – медиана равнобедренного треугольника.

3) $∠ A K B = ∠ C K B$ - соответственные элементы в равных треугольниках. $∠ A K B + ∠ C K B = 180 °$ , т. к. это смежные углы, тогда $∠ A K B = ∠ C K B = 90 °$ , значит, $B K ⊥ A C$ , т.е. $B K$ – высота равнобедренного треугольника.

Теорема доказана.

Так как биссектриса, высота и медиана, проведённые к основанию, совпадают, то будут верными утверждения:

В равнобедренном треугольнике высота, проведённая к основанию, является медианой и биссектрисой.
В равнобедренном треугольнике медиана, проведённая к основанию, является высотой и биссектрисой.

Пример 2

Треугольник $T O M$ - равнобедренный, $T O = O M$ . На высоте $O H$ взята точка $K$ . Докажите, что треугольник $T K M$ - равнобедренный.

Решение

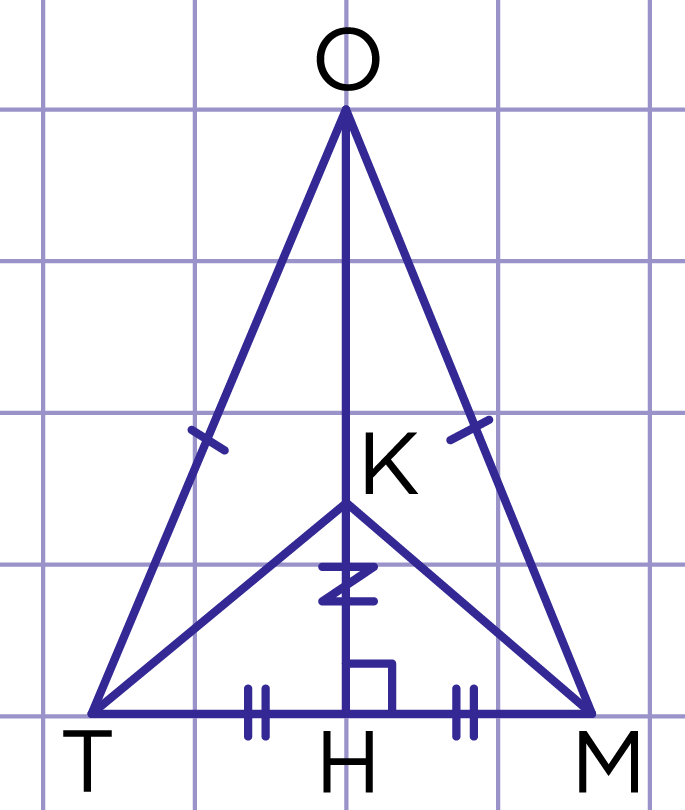Рис. 6. Пример 2

1) Рассмотрим треугольник $T O M$ (рис. 6). Высота $O H$ проведена к основанию, значит, $O H$ – медиана, т. е. $T H = H M$ .

2) Рассмотрим $∆ T K H$ и $∆ M K H$ :

$T H = H M$ ,

$K H$ - общая,

$∠ T H K = ∠ M H K = 90 °$ т. к. $O H$ - высота.

Тогда $∆ T K H$ и $∆ M K H$ равны по двум сторонам и углу между ними.

3) $T K = K M$ как соответственные стороны в равных треугольниках, значит, $∆ T K M$ – равнобедренный.

Что и требовалось доказать.

Упражнение 2

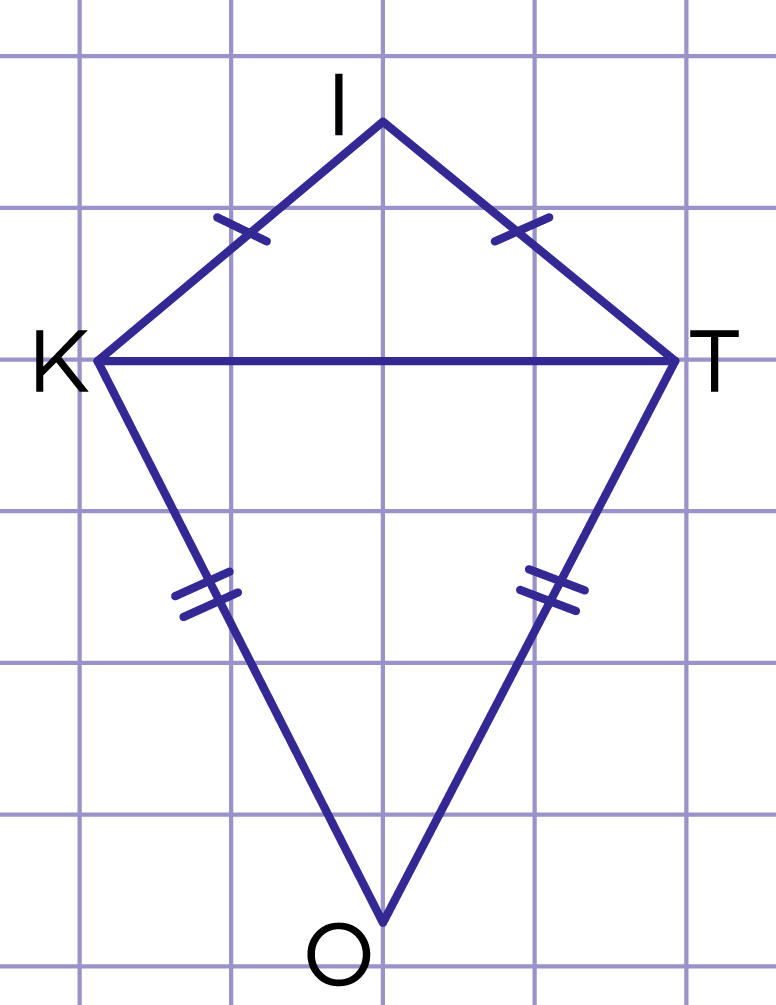Рис. 7. Упражнение 2

1) Треугольники $K O T$ и $K I T$ - равнобедренные, основание $K T$ - общее (рис. 7). Докажите, что $∠ O K I = ∠ O T I$ .

2) $K H$ - высота равнобедренного треугольника $B U K$ с основанием $B U$ .

Точка $D$ лежит на $K H$ . Докажите, что $∆ D U B$ - равнобедренный.

3) Докажите, что в равностороннем треугольнике все углы равны.

Контрольные вопросы

Какой треугольник называется равнобедренным?
Как называются стороны равнобедренного треугольника?
Какой треугольник называется равносторонним?
Назовите свойство равнобедренного треугольника об углах при его основании.
Назовите свойство равнобедренного треугольника о биссектрисе, проведенной к основанию.

Ответы

Упражнение 1

Прямой угол должен лежать против основания.
Тупой угол должен лежать против основания.

Упражнение 2

Указание: представьте каждый из углов $O K I$ и $O T I$ в виде суммы углов.
Указание: докажите равенство треугольников $K B H$ и $K U H$ , $D B H$ и $D U H$ .

Предыдущий урок

Третий признак равенства треугольников

Треугольники

Следующий урок

Прямоугольные треугольники

Треугольники

Урок подготовил(а)

Валерия Александровна

Учитель математики

Опыт работы: более 20 лет

Строение и жизнедеятельность рыб

Биология
Умножение одночлена на многочлен

Алгебра
Правописание союзов

Русский язык

Зарегистрируйся, чтобы присоединиться к обсуждению урока

Добавьте свой отзыв об уроке, войдя на платфому или зарегистрировавшись.

Отзывы об уроке:

Пока никто не оставил отзыв об этом уроке