Цифровая библиотека

Интернет-библиотека по школьным предметам от «Онлайн-школы». Библиотека поможет решить домашнее задание, подготовиться к контрольной и вспомнить прошлые темы.

Например: формулы сокращенного умножения

Выбери класс

Выбери все классы

Все предметы
8 класс
Алгебра
Решение неравенств с одной переменной

Алгебра 8 класс Алгебра 8 класс

Конспект урока: Решение неравенств с одной переменной

Решение уравнений и неравенств

20.04.2024

2050

Решение неравенств с одной переменной

План урока

Решение неравенств с одной переменной
Примеры решения неравенств с одной переменной

Цели урока

Знать определение решения неравенства с одной переменной
Знать правила переходов от одного неравенства к другому, ему равносильному
Знать определение линейного неравенства с одной переменной
Уметь решать линейные неравенства с одной переменной

Разминка

Прочитайте неравенство и назовите соответствующий ему числовой промежуток: а) $x < - 3$ ; б) $x \geq 7$ ; в) $- 2 < x < 3$ ; г) $- 1 \leq x \leq 1$

Решение неравенств с одной переменной

Неравенство $2 x + 3 > 4$ обращается в верное числовое равенство только при некоторых значениях переменной. Например, при $x = 1$ . Если же вместо $x$ подставить 0, то неравенство верным не будет. В таком случае говорят, что 1 является решением неравенства $2 x + 3 > 4$ или удовлетворяет этому неравенству. Заметим, что, например, числа 2, 10, 15 также являются решениями этого неравенства, а числа -3, 0,2 не являются.

Решением неравенства с одной переменной называется значение переменной, которое обращает его в верное числовое неравенство.

Решить неравенство — значит найти все его решения или доказать, что решений нет.

Неравенства, имеющие одни и те же решения, называются равносильными . Неравенства, не имеющие решений, также считают равносильными.

При решении неравенств используются следующие свойства:

1) Если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится равносильное ему неравенство.

2) Если обе части неравенства умножить или разделить на одно и то же положительное число, то получится равносильное ему неравенство;
если обе части неравенства умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится равносильное ему неравенство.

Примеры решения неравенств с одной переменной

Рассмотрим примеры решения неравенств.

Пример 1

Решить неравенство $6 + x < 3 - 2 x$ .

Решение

Перенесём слагаемое $- 2 x$ из правой части неравенства с противоположным знаком в левую часть, а число 6 из левой части в правую с противоположным знаком:

$x + 2 x < 3 - 6$ .

Приведем подобные слагаемые:

$3 x < - 3$ .

Разделим обе части неравенства на положительное число 3:

$x < - 1$

Этому неравенству отвечает открытый числовой луч $(- \infty; - 1)$ (рис. 1).

Ответ: $(- \infty; - 1)$ .

Пример 2

Решить неравенство $3 (2 + x) < 4 - x$ .

Решение

Раскроем скобки в левой части неравенства:

$6 + 3 x < 4 - x$ .

Перенесём слагаемое $- x$ из правой части неравенства с противоположным знаком в левую часть, а число 6 из левой части в правую с противоположным знаком:

$3 x + x < 4 - 6$ .

Приведем подобные слагаемые:

$4 x < - 2$ .

Разделим обе части неравенства на положительное число 4:

$x < - 0, 5$

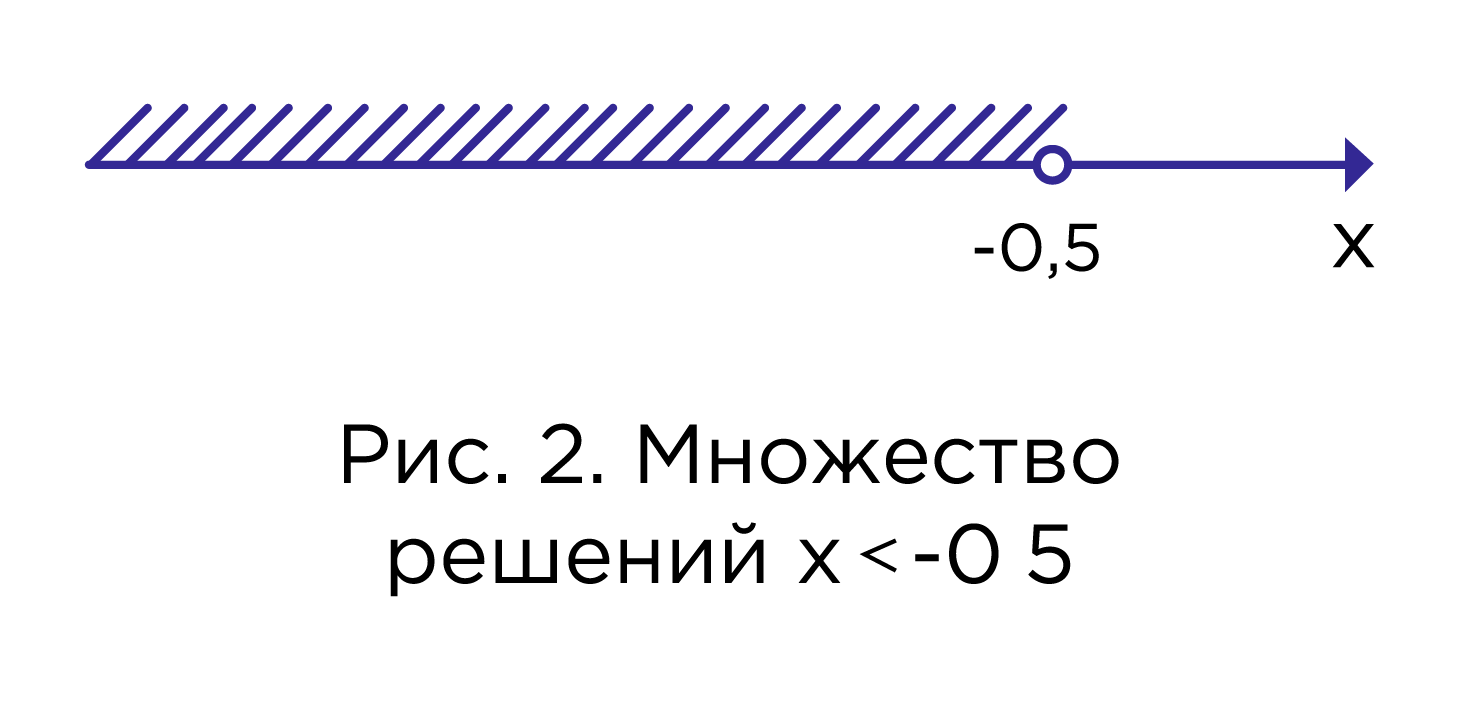
Этому неравенству отвечает открытый числовой луч $(- \infty; - 0, 5)$ (рис. 2).

Ответ: $(- \infty; - 0, 5)$ .

Пример 3

Решить неравенство $\frac{x - 1}{3} - 2 x < \frac{3 x + 1}{2}$ .

Решение

Умножим обе части неравенства на наименьший общий знаменатель дробей, входящих в неравенство:

$\frac{6 (x - 1)}{3} - 12 x < \frac{6 (3 x + 1)}{2},$

$2 x - 2 - 12 x < 9 x + 3,$

$2 x - 12 x - 9 x < 3 + 2$

Отсюда,

$- 19 x < 5,$

$x > - \frac{5}{19}$ .

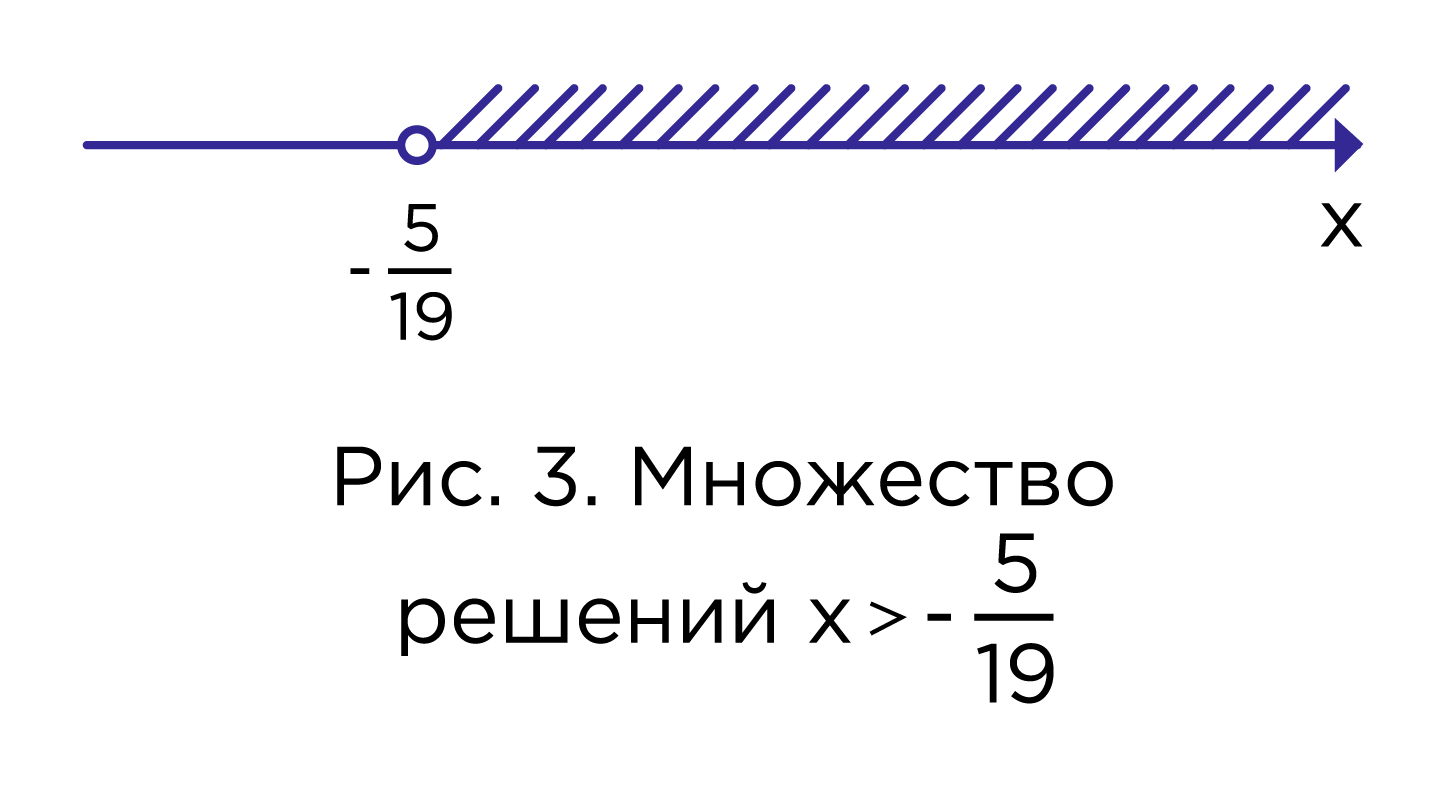
Получаем открытый луч $(- \frac{5}{19}; + \infty)$ .

Ответ: $(- \frac{5}{19}; + \infty)$ .

Неравенства вида $a x > b$ или $a x < b$ , где a и b — некоторые числа, называют линейными неравенствами с одной переменной .

В некоторых случаях может случиться, мы придем к неравенству вида $0 \cdot x < b$ и $0 \cdot x > b$ . Такие неравенства либо не имеют решения, либо их решением является любое число.

Например, неравенство $0 \cdot x < 12$ , равносильное $0 < 12$ , выполняется всегда, поэтому решением будет вся числовая прямая $(- \infty; + \infty)$ . Неравенство $0 \cdot x < - 3$ , равносильно $0 < - 3$ , не является верным, поэтому не имеет решения.

Упражнение 1

Решите неравенство:

а) $4 + 12 x > 7 + 13 x$ ;

б) $3 (1 - x) + 2 (2 - 2 x) < 0$ ;

в) $- (4 - x) \leq 2 (3 + x)$ ;

г) $\frac{2 x}{5} - x > 3$ ; д) $x + \frac{x}{4} \geq 2$ ; e) $\frac{2 x}{3} - \frac{x - 1}{6} + \frac{x + 2}{2} \geq 0 .$

Контрольные вопросы

1. Что называется решением неравенства?

2. Всегда ли неравенство имеет решение?

3. Какие свойства используют при решении неравенств?

4. Какие неравенства называются линейными?

Ответы

Упражнение 1

а) $(- \infty; - 3)$ ; б) $(1; + \infty)$ ; в) $[- 10; + \infty)$ ; г) $(- \infty; - 5)$ ; д) $[1, 6; + \infty)$ ;

е) $[- 1 \frac{1}{6}; + \infty) .$

Предыдущий урок

Решение задач с помощью рациональных уравнений

Решение уравнений и неравенств

Следующий урок

Решение неравенств с одной переменной

Решение уравнений и неравенств

Урок подготовил(а)

Валерия Александровна

Учитель математики

Опыт работы: более 20 лет

Вынесение множителя за знак корня и внесение его под знак корня

Алгебра
Человек и вода

География
Наука в современном обществе

Обществознание

Зарегистрируйся, чтобы присоединиться к обсуждению урока

Добавьте свой отзыв об уроке, войдя на платфому или зарегистрировавшись.

Отзывы об уроке:

Пока никто не оставил отзыв об этом уроке