Конспект урока: Уравнение x^2=a. Нахождение приближенных значений квадратного корня

1) Если a < 0, то уравнение корней не имеет, поскольку не существует числа, квадрат которого был бы равен отрицательному числу. 

2) Если a = 0, то уравнение имеет единственный корень, равный нулю, т.к. существует единственное число 0, квадрат которого равен нулю. 

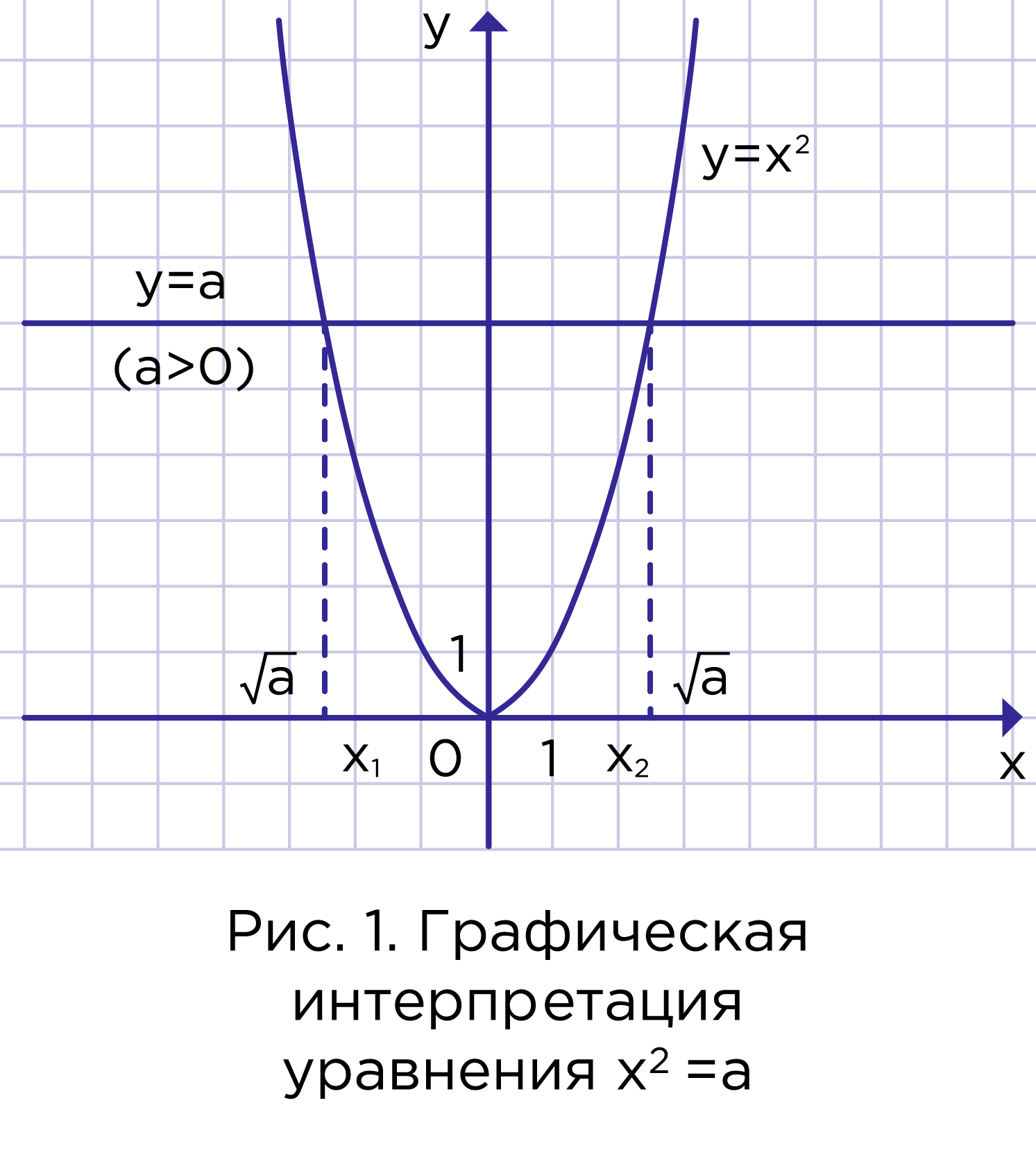
3) Если a > 0, то уравнение имеет два корня. Рассмотрим графическую модель этого уравнения (рис. 1). Прямая y = a при a > 0 пересекает параболу $y=x^2$ в двух точках. Обозначим абсциссы точек пересечения $x_1$ и $x_2$. Тогда ${x_1}^2=a$, и ${x_2}^2=a$, значит, числа $x_1$ и $x_2$ – корни уравнения $x^2=a$. Т.к. $x_2$ есть положительное число, квадрат которого равен a, то $x_2$ является арифметическим квадратным корнем из a, т.е. $x_2=\sqrt{a}$ . Так как $x_1$ есть число, противоположное $x_2,$ то $x_1=-\sqrt{a}$ . 

Таким образом, можно сделать вывод:

Решение

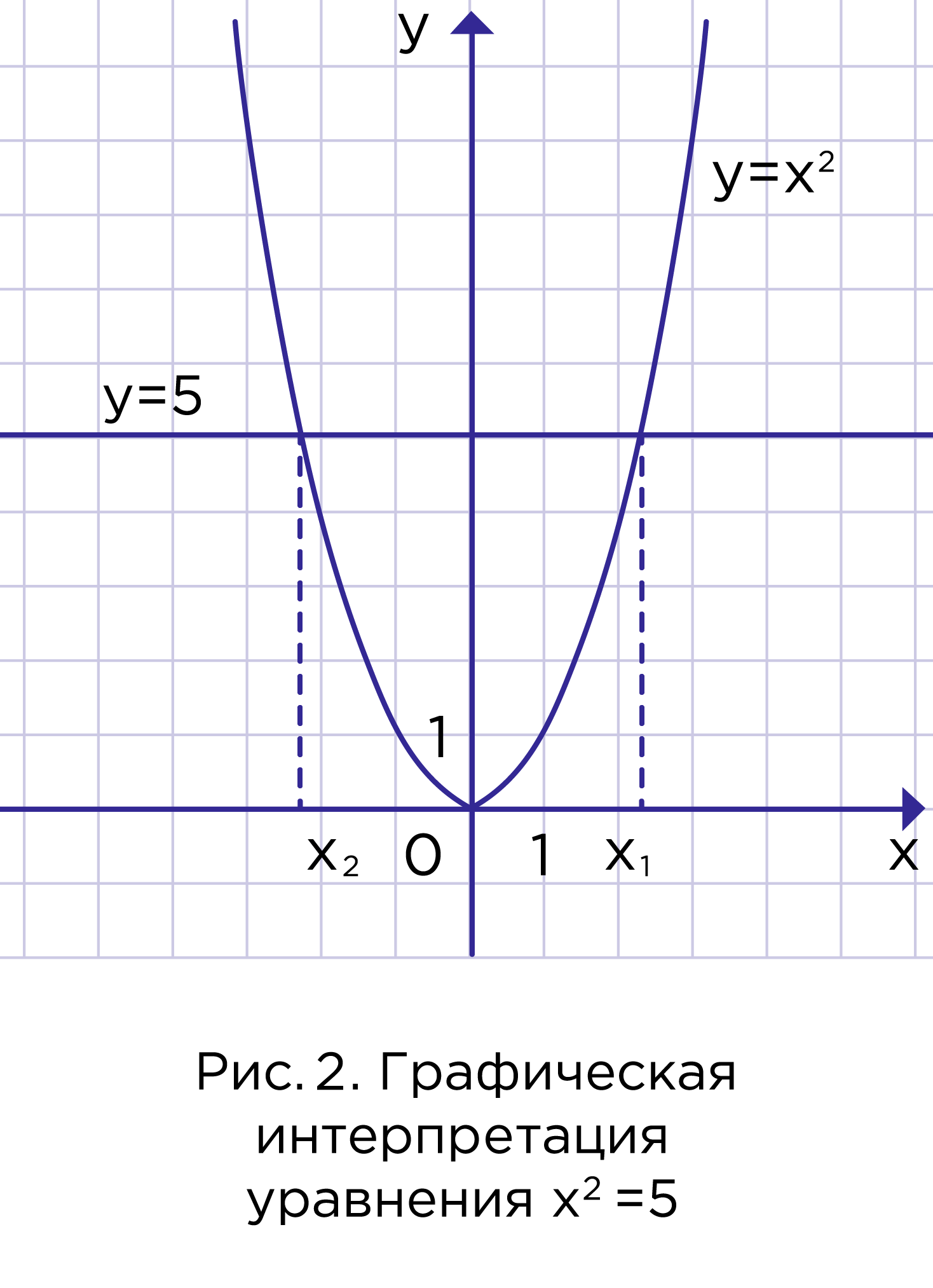
Графическая иллюстрация уравнения $x^2=5$ на рисунке 2. Это уравнение имеет два корня $x_1=\sqrt{5 }и x_2=-\sqrt{5}$, но эти числа уже иррациональные, т.к. не существует рационального числа, квадрат которого равен 5. С помощью графика можно определить приближенное значение этих корней: $x_1\approx 2,2, x_2\approx -2,2$. 

Ответ: $-\sqrt{5}, \sqrt{5}.$