Конспект урока: Применение производной к построению графиков функций

План урока

• Схема исследования и построения графиков функций;
• Особенности исследования и построения графиков чётных и нечётных функций.

Цели урока

• Знать общую схему исследования функции с помощью производной;
• Уметь применять производную при исследовании функции.

Разминка

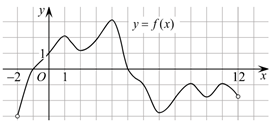Рис. 1.

1. Какой знак имеет производная функции на промежутке возрастания (убывания)?
2. Чему равна производная дифференцируемой функции в точке экстремума?
3. На рисунке 1 изображен график функции $y = f\left(x\right)$, определенной на интервале (−2; 12). Найдите сумму точек экстремума функции $f\left(x\right)$.

Схема исследования и построения графиков функций

С помощью понятия производной мы можем определить промежутки возрастания и убывания функции, найти критические точки, а также точки максимума и минимума функции. Всё это даёт возможность применять производную при построении графиков функций. Перед построением графика функции проводится её исследование и часть сведений об исследуемой функции получают с помощью производной. Однако, помимо этих данных, для более точного построения графиков функции нам необходимы еще некоторые сведения. Приведем схему исследования функций, которой и будем пользоваться в дальнейшем.

Результаты исследования удобно записывать в виде таблицы.

Кроме того, желательно найти точки пересечения с осями координат. Для более точного построения графика функции можно найти ещё несколько точек.

Построить график функции $y=2x^3-x^2-4x$.

Решение

1. Найдём область определения функции: $D\left(y\right)=\left(-\infty ;+\infty \right)$.

2. Найдём производную функции: $y^{\text{'}}={\left(2x^3-x^2-4x\right)}^{\text{'}}=6x^2-2x-4$.

3. Найдём критические точки: $6x^2-2x-4=0$.

$D={\left(-2\right)}^2-4·6·\left(-4\right)=4+96=100$

$x_1=\frac{2-\sqrt{100}}{12}=-\frac{8}{12}=-\frac{2}{3}$

$x_2=\frac{2+\sqrt{100}}{12}=1$

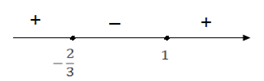Рис. 2.

4. Найдём промежутки возрастания и убывания (рис. 2):

 

функция возрастает на интервалах $\left(-\infty ; -\frac{2}{3}\right)$ и $\left(1; +\infty \right)$.                                           

функция убывает на интервале $\left(-\frac{2}{3};1\right)$.

5. Найдём точки экстремума и значения функции в этих точках (рис. 2): 

$x=-\frac{2}{3}$ - точка максимума,

$f\left(-\frac{2}{3}\right)=2·{\left(-\frac{2}{3}\right)}^3-{\left(-\frac{2}{3}\right)}^2-4·\left(-\frac{2}{3}\right)=\frac{44}{27}$.

$x=1$ - точка минимума,

$f\left(1\right)=2-1-4=-3$

Представим результаты исследования в виде таблицы:

Найдём точки пересечения с осями координат:

(0;0) - точка пересечения с осью $Oy$;

$2x^3-x^2-4x=0$

$x·\left(2x^2-x-4\right)=0$

$x_1=0; x_2=\frac{\left(1-\sqrt{33}\right)}{4}; x_3=\frac{1+\sqrt{33}}{4}$ - абсциссы точек пересечения с осью $Ox$.

Таким образом, график функции пересекает координатные оси в точках $\left(0;0\right); \left(\frac{1-\sqrt{33}}{4};0\right)$ и $\left(\frac{1+\sqrt{33}}{4};0\right)$.

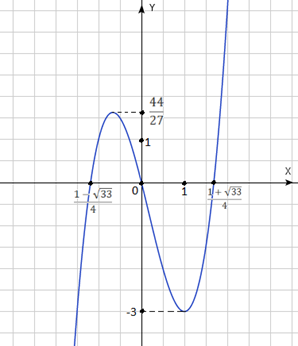Рис. 3.

Построим график функции (рис. 3).                                                                                                          

Особенности исследования и построения графиков чётных и нечётных функций

Для построения графика чётной (нечётной) функции достаточно исследовать свойства и построить её график для $x>0$, а затем отразить его симметрично относительно оси ординат (начала координат).

Построить график функции $y=-x^4+5x^2-4$.

Решение

1. Найдём область определения функции: $D\left(y\right)=\left(-\infty ;+\infty \right)$

2. Исследуем функцию на чётность, нечётность

$f\left(-x\right)=-{\left(-x\right)}^4+5·{\left(-x\right)}^2-4=-x^4+5x^2-4=f\left(x\right)\Rightarrow$ данная функция является чётной. Таким образом, исследовать функцию и строить график будем сначала при $x\ge 0$.

3. Найдём производную функции: $y^{\text{'}}={\left(-x^4+5x^2-4\right)}^{\text{'}}=-4x^3+10x$.

4. Найдём стационарные точки на промежутке $[0; +\infty )$: 

$-4x^3+10x=0$

$2x·\left(-2x^2+5\right)=0$

$x_1=0,x_2=\sqrt{2,5}$

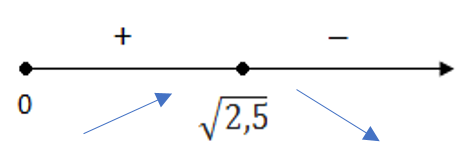Рис. 4.

5. Найдём промежутки возрастания и убывания (рис. 4):

 

Функция возрастает на интервале $\left(0; \sqrt{2,5}\right)$.

Функция убывает на интервале $\left(\sqrt{2,5};+\infty \right)$.                                                                               

6. Найдём точки экстремума и значения функции в них:

$f\left(0\right)=-4$;

$x=\sqrt{2,5}$ точка максимума, $f\left(\sqrt{2,5}\right)=-{\left(\sqrt{2,5}\right)}^4+5{\left(\sqrt{2,5}\right)}^2-4=2,25$.

Представим результаты исследования в виде таблицы:

Найдём точки пересечения с осями координат на промежутке $[0; +\infty )$:

Если $x=0$, то $y=-4\Rightarrow (0; -4)$– точка пересечения с осью $Oy$.

Если $y=0$, то $-x^4+5x^2-4=0$

$x_1=1; x_2=2\Rightarrow (1; 0) и (2; 0)$ – точки пересечения с осью $Ox$.

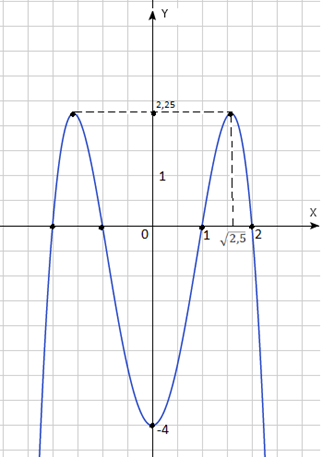Рис. 5.

Используя результаты исследования, строим график функции при $x\ge 0$. График этой функции при $x<0$ строим с помощью симметрии относительно оси $Oy$ (рис. 5).

1. Постройте графики функций:

 а) $y=x^3-3x^2+4$;  б) $y=3x^5-5x^3$; в) $y=\frac{x^2-1}{x^2+1}$.

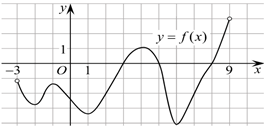Рис. 6.

2. На рисунке 6 изображен график функции $y = f\left(x\right)$, определенной на интервале $(-3; 9)$. Найдите:

а) промежутки, в которых производная функции меньше нуля; 

б) промежутки, в которых производная функции больше нуля;

в) точки в которых производная равна нулю.