Геометрический смысл производной

План урока

Геометрический смысл производной;
Уравнение касательной к графику функции.

Цели урока

Знать, что называют угловым коэффициентом прямой, углом между прямой и осью $O x$ ;
Знать в чем состоит геометрический смысл производной;
Знать уравнение касательной к графику функции;
Уметь решать задачи на геометрический смысл производной;
Уметь записывать уравнение касательной к графику функции.

Разминка

Построить графики функций:
а) $y = 3 - \frac{1}{2} x$ ; б) $y = 2 x - 1$ .
Найти тангенс угла наклона построенной прямой к оси $O x$ . Возрастающей или убывающей являются эти функции?
Вычислить производную функций:
а) $y = \sin 3 x - \cos 2 x$ ;
б) $y = ctg x - tg (x + \frac{π}{3})$ ;
в) $y = ctg x \cdot \cos (3 x + 4)$
При каких условиях графики функций $y = k_{1} x + b_{1}$ и $y = k_{2} x + b_{2}$ параллельны, совпадают, пересекаются?

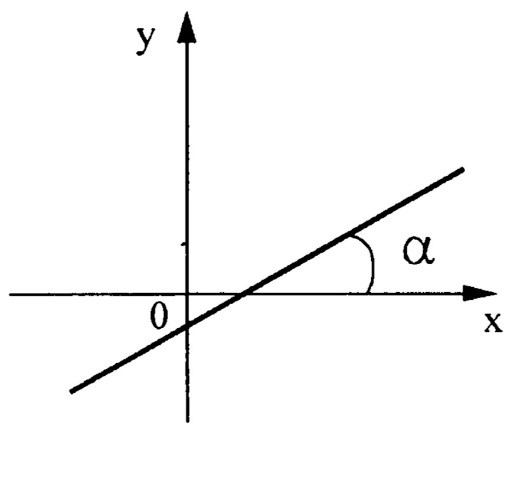Рис. 1. График функции y=kx+b
при k>0

Пусть дана линейная функция $f (x) = k x + b$ , графиком которой является прямая. Число $k$ называют угловым коэффициентом прямой. $k = tg α$ , где $α$ — угол между этой прямой и положительным направлением оси $O x$ .

Если $k > 0$ , то функция возрастает, $α \in (0; \frac{π}{2})$ (рис. 1).

Если $k < 0$ , то функция убывает, $α \in (\frac{π}{2}; π)$ (рис. 2).

В чем же геометрический смысл производной функции?

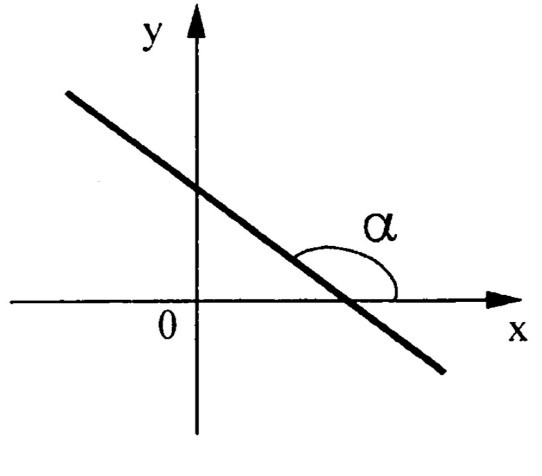Рис. 2. График функции y=kx+b
при k<0

Рассмотрим график функции $y = f (x)$ . Проведем секущую через любые две точки, например, секущую $A B$ (рис. 3). Пусть $A (x; f (x))$ , $B (x + h; f (x + h))$ , $C (x + h; f (x))$ , $k (h)$ — угловой коэффициент прямой $A B$ . $k (h) = tg α$ . Так как прямая $A C$ параллельна оси $O x$ , то $∠ B A C = α$ . Из прямоугольного треугольника $A B C$ имеем

$k (h) = tg ∠ B A C = \frac{B C}{A C} = \frac{f (x + h) - f (x)}{x + h - x} = \frac{f (x + h) - f (x)}{h}$ .

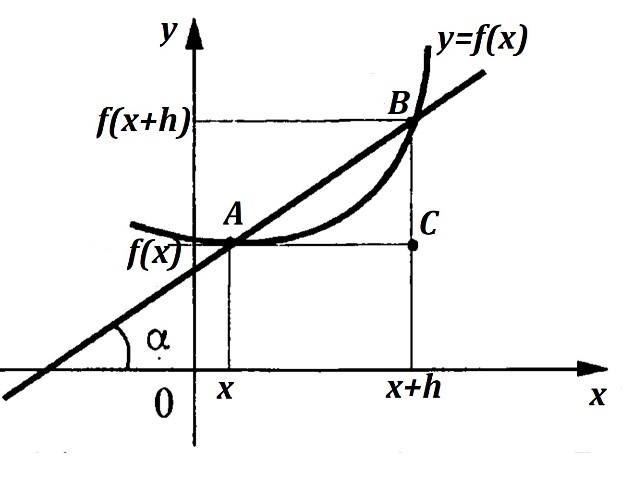Рис. 3. Геометрический смысл производной

Зафиксируем $x$ , тогда точка $A$ будет неподвижна. Если $h \to 0$ , то точка $B$ , двигаясь по графику функции, стремится к точке $A$ . Предел $k (h)$ при $h \to 0$ существует и равен производной функции $f (x)$ . Прямая $A B$ стремится занять положение некоторой прямой, которую называют касательной к графику функции $y = f (x)$ . Получили, что

$f^{'} (x) = tg α$ .

Геометрический смысл производной состоит в том, что значение производной функции $f (x)$ в точке $x$ равно угловому коэффициенту касательной к графику функции в точке $(x; f (x))$ .

Пример 1

Найти угол между касательной к графику функции $y = \frac{1}{3} x^{3}$ в точке с абсциссой $x_{0} = 1$ и осью $O x$ .

Решение

Найдем угловой коэффициент касательной к функции $y = \frac{1}{3} x^{3}$ в точке с абсциссой $x_{0}$ , т. е. значение производной этой функции при $x = 1$ .

$f^{'} (x) = {(\frac{1}{3} x^{3})}^{'} = x^{2}$ .

$tg α = f^{'} (1) = 1$ , тогда $α = arctg 1 = \frac{π}{4}$ .

Ответ: $\frac{π}{4}$ .

Упражнение 1

Найти угол между касательной к графику функции $y = f (x)$ в точке с абсциссой $x_{0}$ и осью $O x$ :

1. $f (x) = 2 x^{2}, x_{0} = 1$ ;

2. $f (x) = \sin 4 x, x_{0} = \frac{π}{16}$ .

Уравнение касательной к графику функции

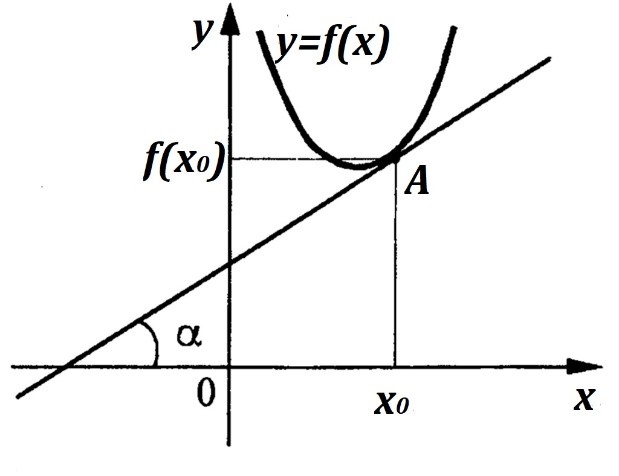Рис. 4. График функции y=f(x) и касательная к нему

Рассмотрим график функции $y = f (x)$ и касательную к нему (рис. 4). Выведем уравнение касательной к графику дифференцируемой функции в точке $A (x_{0}; f (x_{0}))$ .

Касательной к графику является прямая, общий вид которой $y = k x + b$ . Так как $k = tg α = f^{'} (x_{0})$ , то уравнение касательной можно переписать как $y = f^{'} (x_{0}) x + b$ . Точка $A (x_{0}; f (x_{0}))$ принадлежит касательной, тогда ее координаты удовлетворяют уравнению касательной, т. е. $f (x_{0}) = f^{'} (x_{0}) x_{0} + b$ , откуда $b = f (x_{0}) - f^{'} (x_{0}) x_{0}$ '.

Итак, уравнение касательной $y = f^{'} (x_{0}) x + f (x_{0}) - f^{'} (x_{0}) x_{0}$ или $y = f (x_{0}) + f^{'} (x_{0}) (x - x_{0})$ .

Уравнение касательной к графику функции в точке с абсциссой $x_{0}$

$y = f (x_{0}) + f^{'} (x_{0}) (x - x_{0})$ (1)

Алгоритм составления уравнения касательной к графику функции $y = f (x)$ в точке с абсциссой $x_{0}$ .

1. Найти производную функции $f^{'} (x)$ .

2. Вычислить $f^{'} (x_{0})$ .

3. Вычислить $f (x_{0})$ .

4. Подставить найденные числовые значения в формулу (1) и упростить выражение.

Пример 2

Записать уравнение касательной к графику функции $f (x) = 2 x^{3} - 3 x$ в точке с абсциссой $x_{0} = 2$ .

Решение

Для записи уравнения касательной к графику функции идем по алгоритму:

1. $f^{'} (x) = 6 x^{2} - 3$ .

2. $f^{'} (x_{0}) = f^{'} (2) = 21$ .

3. $f (x_{0}) = f (2) = 10$ .

4. $y = 10 + 21 (x - 2) = 21 x - 32$ .

Ответ: $21 x - 32$ .

Пример 3

Найти точки графика функции $f (x) = \frac{1}{3} x^{3} - \frac{1}{2} x^{2} + 3 \frac{1}{3}$ , в которых касательная к нему параллельна прямой $y = 2 x$ .

Решение

Угловой коэффициент прямой $y = 2 x$ равен $2$ . Для того, чтобы касательная к графику функции $f (x)$ была параллельна $y = 2 x$ нужно, чтобы их угловые коэффициенты были равны, т. е. должно выполняться равенство $f^{'} (x) = 2$ . Тогда $x^{2} - x = 2$ , откуда $x_{1} = - 1, x_{2} = 2$ . Если $x_{1} = - 1$ , то $y_{1} = f (- 1) = 2, 5$ .

Если $x_{2} = 2$ , то $y_{2} = f (2) = 4$ .

Так как выполнение равенства $f^{'} (x) = 2$ предполагает не только параллельность прямых, но и их совпадение, проверим принадлежность точек $(- 1; 2, 5)$ и $(2; 4)$ прямой $y = 2 x$ . Очевидно, что $(- 1; 2, 5)$ не принадлежит прямой, поэтому касательная в этой точке к графику функции $f (x)$ параллельна прямой $y = 2 x$ , а точка $(2; 4)$ принадлежит ей, поэтому касательная в этой точке и есть прямая $y = 2 x$ , т. е. точка $(2; 4)$ не удовлетворяет условию задачи.

Ответ: $(- 1; 2, 5)$ .

Пример 4

Найдите расстояние от начала координат до касательной, проведенной к графику функции $f (x) = \sqrt{x}$ в точке $(1; 1)$ .

Решение

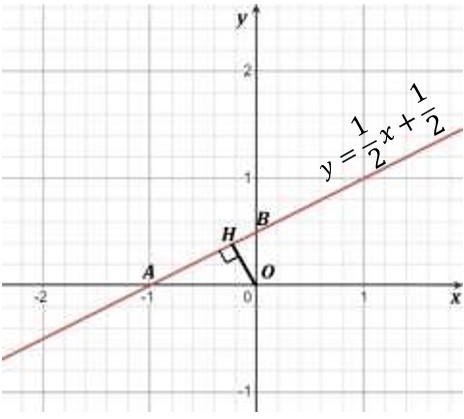Рис. 5

Напишем уравнение касательной к графику функции $f (x) = \sqrt{x}$ в точке с абсциссой, равной $1$ . Для этого найдем производную функции $f (x)$ , ее значение в точке $x = 1$ и значение самой $f (x)$ в точке $x = 1$ : $f^{'} (x) = \frac{1}{2 \sqrt{x}}$ , $f (1) = 1$ , $f^{'} (1) = \frac{1}{2}$ .

Тогда уравнение касательной к графику функции $f (x)$ имеет вид:

$y = \frac{1}{2} x + \frac{1}{2}$ .

Найдем точки пересечения прямой $y = \frac{1}{2} x + \frac{1}{2}$ с осями координат, точки $A$ и $B$ (рис. 5). Для точки $A$ , точки пересечения с осью абсцисс, ордината равна $0$ , тогда

$0 = \frac{1}{2} x + \frac{1}{2}$ ,

$x = - 1$ .

То есть у точки $A$ координаты $(- 1; 0)$ . Аналогично рассуждая (только теперь абсцисса равна $0$ ), получим координаты точки $B$ : $B (0; \frac{1}{2})$ .

Рассмотрим прямоугольный треугольник $A O B$ (рис. 5). Проведем $O H ⊥ A B$ ,
$O H$ — искомое расстояние.

По формуле нахождения расстояния между двумя точками:

$A B = \sqrt{{(- 1 - 0)}^{2} + {(0 - \frac{1}{2})}^{2}} = \frac{\sqrt{5}}{2}$ .

Площадь треугольника $A O B$ равна половине произведения $A B$ и $O H$ , но, с другой стороны, она же равна и половине произведения катетов $O A$ и $O B$ . Тогда имеем равенство

$O A \cdot O B = A B \cdot O H$ ,

откуда $O H = \frac{O A \cdot O B}{A B}$ , т. е. $O H = \frac{1}{\sqrt{5}}$ .

Ответ: $\frac{1}{\sqrt{5}}$ .

Упражнение 2

1. Записать уравнение касательной к графику функции $y = f (x)$ в точке с абсциссой $x_{0} = 0$ :

а) $f (x) = \sqrt{x + 9}$ ; б) $f (x) = \cos \frac{x}{4}$ .

2. Найти точки графика функции $f (x) = x^{3} + 3 x^{2}$ , в которых касательная к нему параллельна оси абсцисс.

Контрольные вопросы

1. Запишите уравнение касательной к графику функции $y = f (x), x \in A$ в точке $a \in A$ .

2. К графику функции $y = 4 x^{3} - x^{2} + 2 x + 3$ в точке с абсциссой $x = 1$ проведена касательная. Какой из прямых $y = 10 x - 3$ , $y = 12 x + 1$ , $y = 2 - 12 x$ , $y = 4 - 10 x$ , $y = 5 + 12 x$ она параллельна?

Ответы

Упражнение 1

1. $arctg 4$ . 2. $arctg (2 \sqrt{2})$ .

Упражнение 2

1. а) $y = \frac{1}{6} x + 3$ ; б) $y = 1$ .

2. $(- 2; 4)$

Конспект урока: Геометрический смысл производной

Производная