- Свойства функции, непрерывной на отрезке
- Алгоритм отыскания наименьшего и наибольшего значений непрерывной функции на заданном отрезке
- Знать алгоритм отыскания наименьшего и наибольшего значений функции
- Уметь решать задачи на отыскание наибольших и наименьших значений функции
- Какие точки называют критическими?
- Какие точки называют стационарными?
- Что такое экстремумы функции?
Свойства функции, непрерывной на отрезке
 Рис. 1.
Рис. 1.
На практике довольно часто приходится вычислять наибольшее и наименьшее значения функции. Такие задачи решаются тогда, когда выясняют как минимизировать издержки, увеличить прибыль, оптимизировать производство и т.д., то есть в тех случаях, когда нужно определить оптимальное значение некоторого параметра. Решить задачу на нахождение наибольшего и наименьшего значений функции можно с помощью производной.
Чтобы понять как это сделать, проанализируем графики на рисунке 1 и сформулируем некоторые свойства функции, непрерывной на отрезке.
- Если функция непрерывна на отрезке, то она достигает на нём и своего наибольшего, и своего наименьшего значений.
- Наибольшего и наименьшего значений непрерывная функция может достигать как на концах отрезка, так и внутри него.
- Если наибольшее (или наименьшее) значение достигается внутри отрезка, то только в критической точке.
Из этих свойств и вытекает способ нахождения наибольшего и наименьшего значений функции, который мы сформулируем в виде алгоритма.
Алгоритм отыскания наименьшего и наибольшего значений непрерывной функции на заданном отрезке
- Найти производную функции.
- Найти критические точки, лежащие внутри отрезка .
- Вычислить значения функции в найденных критических точках (п. 2), и в точках и ; выбрать среди этих значений наименьшее и наибольшее .
Рассмотрим примеры решения задач на отыскание наименьшего и наибольшего значений функции.
Пример 1
Найти наибольшее и наименьшее значения функции на отрезке .
Решение:
Воспользуемся алгоритмом.
1. Найдём производную:
.
2. Производная существует при всех . Найдём точки, в которых производная равна нулю:
; .
3. Одна из этих стационарных точек () принадлежит заданному отрезку . Найдём значения функции на концах данного отрезка и в критической точке :
Осталось выбрать наименьшее и наибольшее значения.
Ответ: ; .
Пример 2
Найти наибольшее и наименьшее значения функции на отрезке .
Решение:
1. Найдём производную:
.
2. Найдём критические точки:
; .
3. Из найденных точек только принадлежит отрезку . Найдём значения функции на концах данного отрезка и в критической точке :
Ответ: ; .
Пример 3
Вокруг прямоугольного поля площадью , равной га должны быть посажены со всех сторон деревья в виде полосы шириной , равной м. Каковы должны быть линейные размеры поля, чтобы площадь, занимаемая деревьями, была наименьшей?
Решение
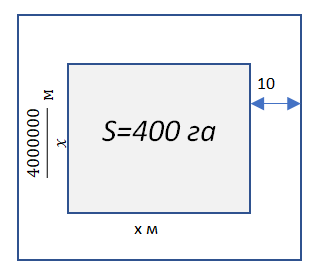 Рис. 2. Прямоугольное поле
Рис. 2. Прямоугольное поле
Обозначим одну из сторон прямоугольного поля переменной (рис. 2).
Площадь этого поля .
Значит, другая сторона поля равна .
Введём функцию , значение которой равно площади полосы деревьев вокруг поля.
.
После преобразований получим .
Найдём производную этой функции
.
Найдём стационарные точки.
(учитывая, что ).
 Рис. 3.
Рис. 3.
Данная точка является единственной точкой минимума (рис. 3). Поэтому в ней функция будет принимать наименьшее значение. Таким образом, одна из сторон поля равна 2000 м. Тогда и другая сторона равна .
Ответ: Поле должно иметь форму квадрата со стороной 2 км.
Иногда наибольшее и наименьшее значения функции нужно находить не на отрезке, а не интервале. Часто встречаются задачи, в которых функция имеет только одну стационарную точку на заданном интервале: точку максимума или точку минимума. Тогда в точке максимума функция принимает свое наибольшее значение на интервале, а в точке минимума – наименьшее значение.
Также при решении задач на нахождение наибольшего и наименьшего значений функции можно использовать следующее утверждение:
Если значения функции неотрицательны на некотором промежутке, то эта функция и функция , , принимают наибольшее (наименьшее) значение в одной и той же точке.
Упражнение
- Найдите наибольшее и наименьшее значения функции на отрезке .
- Найдите наибольшее и наименьшее значения функции на отрезке .
- Площадь, занимаемая печатным текстом, составляет на странице книги 363 см2. Ширина полей вверху и внизу страницы составляет по 2 см, а ширина боковых полей по 1,5 см. Каковы должны быть размеры каждой страницы, чтобы площадь её была наименьшей?
Контрольные вопросы
- Сформулируйте свойства непрерывной на отрезке функции.
- Сформулируйте алгоритм отыскания наименьшего и наибольшего значений непрерывной функции на заданном отрезке.
Упражнение
- 69 и -12;
- и 0;
- 26 см и 19,5 см.
