- Объем прямой призмы;
- Решение заданий.
- Знать формулу объёма прямой призмы;
- Уметь применять формулу объёма прямой призмы при решении задач.
- Что такое прямая призма?
- Чему равен объём прямоугольного параллелепипеда, рёбра которого равны 3, 7 и 11?
- Как найти объём прямой призмы, в основании которой лежит прямоугольный треугольник?
Объём прямой призмы
В основании призмы может лежать любой многоугольник. Призма, боковые ребра которой перпендикулярны основаниям, называется прямой призмой.
Теорема
Объем прямой призмы равен произведению площади основания на высоту, т.е. .
Чтобы доказать эту теорему, воспользуемся одним из свойств объёма: объем многогранника, составленного из нескольких тел, равен сумме объёмов этих многогранников, и формулой объёма прямой призмы, в основании которой лежит прямоугольный треугольник.
 Рис. 1. Прямая треугольная призма
Рис. 1. Прямая треугольная призма
Сначала рассмотрим треугольную прямую призму (рис. 1).
Построим сечение плоскостью таким образом, что и . Плоскость разделила призму на две прямые призмы и , в основаниях которых лежат прямоугольные треугольники и соответственно. Причём, высоты этих призм одинаковые, т.к. высота каждой призмы равна боковому ребру. Тогда
,
где треугольник - основание прямой треугольной призмы Таким образом, доказали, что площадь любой прямой треугольной призмы равна произведению площади основания на высоту.
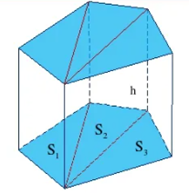 Рис. 2. Прямая призма
Рис. 2. Прямая призма
Теперь рассмотрим произвольную прямую призму
(рис. 2). Любую призму можно разбить на прямые треугольные призмы, высоты которых равны, а объёмы равны произведению площади основания на высоту. Тогда объём исходной прямой призмы равен сумме объёмов прямых треугольных призм, т.е.
.
Пример 1
Найдите объём правильной шестиугольной призмы (рис. 3), стороны основания которой равны 4, а боковые ребра равны .
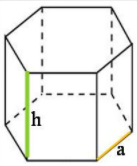 Рис. 3. Правильная шестиугольная призма
Рис. 3. Правильная шестиугольная призма
Решение
Правильная призма – это прямая призма, в основании которой лежит правильный многоугольник.
Воспользуемся формулой объёма прямой призмы , где - боковое ребро.
В основании призмы лежит правильный шестиугольник, площадь которого можно вычислить по формуле , где - длина стороны шестиугольника.
Тогда получим
.
Ответ: 24.
Пример 2
В сосуд, имеющий форму прямой треугольной призмы, налили 2600 см3 воды и полностью в неё погрузили деталь. При этом уровень жидкости в сосуде поднялся с отметки 50 см до 54 см. Чему равен объём детали? Ответ выразите в .
Решение
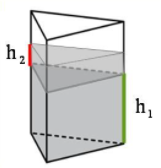 Рис. 4. Сосуд, имеющий форму прямой треугольной призмы
Рис. 4. Сосуд, имеющий форму прямой треугольной призмы
Пусть см, см.
Объём детали (рис. 4) равен объему вытесненной жидкости, т.е. .
Если исходный объём известен, то новый необходимо найти, воспользовавшись формулой объёма прямой призмы , так как вода налита в сосуд, имеющий форму прямой треугольной призмы.
Площадь основания выразим через исходный объём, получим
.
Тогда получим
.
Ответ: 208 см3.
Упражнение 1
1. Найдите объём правильной шестиугольной призмы, стороны основания которой равны 2, а боковые ребра равны .
2. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 180 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 3 раза больше, чем у первого? Ответ выразите в см.
Контрольные вопросы
1. Как найти объём прямой призмы?
2. Объясните, как можно получить формулу объёма прямой призмы.
Упражнение 1
1. 3. 2. 20 см.
- Объем прямой призмы;
- Решение заданий.
- Знать формулу объёма прямой призмы;
- Уметь применять формулу объёма прямой призмы при решении задач.
- Что такое прямая призма?
- Чему равен объём прямоугольного параллелепипеда, рёбра которого равны 3, 7 и 11?
- Как найти объём прямой призмы, в основании которой лежит прямоугольный треугольник?
Объём прямой призмы
В основании призмы может лежать любой многоугольник. Призма, боковые ребра которой перпендикулярны основаниям, называется прямой призмой.
Теорема
Объем прямой призмы равен произведению площади основания на высоту, т.е. .
Чтобы доказать эту теорему, воспользуемся одним из свойств объёма: объем многогранника, составленного из нескольких тел, равен сумме объёмов этих многогранников, и формулой объёма прямой призмы, в основании которой лежит прямоугольный треугольник.
 Рис. 1. Прямая треугольная призма
Рис. 1. Прямая треугольная призма
Сначала рассмотрим треугольную прямую призму (рис. 1).
Построим сечение плоскостью таким образом, что и . Плоскость разделила призму на две прямые призмы и , в основаниях которых лежат прямоугольные треугольники и соответственно. Причём, высоты этих призм одинаковые, т.к. высота каждой призмы равна боковому ребру. Тогда
,
где треугольник - основание прямой треугольной призмы Таким образом, доказали, что площадь любой прямой треугольной призмы равна произведению площади основания на высоту.
 Рис. 2. Прямая призма
Рис. 2. Прямая призма
Теперь рассмотрим произвольную прямую призму
(рис. 2). Любую призму можно разбить на прямые треугольные призмы, высоты которых равны, а объёмы равны произведению площади основания на высоту. Тогда объём исходной прямой призмы равен сумме объёмов прямых треугольных призм, т.е.
.
Пример 1
Найдите объём правильной шестиугольной призмы (рис. 3), стороны основания которой равны 4, а боковые ребра равны .
 Рис. 3. Правильная шестиугольная призма
Рис. 3. Правильная шестиугольная призма
Решение
Правильная призма – это прямая призма, в основании которой лежит правильный многоугольник.
Воспользуемся формулой объёма прямой призмы , где - боковое ребро.
В основании призмы лежит правильный шестиугольник, площадь которого можно вычислить по формуле , где - длина стороны шестиугольника.
Тогда получим
.
Ответ: 24.
Пример 2
В сосуд, имеющий форму прямой треугольной призмы, налили 2600 см3 воды и полностью в неё погрузили деталь. При этом уровень жидкости в сосуде поднялся с отметки 50 см до 54 см. Чему равен объём детали? Ответ выразите в .
Решение
 Рис. 4. Сосуд, имеющий форму прямой треугольной призмы
Рис. 4. Сосуд, имеющий форму прямой треугольной призмы
Пусть см, см.
Объём детали (рис. 4) равен объему вытесненной жидкости, т.е. .
Если исходный объём известен, то новый необходимо найти, воспользовавшись формулой объёма прямой призмы , так как вода налита в сосуд, имеющий форму прямой треугольной призмы.
Площадь основания выразим через исходный объём, получим
.
Тогда получим
.
Ответ: 208 см3.
Упражнение 1
1. Найдите объём правильной шестиугольной призмы, стороны основания которой равны 2, а боковые ребра равны .
2. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 180 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 3 раза больше, чем у первого? Ответ выразите в см.
Контрольные вопросы
1. Как найти объём прямой призмы?
2. Объясните, как можно получить формулу объёма прямой призмы.
Упражнение 1
1. 3. 2. 20 см.


