- Вычисление объёмов тел с помощью определённого интеграла.
- Знать и уметь выводить основную (общую) формулу для вычисления объёмов тел;
- Уметь использовать интеграл для вычисления объёмов различных тел.
- Чему равен объём прямоугольного параллелепипеда, прямой призмы, цилиндра?
- Как с помощью интеграла вычислить площадь криволинейной трапеции?
Вычисление объёмов тел с помощью определённого интеграла
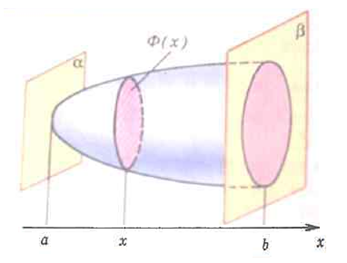 Рис. 1.
Рис. 1.
Одним из приложений определённого интеграла, который вы изучали в курсе алгебры, является вычисление объёмов тел. Пусть некоторое тело заключено между параллельными плоскостями и (рис. 1).
Введём систему координат таким образом, чтобы ось была перпендикулярна к плоскостям и .
Введём следующие обозначения:
и – абсциссы точек пересечения плоскостей и с осью соответственно ;
– сечение тела плоскостью, перпендикулярной к оси и проходящей через точку с абсциссой , ;
– площадь фигуры .
Будем считать, что тело такое, что является либо кругом, либо многоугольником при любом из отрезка (если и , то сечение – точка) и является непрерывной функцией на отрезке .
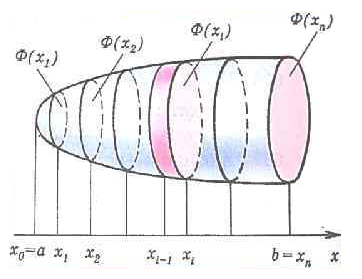 Рис. 2.
Рис. 2.
Отметим точки , разбивающие отрезок на равных отрезков. Через точки проведём плоскости, перпендикулярные к оси (рис. 2). Проведённые плоскости разбивают тело на тел: .
Объём тела приближённо равен , где .
Объём всего тела можно приближённо вычислить по формуле
.
Чем больше (чем меньше ), тем точнее приближённое значение , а при (при ) , т.е. . При этом является интегральной суммой для непрерывной функции на числовом отрезке . Следовательно, .
Таким образом, мы получаем основную формулу для вычисления объёмов тел с помощью интеграла:
Рассмотрим примеры нахождения объёмов тел с помощью интеграла.
Пример 1
Найдите объём конуса, радиус основания которого равен 2, а высота равна 1.
Решение
Чтобы было удобно использовать определённый интеграл, расположим конус таким образом, чтобы ось конуса была параллельна координатной оси , а проекция вершины конуса на ось была равна нулю (рис. 3).
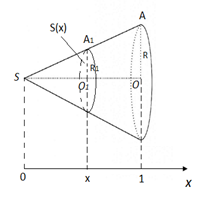 Рис. 3.
Рис. 3.
Рассмотрим сечение конуса плоскостью, перпендикулярной оси и выразим площадь этого сечения как функцию от .
Из подобия треугольников и следует .
Получили . Подставим в основную формулу объёма тела.
.
Ответ: .
Пример 2
Найдите объём тела, полученного путём вращения вокруг оси криволинейной трапеции, ограниченной линиями , , , .
Решение
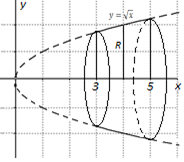 Рис. 4.
Рис. 4.
Так как рассматриваемое тело является телом вращения, то любое сечение плоскостью перпендикулярной оси вращения – круг. При этом радиус равен значению функции в точке , т.е. .
Вычислим объём данного тела с помощью интеграла .
.
Ответ: .
Если тело вращения получено вращением графика функции вокруг оси и ограничено плоскостями , , то его объем может быть вычислен по формуле:
Если тело вращения получено вращением графика функции вокруг оси и ограничено плоскостями , , то его объем может быть вычислен по формуле: .
Из основной формулы вычисления объемов тел следует, что отношение объёмов подобных тел равно кубу коэффициента подобия.
Пример 3
Фигура, заштрихованная на рисунке 5, вращается вокруг оси . Найдите объем полученного тела вращения.
Решение
 Рис. 5
Рис. 5
Для того, чтобы воспользоваться формулой вычисления объема тела, полученного вращением графика функции вокруг оси , преобразуем функцию к виду .
,
,
,
.
Тогда
.
Ответ: .
Упражнение 1
1. Вычислите объём тела, полученного вращением вокруг оси фигуры, ограниченной линиями .
2. Вычислите объём тела, полученного вращением вокруг оси фигуры, ограниченной линиями .
3. Вычислите объём тела, полученного вращением вокруг оси фигуры, ограниченной линиями .
4. Выведите формулу для вычисления объёма тела вращения с помощью определённого интеграла.
Контрольные вопросы
1. Что является сечением тел вращения плоскостью, перпендикулярной оси тела вращения?
2. Запишите основную формулу вычисления объёма тела с помощью определённого интеграла.
Упражнение 1
1. ;
2. ;
3. .
- Вычисление объёмов тел с помощью определённого интеграла.
- Знать и уметь выводить основную (общую) формулу для вычисления объёмов тел;
- Уметь использовать интеграл для вычисления объёмов различных тел.
- Чему равен объём прямоугольного параллелепипеда, прямой призмы, цилиндра?
- Как с помощью интеграла вычислить площадь криволинейной трапеции?
Вычисление объёмов тел с помощью определённого интеграла
 Рис. 1.
Рис. 1.
Одним из приложений определённого интеграла, который вы изучали в курсе алгебры, является вычисление объёмов тел. Пусть некоторое тело заключено между параллельными плоскостями и (рис. 1).
Введём систему координат таким образом, чтобы ось была перпендикулярна к плоскостям и .
Введём следующие обозначения:
и – абсциссы точек пересечения плоскостей и с осью соответственно ;
– сечение тела плоскостью, перпендикулярной к оси и проходящей через точку с абсциссой , ;
– площадь фигуры .
Будем считать, что тело такое, что является либо кругом, либо многоугольником при любом из отрезка (если и , то сечение – точка) и является непрерывной функцией на отрезке .
 Рис. 2.
Рис. 2.
Отметим точки , разбивающие отрезок на равных отрезков. Через точки проведём плоскости, перпендикулярные к оси (рис. 2). Проведённые плоскости разбивают тело на тел: .
Объём тела приближённо равен , где .
Объём всего тела можно приближённо вычислить по формуле
.
Чем больше (чем меньше ), тем точнее приближённое значение , а при (при ) , т.е. . При этом является интегральной суммой для непрерывной функции на числовом отрезке . Следовательно, .
Таким образом, мы получаем основную формулу для вычисления объёмов тел с помощью интеграла:
Рассмотрим примеры нахождения объёмов тел с помощью интеграла.
Пример 1
Найдите объём конуса, радиус основания которого равен 2, а высота равна 1.
Решение
Чтобы было удобно использовать определённый интеграл, расположим конус таким образом, чтобы ось конуса была параллельна координатной оси , а проекция вершины конуса на ось была равна нулю (рис. 3).
 Рис. 3.
Рис. 3.
Рассмотрим сечение конуса плоскостью, перпендикулярной оси и выразим площадь этого сечения как функцию от .
Из подобия треугольников и следует .
Получили . Подставим в основную формулу объёма тела.
.
Ответ: .
Пример 2
Найдите объём тела, полученного путём вращения вокруг оси криволинейной трапеции, ограниченной линиями , , , .
Решение
 Рис. 4.
Рис. 4.
Так как рассматриваемое тело является телом вращения, то любое сечение плоскостью перпендикулярной оси вращения – круг. При этом радиус равен значению функции в точке , т.е. .
Вычислим объём данного тела с помощью интеграла .
.
Ответ: .
Если тело вращения получено вращением графика функции вокруг оси и ограничено плоскостями , , то его объем может быть вычислен по формуле:
Если тело вращения получено вращением графика функции вокруг оси и ограничено плоскостями , , то его объем может быть вычислен по формуле: .
Из основной формулы вычисления объемов тел следует, что отношение объёмов подобных тел равно кубу коэффициента подобия.
Пример 3
Фигура, заштрихованная на рисунке 5, вращается вокруг оси . Найдите объем полученного тела вращения.
Решение
 Рис. 5
Рис. 5
Для того, чтобы воспользоваться формулой вычисления объема тела, полученного вращением графика функции вокруг оси , преобразуем функцию к виду .
,
,
,
.
Тогда
.
Ответ: .
Упражнение 1
1. Вычислите объём тела, полученного вращением вокруг оси фигуры, ограниченной линиями .
2. Вычислите объём тела, полученного вращением вокруг оси фигуры, ограниченной линиями .
3. Вычислите объём тела, полученного вращением вокруг оси фигуры, ограниченной линиями .
4. Выведите формулу для вычисления объёма тела вращения с помощью определённого интеграла.
Контрольные вопросы
1. Что является сечением тел вращения плоскостью, перпендикулярной оси тела вращения?
2. Запишите основную формулу вычисления объёма тела с помощью определённого интеграла.
Упражнение 1
1. ;
2. ;
3. .


