- Понятие объёма;
- Объём прямоугольного параллелепипеда;
- Следствия из теоремы об объёме прямоугольного параллелепипеда.
- Знать свойства объёмов;
- Знать формулу объёма прямоугольного параллелепипеда;
- Уметь вычислять объем прямоугольного параллелепипеда;
- Знать следствия из теоремы об объёме прямоугольного параллелепипеда;
- Уметь пользоваться следствиями для решения задач.
- Что такое прямоугольный параллелепипед?
- Какими свойствами обладает прямоугольный параллелепипед?
- Что такое площадь фигуры?
Понятие объёма
Еще в глубокой древности у людей возникла необходимость в измерении количества различных веществ. Сыпучие вещества и жидкости можно было мерить, наполняя ими сосуды определенной вместимости, т.е. определяя их количество по объему.
Понятие объема в стереометрии вводится аналогично понятию площади в планиметрии. В планиметрии мы определяли площадь так: площадь многоугольника – это величина той части плоскости, которую занимает многоугольник.
Аналогично можно сформулировать понятие объёма тела.
Величина части пространства, занимаемого геометрическим телом, называется объёмом этого тела.
Единицы измерения объёма тоже определяются аналогично единицам измерения площади. За единицу измерения объёмов приняли куб, ребро которого равно единице измерения отрезков.
Куб с ребром 1 см (1 м, 1 дм, 1 мм и т.д.) называют кубическим сантиметром (метром, дециметром или миллиметром) и обозначают (, или ).
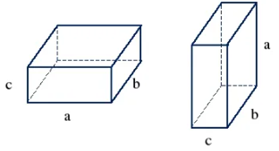 Рис. 1. Два равных прямоугольных параллелепипеда
Рис. 1. Два равных прямоугольных параллелепипеда
Вспомним, что в планиметрии две фигуры назывались равными, если их можно совместить наложением. Аналогично, два тела называются равными, если их можно совместить наложением.
На рисунке 1 изображены два равных прямоугольных параллелепипеда с равными измерениями.
 Рис. 2. Тело, составленное из цилиндра и конуса
Рис. 2. Тело, составленное из цилиндра и конуса
Равные фигуры в планиметрии имели равные площади, значит, можем сказать, что равные тела имеют равные объёмы.
Ещё знаем, что если фигура в планиметрии составлена из нескольких фигур, то её площадь равна сумме площадей этих фигур. Аналогичным свойством обладает и объём.
На рисунке 2 тело состоит из конуса и цилиндра, значит его объём равен сумме объёмов этих двух тел.
Таким образом, получили основные свойства объемов.
Свойства объемов.
1. Равные тела имеют равные объемы.
2. Если тело составлено из нескольких тел, то его объем равен сумме объемов этих тел.
Объём прямоугольного параллелепипеда
Формула объёма прямоугольного параллелепипеда известна ещё с 5 класса:
,
где , и – измерения прямоугольного параллелепипеда. А вообще существует специальная теорема.
Теорема
Объём прямоугольного параллелепипеда равен произведению трёх его измерений.
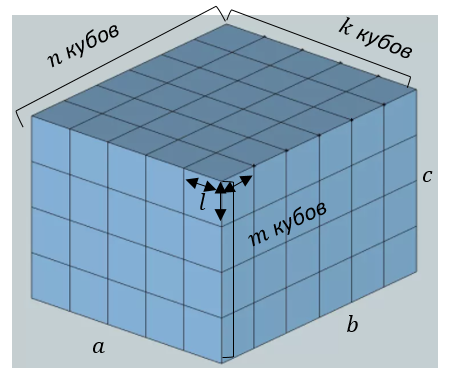 Рис. 3. Объём прямоугольного параллелепипеда
Рис. 3. Объём прямоугольного параллелепипеда
Теорему легко доказать, если разбить прямоугольный параллелепипед на целое число кубов (рис. 3). Ребро куба можно подобрать так, чтобы в каждое измерение прямоугольного параллелепипеда укладывалось целое число ребер куба, т.е. , где , и – целые числа. Объём каждого из них есть элементарный объём, принятый за единицу измерения или . Тогда объем самого прямоугольного параллелепипеда будет суммой объемов всех кубов:
или
.
Пример 1
Найдите объем многогранника, изображенного на рисунке 4 (все двугранные углы многогранника прямые).
Решение
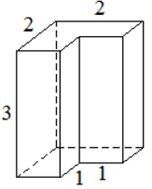 Рис. 4. Многогранник
Рис. 4. Многогранник
Данный многогранник получили из прямоугольного параллелепипеда с измерениями 2, 2 и 3, вырезав из правого переднего угла прямоугольный параллелепипед с измерениями 1, 1 и 3.
Объём каждого из этих параллелепипедов можно найти по формуле . Получим
,
.
Тогда объём многогранника можем найти как разность объемов
.
Ответ: 9.
Упражнение 1
Найдите объем многогранников, изображенных на рисунке 5 (все двугранные углы многогранника прямые).
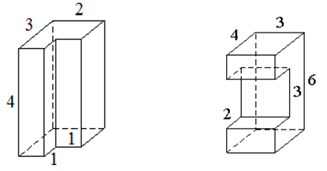 Рис. 5. Многогранники
Рис. 5. Многогранники
Следствия из теоремы об объёме прямоугольного параллелепипеда
Рассмотрим важные следствия из теоремы об объёме прямоугольного параллелепипеда.
Следствие 1
Объём прямоугольного параллелепипеда равен произведению площади основания на высоту, т.е.
.
Докажем следствие.
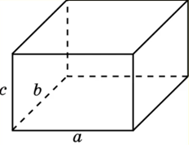 Рис. 6. Прямоугольный параллелепипед
Рис. 6. Прямоугольный параллелепипед
Рассмотрим прямоугольный параллелепипед с измерениями и (рис. 6).
Пусть грань, ребра которой равны и , будет основанием. Тогда площадь основания равна , так как грань является прямоугольником.
Ребро является высотой параллелепипеда, т.к. он прямоугольный, т.е. .
По теореме об объёме прямоугольного параллелепипеда
.
Следствие 2
Объём прямой призмы, основанием которой является прямоугольный треугольник, равен произведению площади основания на высоту, т.е.
 Рис. 7.
Рис. 7.
Рассмотрим доказательство этого следствия.
Опять будем работать с прямоугольным параллелепипедом . Знаем из следствия 1, что Площадь основания для этого прямоугольного параллелепипеда равна площади прямоугольника .
Проведем диагональное сечение . Эта плоскость разделила прямоугольный параллелепипед на две равные прямые призмы, в основании каждой из которых прямоугольный треугольник. Значит, объём каждой призмы в 2 раза меньше объёма прямоугольного параллелепипеда.
Тогда
.
При этом диагональ делит прямоугольник на два прямоугольных треугольника таких, что . Следовательно, формула объема призмы имеет вид:
.
Пример 2
Основанием прямой треугольной призмы является прямоугольный треугольник с катетами 2 и 7, боковое ребро призмы равно 6. Найдите объём призмы.
Решение
Используем формулу из следствия 2: , где площадь основания – это площадь прямоугольного треугольника, т.е. получим
.
Ответ: 42.
Упражнение 2
1. Основанием прямой треугольной призмы является прямоугольный треугольник с катетами 3 и 4, боковое ребро призмы равно 4. Найдите объём призмы.
2. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 4 и 7, объём призмы равен 56. Найдите боковое ребро призмы.
Контрольные вопросы
1. Какими свойствами обладает объём?
2. Какие единицы измерения объёма есть?
3. Как найти объём прямоугольного параллелепипеда?
Упражнение 1
- 20. 2. 54.
Упражнение 2
1. 24. 2. 4.
- Понятие объёма;
- Объём прямоугольного параллелепипеда;
- Следствия из теоремы об объёме прямоугольного параллелепипеда.
- Знать свойства объёмов;
- Знать формулу объёма прямоугольного параллелепипеда;
- Уметь вычислять объем прямоугольного параллелепипеда;
- Знать следствия из теоремы об объёме прямоугольного параллелепипеда;
- Уметь пользоваться следствиями для решения задач.
- Что такое прямоугольный параллелепипед?
- Какими свойствами обладает прямоугольный параллелепипед?
- Что такое площадь фигуры?
Понятие объёма
Еще в глубокой древности у людей возникла необходимость в измерении количества различных веществ. Сыпучие вещества и жидкости можно было мерить, наполняя ими сосуды определенной вместимости, т.е. определяя их количество по объему.
Понятие объема в стереометрии вводится аналогично понятию площади в планиметрии. В планиметрии мы определяли площадь так: площадь многоугольника – это величина той части плоскости, которую занимает многоугольник.
Аналогично можно сформулировать понятие объёма тела.
Величина части пространства, занимаемого геометрическим телом, называется объёмом этого тела.
Единицы измерения объёма тоже определяются аналогично единицам измерения площади. За единицу измерения объёмов приняли куб, ребро которого равно единице измерения отрезков.
Куб с ребром 1 см (1 м, 1 дм, 1 мм и т.д.) называют кубическим сантиметром (метром, дециметром или миллиметром) и обозначают (, или ).
 Рис. 1. Два равных прямоугольных параллелепипеда
Рис. 1. Два равных прямоугольных параллелепипеда
Вспомним, что в планиметрии две фигуры назывались равными, если их можно совместить наложением. Аналогично, два тела называются равными, если их можно совместить наложением.
На рисунке 1 изображены два равных прямоугольных параллелепипеда с равными измерениями.
 Рис. 2. Тело, составленное из цилиндра и конуса
Рис. 2. Тело, составленное из цилиндра и конуса
Равные фигуры в планиметрии имели равные площади, значит, можем сказать, что равные тела имеют равные объёмы.
Ещё знаем, что если фигура в планиметрии составлена из нескольких фигур, то её площадь равна сумме площадей этих фигур. Аналогичным свойством обладает и объём.
На рисунке 2 тело состоит из конуса и цилиндра, значит его объём равен сумме объёмов этих двух тел.
Таким образом, получили основные свойства объемов.
Свойства объемов.
1. Равные тела имеют равные объемы.
2. Если тело составлено из нескольких тел, то его объем равен сумме объемов этих тел.
Объём прямоугольного параллелепипеда
Формула объёма прямоугольного параллелепипеда известна ещё с 5 класса:
,
где , и – измерения прямоугольного параллелепипеда. А вообще существует специальная теорема.
Теорема
Объём прямоугольного параллелепипеда равен произведению трёх его измерений.
 Рис. 3. Объём прямоугольного параллелепипеда
Рис. 3. Объём прямоугольного параллелепипеда
Теорему легко доказать, если разбить прямоугольный параллелепипед на целое число кубов (рис. 3). Ребро куба можно подобрать так, чтобы в каждое измерение прямоугольного параллелепипеда укладывалось целое число ребер куба, т.е. , где , и – целые числа. Объём каждого из них есть элементарный объём, принятый за единицу измерения или . Тогда объем самого прямоугольного параллелепипеда будет суммой объемов всех кубов:
или
.
Пример 1
Найдите объем многогранника, изображенного на рисунке 4 (все двугранные углы многогранника прямые).
Решение
 Рис. 4. Многогранник
Рис. 4. Многогранник
Данный многогранник получили из прямоугольного параллелепипеда с измерениями 2, 2 и 3, вырезав из правого переднего угла прямоугольный параллелепипед с измерениями 1, 1 и 3.
Объём каждого из этих параллелепипедов можно найти по формуле . Получим
,
.
Тогда объём многогранника можем найти как разность объемов
.
Ответ: 9.
Упражнение 1
Найдите объем многогранников, изображенных на рисунке 5 (все двугранные углы многогранника прямые).
 Рис. 5. Многогранники
Рис. 5. Многогранники
Следствия из теоремы об объёме прямоугольного параллелепипеда
Рассмотрим важные следствия из теоремы об объёме прямоугольного параллелепипеда.
Следствие 1
Объём прямоугольного параллелепипеда равен произведению площади основания на высоту, т.е.
.
Докажем следствие.
 Рис. 6. Прямоугольный параллелепипед
Рис. 6. Прямоугольный параллелепипед
Рассмотрим прямоугольный параллелепипед с измерениями и (рис. 6).
Пусть грань, ребра которой равны и , будет основанием. Тогда площадь основания равна , так как грань является прямоугольником.
Ребро является высотой параллелепипеда, т.к. он прямоугольный, т.е. .
По теореме об объёме прямоугольного параллелепипеда
.
Следствие 2
Объём прямой призмы, основанием которой является прямоугольный треугольник, равен произведению площади основания на высоту, т.е.
 Рис. 7.
Рис. 7.
Рассмотрим доказательство этого следствия.
Опять будем работать с прямоугольным параллелепипедом . Знаем из следствия 1, что Площадь основания для этого прямоугольного параллелепипеда равна площади прямоугольника .
Проведем диагональное сечение . Эта плоскость разделила прямоугольный параллелепипед на две равные прямые призмы, в основании каждой из которых прямоугольный треугольник. Значит, объём каждой призмы в 2 раза меньше объёма прямоугольного параллелепипеда.
Тогда
.
При этом диагональ делит прямоугольник на два прямоугольных треугольника таких, что . Следовательно, формула объема призмы имеет вид:
.
Пример 2
Основанием прямой треугольной призмы является прямоугольный треугольник с катетами 2 и 7, боковое ребро призмы равно 6. Найдите объём призмы.
Решение
Используем формулу из следствия 2: , где площадь основания – это площадь прямоугольного треугольника, т.е. получим
.
Ответ: 42.
Упражнение 2
1. Основанием прямой треугольной призмы является прямоугольный треугольник с катетами 3 и 4, боковое ребро призмы равно 4. Найдите объём призмы.
2. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 4 и 7, объём призмы равен 56. Найдите боковое ребро призмы.
Контрольные вопросы
1. Какими свойствами обладает объём?
2. Какие единицы измерения объёма есть?
3. Как найти объём прямоугольного параллелепипеда?
Упражнение 1
- 20. 2. 54.
Упражнение 2
1. 24. 2. 4.


