- Понятие вектора;
- Равенство векторов.
- Знать, что такое вектор: нулевой вектор, длина вектора;
- Знать, какие векторы называются коллинеарными, сонаправленными, противоположно направленными и равными;
- Уметь откладывать вектор, равный данному, от произвольной точки, находить длину вектора, определять сонаправленные, противоположно направленные, равные векторы.
- Какие прямые называются параллельными?
- Какие отрезки называются параллельными?
- Какие отрезки называются равными?
Понятие вектора
Понятие вектора в пространстве не отличается от понятия вектора на плоскости.
Отрезок, для которого указано, какой из его концов считается началом, а какой – концом, называется вектором .
Частным случаем вектора можно считать точку. Такой вектор называется нулевым . Начало и конец нулевого вектора совпадают. Поэтому такой вектор не имеет какого-то определённого направления.
Во всех остальных случаях (когда начало и конец вектора не совпадают) вектором является направленный отрезок. При изображении ненулевого вектора, его направление отмечается стрелкой (от начала к концу).
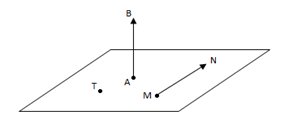 Рис. 1. Векторы в пространстве
Рис. 1. Векторы в пространстве
На рисунке 1 изображены ненулевые векторы и , а также нулевой вектор . Для обозначения нулевого вектора используют символ . Таким образом, .
Длиной или модулем ненулевого вектора называется длина отрезка . Длина вектора (вектора ) обозначается следующим образом: .
Длина нулевого вектора считается равной нулю .
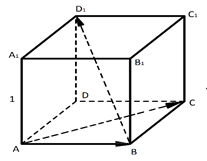 Рис. 2. К определению 2
Рис. 2. К определению 2
Пусть ребро куба равно 1 (рис. 2). Тогда, из определения длины вектора, можем записать:
;
;
.
Два ненулевых вектора называются коллинеарными , если они лежат на одной прямой или на параллельных прямых.
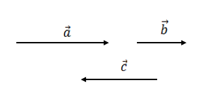 Рис. 3. Коллинеарные векторы
Рис. 3. Коллинеарные векторы
На рисунке 3 изображены коллинеарные векторы , , . Обозначается это так же как и параллельность прямых: .
Если два ненулевых вектора и коллинеарны, то они могут быть направлены либо в одну сторону, либо противоположно. В первом случае векторы и называются сонаправленными , а во втором – противоположно направленными . Сонаправленные векторы и записывают следующим образом: . Если же векторы и противоположно направлены, то записывают .
На рисунке 3 , , .
Многие физические величины являются векторными, т.е. имеют направление. К таким величинам относятся, например, перемещение, скорость, ускорение, сила, напряжённость электрического поля, магнитная индукция т.д. Поэтому изучение векторов и операций над ними имеет большое практическое значение для физики, астрономии и различных технических дисциплин.
Упражнение 1
1. В прямоугольном параллелепипеде и – середины рёбер и соответственно. Запишите векторы с началом и концом в вершинах параллелепипеда, которые:
- сонаправлены с вектором ;
- противоположно направлены вектору .
2. Прямая не лежит в плоскости . Через прямую проходит плоскость , пересекающая плоскость по прямой . Точки и принадлежат прямой , а точки и прямой . При каком условии векторы и будут коллинеарными?
Равенство векторов
Векторы называются равными , если они сонаправлены и их длины равны.
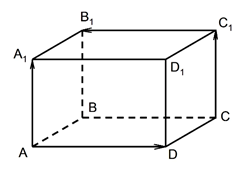 Рис. 4. Прямоугольный параллелепипед
Рис. 4. Прямоугольный параллелепипед
На рисунке 4 изображён параллелепипед.
На этом рисунке , .
При этом , так как они сонаправлены и имеют одинаковые длины, а векторы и не являются ни сонаправленными, ни противоположно направленными, так как они не коллинеарны.
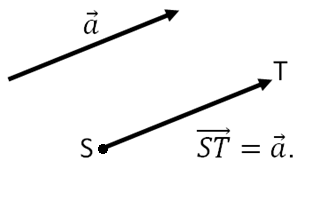 Рис. 5.
Рис. 5.
Если некоторая точка является началом некоторого вектора, то говорят, что данный вектор отложен от данной точки.
От любой точки можно отложить вектор, равный данному, и притом только один.
Действительно, пусть – данный вектор, – данная точка (рис. 5). Проведём через прямую, на которой лежит вектор , и точку плоскость и в этой плоскости построим . Вектор – искомый и при этом единственный вектор с началом , равный вектору .
Упражнение 2
1. Дан параллелепипед . Запишите векторы с началом и концом в вершинах параллелепипеда, равные векторам , , .
2. Точки , , , – середины рёбер соответственно , , , тетраэдра .
Из векторов выпишите все пары равных векторов.
Контрольные вопросы
- Что такое вектор?
- Что называют модулем вектора?
- Какой вектор называется нулевым?
- Какие векторы называются коллинеарными?
- Какие векторы называются сонаправленными?
- Какие векторы называются противоположно направленными?
- Какие векторы называются равными?
Упражнение 1
- 1) , ; 2) ,
- Если
Упражнение 2
- ; ;
- ; ;
