- Арктангенс числа.
- Формула решения простейшего тригонометрического уравнения .
- Арккотангенс числа.
- Формула решения простейшего тригонометрического уравнения .
- Вычисление значений тригонометрических выражений.
- Решение уравнений.
- Знать определение арктангенса и арккотангенса числа.
- Знать формулы решения уравнений и .
- Уметь решать простейшие тригонометрические уравнения типа и .
- Уметь вычислять значения тригонометрических выражений.
1. С помощью рис. 1 найти:
- все углы поворота точки А(1; 0) вокруг начала координат, чтобы получить точки В и С.
- все углы поворота точки А(1; 0) вокруг начала координат, чтобы получить точки D и E.
2. На рис. 2 изобразить
- точку С, соответствующую числу, синус которого равен .
- точку D, соответствующую числу, косинус которого равен .
- точку М, соответствующую числу, тангенс которого равен .
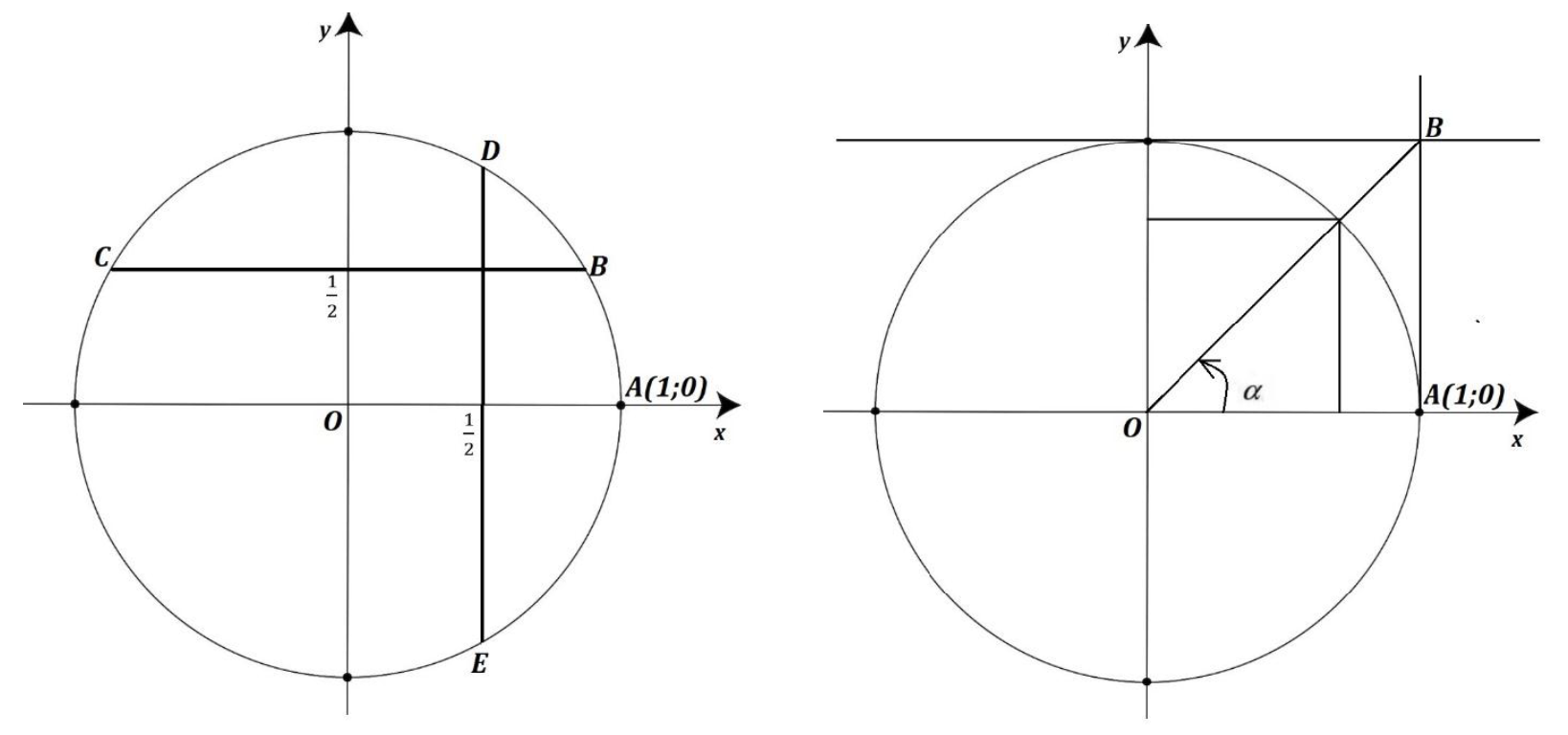 Рис. 1. Поворот точки вокруг начала координат Рис. 2. Точки единичной окружности
Рис. 1. Поворот точки вокруг начала координат Рис. 2. Точки единичной окружности
Решение простейшего тригонометрического уравнения
Рассмотрим следующий вид простейших тригонометрических уравнений, а именно .
По определению, тангенс угла — это отношение синуса угла к его косинусу. Отсюда следует, что может принимать любое действительное значение, тогда уравнение имеет корни при любом значении .
Пример 1
Решить уравнение
Решение
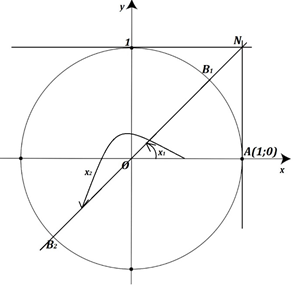 Рис. 3. Решение уравнения tg x = 1
Рис. 3. Решение уравнения tg x = 1
Через точку А(1; 0) проведем прямую, перпендикулярную АО (Рис. 3) и отложим на ней отрезок AN=1. Через точки N и О проведем прямую, она пересекает единичную окружность в двух точках В1 и В2, диаметрально противоположных друг другу. Найдем тангенс угла в прямоугольном треугольнике ANO. По определению, тангенс угла – отношение противолежащего катета к прилежащему, тогда откуда Значит, в точку В1 можно попасть при повороте точки А(1; 0) на угол а также на углы Точка В2 получается при повороте точки А на угол
а также на углы или, другими словами, Получили, что корни уравнения можно найти по формулам и а их, в свою очередь, можно объединить в одну
Ответ:
Пример 2
Решить уравнение
Решение
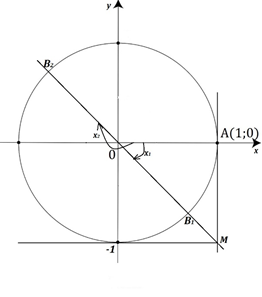 Рис. 4. Решение уравнения tg x = -1
Рис. 4. Решение уравнения tg x = -1
Пусть Прямая, проходящая через точки О и М пересекает единичную окружность в диаметрально противоположных точках В1 и В2. В прямоугольном треугольнике АОМ тогда Значит, в точку В1 можно попасть при повороте точки А(1; 0) на угол а также на углы Чтобы попасть в точку В2, нужно повернуть точку А(1; 0) на угол а также на углы Поэтому все корни уравнения можно найти по формуле
Ответ:
Из решений примеров 1 и 2 видно, что уравнения и имеют бесконечное множество корней. Но, заметим, что на у каждого уравнения только один корень. Для первого уравнения это число называют арктангенсом числа 1 (обозначают ); для второго — называют арктангенсом числа (обозначают ). Вообще говоря, уравнение , где имеет единственный корень на промежутке , причем, если то корень лежит на промежутке , если , то на промежутке и этот корень называется арктангенсом числа
Арктангенсом числа a, где , называется такое число тангенс которого равен :
, если и .
Для любого справедливо равенство
(1)
Равенство
(2)
верно только при .
Для любого верно равенство
(3)
Все корни уравнения , где , можно находить по формуле
. (4)
Пример 3
Вычислить:
а)
б)
в)
Решение
а) Так как , то — число из промежутка , тангенс которого равен Значит, Подставим найденные значения в исходное выражение:
б) Воспользуемся формулами приведения для каждого из слагаемых и применим формулу (1):
Подставим найденные значения в исходное выражение:
в) Пусть отсюда по определению арктангенса числа Тогда с новыми обозначениями нужно найти , где . C учетом того, что лежит в I или IV четверти, в которых косинус угла положительный, из формулы .
Ответ: а)
б) ;
в)
Упражнение 1
Вычислить:
1.
2.
3.
Уравнение . Арккотангенс числа
Следующий, последний, вид простейших тригонометрических уравнений, .
По определению, котангенс угла — это отношение косинуса угла к его синусу. Отсюда следует, что может принимать любое действительное значение, тогда уравнение имеет корни при любом значении .
Арккотангенсом числа a, где , называется такое число котангенс которого равен a:
, если и .
Для любого справедливо равенство
(5)
Равенство
(6)
верно только при
Для любого верно равенство
(7)
Все корни уравнения , где , можно находить по формуле
(8)
Пример 4
Вычислить:
а)
б)
Решение
а)
б)
Ответ: а)
б)
Упражнение 2
Вычислить:
1.
2.
Пример 5
Решить уравнение:
а)
б)
Решение
а) По формуле (4) находим откуда
б) Запишем исходное уравнение в виде тогда или По формуле (4) найдем корни этих уравнений. Для первого Для второго
Ответ: а)
б)
Упражнение 3
Решить уравнение:
1.
2.
Контрольные вопросы
1. С помощью единичной окружности решить уравнение
2. Покажите на единичной окружности точки, соответствующие корням уравнения .
3. Найдите решения уравнения на промежутке
Упражнение 1
1.
2.
3.
Упражнение 2
1.
2.
Упражнение 3
1.
2.
- Арктангенс числа.
- Формула решения простейшего тригонометрического уравнения .
- Арккотангенс числа.
- Формула решения простейшего тригонометрического уравнения .
- Вычисление значений тригонометрических выражений.
- Решение уравнений.
- Знать определение арктангенса и арккотангенса числа.
- Знать формулы решения уравнений и .
- Уметь решать простейшие тригонометрические уравнения типа и .
- Уметь вычислять значения тригонометрических выражений.
1. С помощью рис. 1 найти:
- все углы поворота точки А(1; 0) вокруг начала координат, чтобы получить точки В и С.
- все углы поворота точки А(1; 0) вокруг начала координат, чтобы получить точки D и E.
2. На рис. 2 изобразить
- точку С, соответствующую числу, синус которого равен .
- точку D, соответствующую числу, косинус которого равен .
- точку М, соответствующую числу, тангенс которого равен .
 Рис. 1. Поворот точки вокруг начала координат Рис. 2. Точки единичной окружности
Рис. 1. Поворот точки вокруг начала координат Рис. 2. Точки единичной окружности
Решение простейшего тригонометрического уравнения
Рассмотрим следующий вид простейших тригонометрических уравнений, а именно .
По определению, тангенс угла — это отношение синуса угла к его косинусу. Отсюда следует, что может принимать любое действительное значение, тогда уравнение имеет корни при любом значении .
Пример 1
Решить уравнение
Решение
 Рис. 3. Решение уравнения tg x = 1
Рис. 3. Решение уравнения tg x = 1
Через точку А(1; 0) проведем прямую, перпендикулярную АО (Рис. 3) и отложим на ней отрезок AN=1. Через точки N и О проведем прямую, она пересекает единичную окружность в двух точках В1 и В2, диаметрально противоположных друг другу. Найдем тангенс угла в прямоугольном треугольнике ANO. По определению, тангенс угла – отношение противолежащего катета к прилежащему, тогда откуда Значит, в точку В1 можно попасть при повороте точки А(1; 0) на угол а также на углы Точка В2 получается при повороте точки А на угол
а также на углы или, другими словами, Получили, что корни уравнения можно найти по формулам и а их, в свою очередь, можно объединить в одну
Ответ:
Пример 2
Решить уравнение
Решение
 Рис. 4. Решение уравнения tg x = -1
Рис. 4. Решение уравнения tg x = -1
Пусть Прямая, проходящая через точки О и М пересекает единичную окружность в диаметрально противоположных точках В1 и В2. В прямоугольном треугольнике АОМ тогда Значит, в точку В1 можно попасть при повороте точки А(1; 0) на угол а также на углы Чтобы попасть в точку В2, нужно повернуть точку А(1; 0) на угол а также на углы Поэтому все корни уравнения можно найти по формуле
Ответ:
Из решений примеров 1 и 2 видно, что уравнения и имеют бесконечное множество корней. Но, заметим, что на у каждого уравнения только один корень. Для первого уравнения это число называют арктангенсом числа 1 (обозначают ); для второго — называют арктангенсом числа (обозначают ). Вообще говоря, уравнение , где имеет единственный корень на промежутке , причем, если то корень лежит на промежутке , если , то на промежутке и этот корень называется арктангенсом числа
Арктангенсом числа a, где , называется такое число тангенс которого равен :
, если и .
Для любого справедливо равенство
(1)
Равенство
(2)
верно только при .
Для любого верно равенство
(3)
Все корни уравнения , где , можно находить по формуле
. (4)
Пример 3
Вычислить:
а)
б)
в)
Решение
а) Так как , то — число из промежутка , тангенс которого равен Значит, Подставим найденные значения в исходное выражение:
б) Воспользуемся формулами приведения для каждого из слагаемых и применим формулу (1):
Подставим найденные значения в исходное выражение:
в) Пусть отсюда по определению арктангенса числа Тогда с новыми обозначениями нужно найти , где . C учетом того, что лежит в I или IV четверти, в которых косинус угла положительный, из формулы .
Ответ: а)
б) ;
в)
Упражнение 1
Вычислить:
1.
2.
3.
Уравнение . Арккотангенс числа
Следующий, последний, вид простейших тригонометрических уравнений, .
По определению, котангенс угла — это отношение косинуса угла к его синусу. Отсюда следует, что может принимать любое действительное значение, тогда уравнение имеет корни при любом значении .
Арккотангенсом числа a, где , называется такое число котангенс которого равен a:
, если и .
Для любого справедливо равенство
(5)
Равенство
(6)
верно только при
Для любого верно равенство
(7)
Все корни уравнения , где , можно находить по формуле
(8)
Пример 4
Вычислить:
а)
б)
Решение
а)
б)
Ответ: а)
б)
Упражнение 2
Вычислить:
1.
2.
Пример 5
Решить уравнение:
а)
б)
Решение
а) По формуле (4) находим откуда
б) Запишем исходное уравнение в виде тогда или По формуле (4) найдем корни этих уравнений. Для первого Для второго
Ответ: а)
б)
Упражнение 3
Решить уравнение:
1.
2.
Контрольные вопросы
1. С помощью единичной окружности решить уравнение
2. Покажите на единичной окружности точки, соответствующие корням уравнения .
3. Найдите решения уравнения на промежутке
Упражнение 1
1.
2.
3.
Упражнение 2
1.
2.
Упражнение 3
1.
2.



