- Решение простейших тригонометрических неравенств на конкретных примерах.
- Решение тригонометрических уравнений, содержащих ограничения по ОДЗ.
- Знать алгоритм решения простейших тригонометрических неравенств.
- Знать вид тригонометрических уравнений, содержащих ограничения по ОДЗ.
- Уметь решать простейшие тригонометрические неравенства.
- Уметь решать тригонометрические уравнения с ограничениями по ОДЗ.
Решить уравнение:
1.
2.
3.
В предыдущих параграфах мы рассматривали различные типы тригонометрических уравнений. Все они, в конечном итоге, сводятся к решению простейших тригонометрических уравнений. Есть еще один тип тригонометрических уравнений, в которых есть ограничения по ОДЗ. Напомним, что областью допустимых значений выражения называются такие значения переменных, при которых выражение имеет смысл.
Но для начала познакомимся с тригонометрическими неравнествами.
Простейшие тригонометрические неравенства
Неравенство, в котором неизвестная переменная находится под знаком синуса, косинуса, тангенса или котангенса, называется тригонометрическим неравенством.
К простейшим тригонометрическим неравенствам относятся неравенства вида (вместо знака может быть любой из ). Здесь является неизвестным,
Пример 1
Решить неравенство
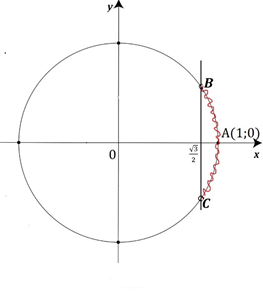 Рис. 1. Графическая интерпретация неравенства 1
Рис. 1. Графическая интерпретация неравенства 1
Решение
Косинус угла — абсцисса точки единичной окружности, полученной при повороте точки (1; 0) на угол . У двух точек В и С единичной окружности абсциссы равны (Рис. 1). Для того, чтобы получить точку В, нужно повернуть А(1; 0) на углы точку С — на углы У всех точек дуги единичной окружности, лежащей правее прямой ВС, абсциссы больше, чем . Тогда решением исходного неравенства является дуга СВ, значит,
Ответ:
Пример 2
Решить неравенство
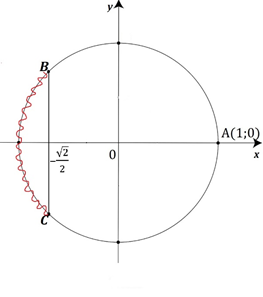 Рис. 2. Графическая интерпретация неравенства 2
Рис. 2. Графическая интерпретация неравенства 2
Решение
Пусть Решим неравенство Решением этого неравенства будут все точки дуги ВС (Рис. 2), т. е. Вернемся к исходной переменной:
Отсюда и
Ответ:
Пример 3
Решить неравенство
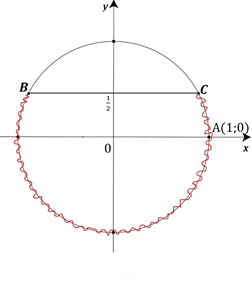 Рис. 3. Графическая интерпретация неравенства 3
Рис. 3. Графическая интерпретация неравенства 3
Решение
По определению синус угла — это ордината точки, полученной при повороте точки А(1; 0) на этот угол. Две точки окружности В и С имеют ординаты, равные (Рис. 3). Точка В получена поворотом точки А на угол или на углы Точка С — на углы Решением исходного неравенства являются все точки окружности, лежащие ниже прямой ВС, т. к. они все имеют ординаты, меньшие . Тогда решение неравенства — интервалы
Ответ:
Пример 4
Решить неравенство
Решение
К левой части неравенства применим формулы косинуса двойного угла и следствие из основного тригонометрического тождества, перенесем слагаемое из правой части неравенства в левую:
Пусть тогда неравенство примет вид:
откуда или
Вернемся к исходной переменной:
или Первое неравенство решений не имеет, т. к. решение второго —
Ответ:
Упражнение 1
Решить неравенство:
1.
2.
3.
Пример 5
Решить уравнение
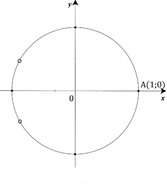 Рис. 4. Область допустимых значений выражения из примера 5
Рис. 4. Область допустимых значений выражения из примера 5
Решение
Левая часть уравнения — дробное выражение, а дробь имеет смысл тогда,
когда знаменатель отличен от нуля. Тогда ОДЗ: , ,
«Выколем» эти точки на числовой окружности (Рис. 4).
Приравняем к нулю числитель левой части: , , откуда или Видим, что второе множество решений не удовлетворяет ОДЗ уравнения, тогда решением является
Ответ:
Пример 6
Решить уравнение
Решение
По определению котангенс угла — отношение косинуса угла к его синусу, тогда левая часть равенства имеет смысл в каждой точке окружности, кроме тех, в которых т. е. ОДЗ:
Раскроем скобки в левой части уравнения, применив определение котангенса, следствие из основного тригонометрического тождества, перенесем слагаемое из правой части в левую:
Пусть тогда уравнение примет вид: откуда Вернемся к исходной переменной: Решением первого уравнения является второго — С учетом ОДЗ уравнения решение —
Ответ:
Упражнение 2
Решить уравнение:
1.
2.
Контрольные вопросы
- Опишите алгоритм решения простейшего тригонометрического неравенства.
- При каких значениях переменной имеет смысл дробное выражение? Арифметический квадратный корень? Логарифмическое выражение?
Упражнение 1
1.
2.
3.
Упражнение 2
1.
2.
- Решение простейших тригонометрических неравенств на конкретных примерах.
- Решение тригонометрических уравнений, содержащих ограничения по ОДЗ.
- Знать алгоритм решения простейших тригонометрических неравенств.
- Знать вид тригонометрических уравнений, содержащих ограничения по ОДЗ.
- Уметь решать простейшие тригонометрические неравенства.
- Уметь решать тригонометрические уравнения с ограничениями по ОДЗ.
Решить уравнение:
1.
2.
3.
В предыдущих параграфах мы рассматривали различные типы тригонометрических уравнений. Все они, в конечном итоге, сводятся к решению простейших тригонометрических уравнений. Есть еще один тип тригонометрических уравнений, в которых есть ограничения по ОДЗ. Напомним, что областью допустимых значений выражения называются такие значения переменных, при которых выражение имеет смысл.
Но для начала познакомимся с тригонометрическими неравнествами.
Простейшие тригонометрические неравенства
Неравенство, в котором неизвестная переменная находится под знаком синуса, косинуса, тангенса или котангенса, называется тригонометрическим неравенством.
К простейшим тригонометрическим неравенствам относятся неравенства вида (вместо знака может быть любой из ). Здесь является неизвестным,
Пример 1
Решить неравенство
 Рис. 1. Графическая интерпретация неравенства 1
Рис. 1. Графическая интерпретация неравенства 1
Решение
Косинус угла — абсцисса точки единичной окружности, полученной при повороте точки (1; 0) на угол . У двух точек В и С единичной окружности абсциссы равны (Рис. 1). Для того, чтобы получить точку В, нужно повернуть А(1; 0) на углы точку С — на углы У всех точек дуги единичной окружности, лежащей правее прямой ВС, абсциссы больше, чем . Тогда решением исходного неравенства является дуга СВ, значит,
Ответ:
Пример 2
Решить неравенство
 Рис. 2. Графическая интерпретация неравенства 2
Рис. 2. Графическая интерпретация неравенства 2
Решение
Пусть Решим неравенство Решением этого неравенства будут все точки дуги ВС (Рис. 2), т. е. Вернемся к исходной переменной:
Отсюда и
Ответ:
Пример 3
Решить неравенство
 Рис. 3. Графическая интерпретация неравенства 3
Рис. 3. Графическая интерпретация неравенства 3
Решение
По определению синус угла — это ордината точки, полученной при повороте точки А(1; 0) на этот угол. Две точки окружности В и С имеют ординаты, равные (Рис. 3). Точка В получена поворотом точки А на угол или на углы Точка С — на углы Решением исходного неравенства являются все точки окружности, лежащие ниже прямой ВС, т. к. они все имеют ординаты, меньшие . Тогда решение неравенства — интервалы
Ответ:
Пример 4
Решить неравенство
Решение
К левой части неравенства применим формулы косинуса двойного угла и следствие из основного тригонометрического тождества, перенесем слагаемое из правой части неравенства в левую:
Пусть тогда неравенство примет вид:
откуда или
Вернемся к исходной переменной:
или Первое неравенство решений не имеет, т. к. решение второго —
Ответ:
Упражнение 1
Решить неравенство:
1.
2.
3.
Пример 5
Решить уравнение
 Рис. 4. Область допустимых значений выражения из примера 5
Рис. 4. Область допустимых значений выражения из примера 5
Решение
Левая часть уравнения — дробное выражение, а дробь имеет смысл тогда,
когда знаменатель отличен от нуля. Тогда ОДЗ: , ,
«Выколем» эти точки на числовой окружности (Рис. 4).
Приравняем к нулю числитель левой части: , , откуда или Видим, что второе множество решений не удовлетворяет ОДЗ уравнения, тогда решением является
Ответ:
Пример 6
Решить уравнение
Решение
По определению котангенс угла — отношение косинуса угла к его синусу, тогда левая часть равенства имеет смысл в каждой точке окружности, кроме тех, в которых т. е. ОДЗ:
Раскроем скобки в левой части уравнения, применив определение котангенса, следствие из основного тригонометрического тождества, перенесем слагаемое из правой части в левую:
Пусть тогда уравнение примет вид: откуда Вернемся к исходной переменной: Решением первого уравнения является второго — С учетом ОДЗ уравнения решение —
Ответ:
Упражнение 2
Решить уравнение:
1.
2.
Контрольные вопросы
- Опишите алгоритм решения простейшего тригонометрического неравенства.
- При каких значениях переменной имеет смысл дробное выражение? Арифметический квадратный корень? Логарифмическое выражение?
Упражнение 1
1.
2.
3.
Упражнение 2
1.
2.

