- Вывод формул косинуса суммы и косинуса разности аргументов, примеры использования.
- Вывод формул синуса суммы и синуса разности аргументов, примеры использования.
- Вывод формул тангенса суммы и тангенса разности аргументов, примеры использования.
- Знать формулы сложения и разности аргументов.
- Уметь выводить формулы сложения и разности аргументов, применять их при вычислениях, преобразованиях тригонометрических выражений.
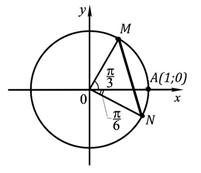 Рис. 1
Рис. 1
1. Вычислите:
1)
2)
3)
2. Упростите выражения:
1)
2)
3. Найдите расстояние между точками M и N единичной окружности, если М получена поворотом точки А(1; 0) на угол , N — на угол (рис. 1).
Из школьного курса геометрии мы знаем, что расстояние между двумя точками и можно найти по формуле
Пусть на единичной окружности есть точки А(1; 0), М1, полученная поворотом точки А на угол М2 — на угол М3 — на угол (рис. 2). Тогда каждая из этих точек будет иметь координаты:
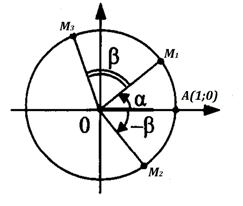 Рис. 2
Рис. 2
Треугольники М3ОА и М1ОМ2 равнобедренные, т. к. как радиусы окружности, кроме того Значит, по двум сторонам и углу между ними. Треугольники равны, соответствующие элементы равны, тогда их основания и равны.
Если равны расстояния, то и квадраты расстояний тоже равны.
Получили
Применим формулы квадрата суммы, косинуса и синуса отрицательного аргумента
Используя основное тригонометрическое тождество, получим
Вычтем из обеих частей 2 и разделим обе части равенства на –2:
(1)
Заменим в формуле (1) на
(2)
Пример 1
Вычислите
Решение
Запишем аргумент в виде суммы и применим формулу (1)
.
Ответ:
Пример 2
Вычислите
Решение
Воспользуемся формулой (2)
Ответ:
Используя формулу (2) можно доказать, что
(3)
А если в (3) вместо взять , то
(4)
Теперь выведем формулы для синуса суммы и синуса разности аргументов, т. е. для и Для вывода воспользуемся формулами (1)–(4).
т. е.
(5)
Заменим в (5) на , тем самым получим формулу для синуса разности.
,
(6)
Пример 3
Вычислите:
1)
2)
Решение
1) Представим в виде суммы и и применим формулу (5).
2) Заметим, что выражение похоже на правую часть формулы (6), тогда
Ответ: 1)
2)
Найдем чему будет равен тангенс суммы и тангенс разности аргументов.
.
Числитель и знаменатель полученной дроби разделим почленно на
Значит,
(7)
Аналогично можно доказать
(8)
Формулы (7) и (8) имеют место при , , ,
Пример 4
Упростите выражение
Решение
Воспользуемся определениями тангенса и котангенса угла и преобразуем выражение:
Ответ:
Упражнение 1
Вычислите:
1)
2)
3)
Упражнение 2
Доказать тождество
Контрольные вопросы
1. Дано тождество Какое из утверждений верно?
2. Дано тождество Какое из утверждений верно?
3. Верна ли формула Если верна, указать при каких значениях переменной.
Упражнение 1
1) ; 2) 3)
Упражнение 2
Указание.
Использовать формулы косинуса разности аргументов, синуса суммы аргументов, табличными значениями синуса и косинуса.
- Вывод формул косинуса суммы и косинуса разности аргументов, примеры использования.
- Вывод формул синуса суммы и синуса разности аргументов, примеры использования.
- Вывод формул тангенса суммы и тангенса разности аргументов, примеры использования.
- Знать формулы сложения и разности аргументов.
- Уметь выводить формулы сложения и разности аргументов, применять их при вычислениях, преобразованиях тригонометрических выражений.
 Рис. 1
Рис. 1
1. Вычислите:
1)
2)
3)
2. Упростите выражения:
1)
2)
3. Найдите расстояние между точками M и N единичной окружности, если М получена поворотом точки А(1; 0) на угол , N — на угол (рис. 1).
Из школьного курса геометрии мы знаем, что расстояние между двумя точками и можно найти по формуле
Пусть на единичной окружности есть точки А(1; 0), М1, полученная поворотом точки А на угол М2 — на угол М3 — на угол (рис. 2). Тогда каждая из этих точек будет иметь координаты:
 Рис. 2
Рис. 2
Треугольники М3ОА и М1ОМ2 равнобедренные, т. к. как радиусы окружности, кроме того Значит, по двум сторонам и углу между ними. Треугольники равны, соответствующие элементы равны, тогда их основания и равны.
Если равны расстояния, то и квадраты расстояний тоже равны.
Получили
Применим формулы квадрата суммы, косинуса и синуса отрицательного аргумента
Используя основное тригонометрическое тождество, получим
Вычтем из обеих частей 2 и разделим обе части равенства на –2:
(1)
Заменим в формуле (1) на
(2)
Пример 1
Вычислите
Решение
Запишем аргумент в виде суммы и применим формулу (1)
.
Ответ:
Пример 2
Вычислите
Решение
Воспользуемся формулой (2)
Ответ:
Используя формулу (2) можно доказать, что
(3)
А если в (3) вместо взять , то
(4)
Теперь выведем формулы для синуса суммы и синуса разности аргументов, т. е. для и Для вывода воспользуемся формулами (1)–(4).
т. е.
(5)
Заменим в (5) на , тем самым получим формулу для синуса разности.
,
(6)
Пример 3
Вычислите:
1)
2)
Решение
1) Представим в виде суммы и и применим формулу (5).
2) Заметим, что выражение похоже на правую часть формулы (6), тогда
Ответ: 1)
2)
Найдем чему будет равен тангенс суммы и тангенс разности аргументов.
.
Числитель и знаменатель полученной дроби разделим почленно на
Значит,
(7)
Аналогично можно доказать
(8)
Формулы (7) и (8) имеют место при , , ,
Пример 4
Упростите выражение
Решение
Воспользуемся определениями тангенса и котангенса угла и преобразуем выражение:
Ответ:
Упражнение 1
Вычислите:
1)
2)
3)
Упражнение 2
Доказать тождество
Контрольные вопросы
1. Дано тождество Какое из утверждений верно?
2. Дано тождество Какое из утверждений верно?
3. Верна ли формула Если верна, указать при каких значениях переменной.
Упражнение 1
1) ; 2) 3)
Упражнение 2
Указание.
Использовать формулы косинуса разности аргументов, синуса суммы аргументов, табличными значениями синуса и косинуса.



