- Арксинус числа.
- Формула решения простейшего тригонометрического уравнения
- Вычисление значений тригонометрических выражений.
- Частные случаи решения уравнения .
- Решение уравнений.
- Знать определение арксинуса числа.
- Знать формулу решения уравнения .
- Знать частные случаи решения уравнения .
- Уметь решать простейшие тригонометрические уравнения типа .
- Уметь вычислять значения тригонометрических выражений.
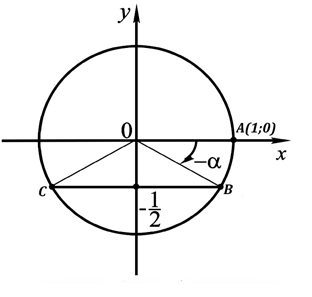 Рис. 1 Поворот точки А(1; 0) на некоторый угол
Рис. 1 Поворот точки А(1; 0) на некоторый угол
На единичной окружности отмечена точка В, ордината которой равна (Рис. 1).
Найти:
- Абсциссу точки В.
- Меру угла АОВ в радианах.
- Координаты точки С.
- Меры любых трех углов, на которые повернули точку А(1; 0), чтобы получить точки В и С (в радианах).
- Все углы, на которые нужно повернуть точку А, чтобы получить точки В и С.
Решение простейшего тригонометрического уравнения
Рассмотрим следующий вид простейших тригонометрических уравнений, а именно .
По определению, синус угла — это ордината точки единичной окружности, полученной поворотом точки (1; 0) вокруг начала координат на некоторый угол . Из определения следует, что Если т. е. когда мы выйдем за пределы единичной окружности, то уравнение корней иметь не будет. Например, уравнение .
Пример 1
Решить уравнение
Решение
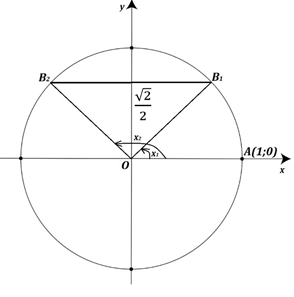 Рис. 2. Решение уравнения 1
Рис. 2. Решение уравнения 1
У точек и ординаты равны (Рис. 2). Помним, что Тогда, для того, чтобы получить точку нужно повернуть точку А(1; 0) на угол Но в нее же можно попасть и при повороте на угол Точка получается из А(1; 0) поворотом на , и на углы То есть корни уравнения можно найти по формулам , . А их, в свою очередь, можно объединить в одну: Видим, что если в этой формуле n — четное число , то получим а если n — нечетное число , получим
Ответ:
Пример 2
Решить уравнение
Решение
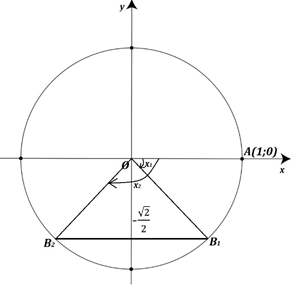 Рис. 3. Решение уравнения 2
Рис. 3. Решение уравнения 2
У точек и ординаты равны (Рис. 3). Значит,
а
т. е.
Тогда все решения уравнения можно задать одной формулой В этой формуле если n — четное число (), то получим а если n — нечетное число (), получим
Ответ:
Из решений примеров 1 и 2 видно, что уравнения и имеют бесконечное множество корней. Но, заметим, что на у каждого уравнения только один корень. Для первого уравнения это число называют арксинусом числа (обозначают ); для второго — , называют арксинусом числа () (обозначают
Вообще говоря, уравнение при (или, другими словами, при ) имеет единственный корень на отрезке , причем, если то корень лежит на отрезке , если , то на промежутке и этот корень называется арксинусом числа
Арксинусом числа a, где называется такое число синус которого равен :
, если и .
Для любого справедливо равенство
. (1)
Равенство
(2)
верно только при хотя выражение имеет смысл при всех
Для любого верно равенство
. (3)
Все корни уравнения , где , можно находить по формуле
. (4)
Пример 3
Вычислить:
а)
б)
в)
Решение
а) Так как , то — число из промежутка , синус которого равен Значит, Подставим найденные значения в исходное выражение:
б) Воспользоваться формулой (2) мы здесь не можем, т. к. . Поэтому нужно найти число из синус которого будет равен Так как где то
в) Пусть отсюда по определению арксинуса числа Тогда с новыми обозначениями нужно найти , где По следствию из основного тригонометрического тождества, с учетом того, что лежит в I или IV четверти, в которых косинус угла положительный
Ответ: а)
б)
в)
Упражнение 1
Вычислить:
1.
2.
3.
Частные случаи решения уравнения
Применим формулу (4) к простейшему тригонометрическому уравнению , когда .
(5)
(6)
(7)
Формулы (5)–(7) называют частными случаями решения уравнения .
Пример 4
Решить уравнение:
а)
б)
в)
Решение
а) Разделим обе части уравнения на 5: откуда по формуле (4) найдем корни
б) По формуле (5) имеем откуда Выразим
в) Применив формулу синуса разности, получим: откуда по (6) ,
Ответ: а)
б)
в)
Упражнение 2
Решить уравнение:
1.
2.
3. .
Контрольные вопросы
1. С помощью единичной окружности решить уравнение
2. Покажите на единичной окружности точки, соответствующие корням уравнения
3. Найдите решения уравнения на промежутке
Упражнение 1
1.
2.
3.
Упражнение 2
1.
2.
3.
- Арксинус числа.
- Формула решения простейшего тригонометрического уравнения
- Вычисление значений тригонометрических выражений.
- Частные случаи решения уравнения .
- Решение уравнений.
- Знать определение арксинуса числа.
- Знать формулу решения уравнения .
- Знать частные случаи решения уравнения .
- Уметь решать простейшие тригонометрические уравнения типа .
- Уметь вычислять значения тригонометрических выражений.
 Рис. 1 Поворот точки А(1; 0) на некоторый угол
Рис. 1 Поворот точки А(1; 0) на некоторый угол
На единичной окружности отмечена точка В, ордината которой равна (Рис. 1).
Найти:
- Абсциссу точки В.
- Меру угла АОВ в радианах.
- Координаты точки С.
- Меры любых трех углов, на которые повернули точку А(1; 0), чтобы получить точки В и С (в радианах).
- Все углы, на которые нужно повернуть точку А, чтобы получить точки В и С.
Решение простейшего тригонометрического уравнения
Рассмотрим следующий вид простейших тригонометрических уравнений, а именно .
По определению, синус угла — это ордината точки единичной окружности, полученной поворотом точки (1; 0) вокруг начала координат на некоторый угол . Из определения следует, что Если т. е. когда мы выйдем за пределы единичной окружности, то уравнение корней иметь не будет. Например, уравнение .
Пример 1
Решить уравнение
Решение
 Рис. 2. Решение уравнения 1
Рис. 2. Решение уравнения 1
У точек и ординаты равны (Рис. 2). Помним, что Тогда, для того, чтобы получить точку нужно повернуть точку А(1; 0) на угол Но в нее же можно попасть и при повороте на угол Точка получается из А(1; 0) поворотом на , и на углы То есть корни уравнения можно найти по формулам , . А их, в свою очередь, можно объединить в одну: Видим, что если в этой формуле n — четное число , то получим а если n — нечетное число , получим
Ответ:
Пример 2
Решить уравнение
Решение
 Рис. 3. Решение уравнения 2
Рис. 3. Решение уравнения 2
У точек и ординаты равны (Рис. 3). Значит,
а
т. е.
Тогда все решения уравнения можно задать одной формулой В этой формуле если n — четное число (), то получим а если n — нечетное число (), получим
Ответ:
Из решений примеров 1 и 2 видно, что уравнения и имеют бесконечное множество корней. Но, заметим, что на у каждого уравнения только один корень. Для первого уравнения это число называют арксинусом числа (обозначают ); для второго — , называют арксинусом числа () (обозначают
Вообще говоря, уравнение при (или, другими словами, при ) имеет единственный корень на отрезке , причем, если то корень лежит на отрезке , если , то на промежутке и этот корень называется арксинусом числа
Арксинусом числа a, где называется такое число синус которого равен :
, если и .
Для любого справедливо равенство
. (1)
Равенство
(2)
верно только при хотя выражение имеет смысл при всех
Для любого верно равенство
. (3)
Все корни уравнения , где , можно находить по формуле
. (4)
Пример 3
Вычислить:
а)
б)
в)
Решение
а) Так как , то — число из промежутка , синус которого равен Значит, Подставим найденные значения в исходное выражение:
б) Воспользоваться формулой (2) мы здесь не можем, т. к. . Поэтому нужно найти число из синус которого будет равен Так как где то
в) Пусть отсюда по определению арксинуса числа Тогда с новыми обозначениями нужно найти , где По следствию из основного тригонометрического тождества, с учетом того, что лежит в I или IV четверти, в которых косинус угла положительный
Ответ: а)
б)
в)
Упражнение 1
Вычислить:
1.
2.
3.
Частные случаи решения уравнения
Применим формулу (4) к простейшему тригонометрическому уравнению , когда .
(5)
(6)
(7)
Формулы (5)–(7) называют частными случаями решения уравнения .
Пример 4
Решить уравнение:
а)
б)
в)
Решение
а) Разделим обе части уравнения на 5: откуда по формуле (4) найдем корни
б) По формуле (5) имеем откуда Выразим
в) Применив формулу синуса разности, получим: откуда по (6) ,
Ответ: а)
б)
в)
Упражнение 2
Решить уравнение:
1.
2.
3. .
Контрольные вопросы
1. С помощью единичной окружности решить уравнение
2. Покажите на единичной окружности точки, соответствующие корням уравнения
3. Найдите решения уравнения на промежутке
Упражнение 1
1.
2.
3.
Упражнение 2
1.
2.
3.



