- Вывод формул приведения
- Правило для запоминания формул приведения
- Решение заданий
- Знать формулы приведения, правила записи формул приведения
- Уметь их использовать при решении задач
По рис. 1 – рис. 4 ответьте на вопросы:
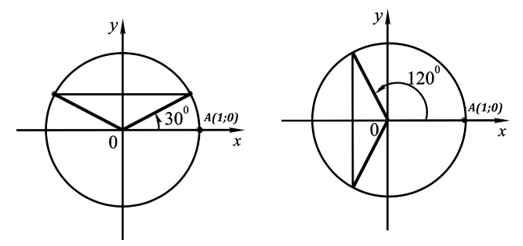 Рис. 1 Рис. 2
Рис. 1 Рис. 2
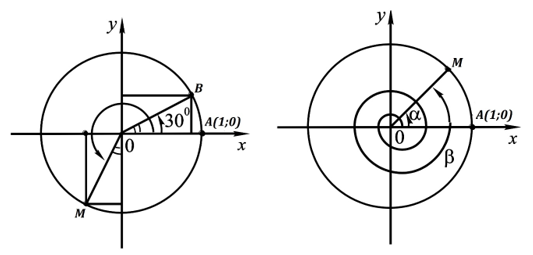 Рис. 3 Рис. 4
Рис. 3 Рис. 4
1. Синусы каких углов равны синусу (рис. 1)?
2. Косинусы каких углов равны косинусу (рис. 2)?
3. Сравните значения синуса и косинуса для точек В и М. На какой угол повернули точку А(1; 0), чтобы получить точку М (рис. 3)? На какой угол повернули точку В, чтобы получить точку М?
4. Выразите угол через (рис. 4). Сравните синусы и косинусы углов
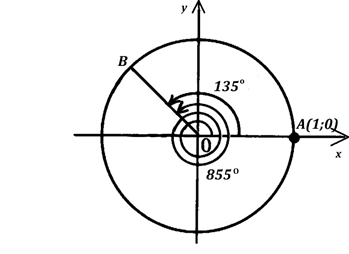 Рис. 5
Рис. 5
Вычислим значение и Как мы уже делали раньше, представим угол в виде т. е. выделим полные обороты окружности.
Значит, если повернуть точку А(1; 0) на угол , то попадем в ту же точку, что и при повороте на назовем ее точкой В (рис. 5), т. е.
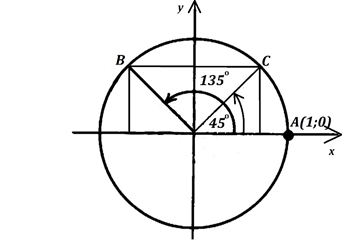 Рис. 6
Рис. 6
Построим точку С, симметричную В относительно оси ординат (рис. 6). Видно, что ординаты точек В и С одинаковые, а абсциссы отличаются знаками. Раз точка В получена из точки А поворотом на то точку С можно получить, повернув А на угол .
Поэтому
Из решения этой задачи можно заметить:
- При повороте точки А(1; 0) на угол получается та же точка, что и при повороте на угол , значит верны
(1)
(2)
- тогда
(3)
(4)
Формулы (3) и (4) можно доказать, используя уже известные нам формулы синуса разности аргументов и косинуса разности аргументов. Вообще говоря, (3) и (4) называются формулами приведения. Но только этими двумя список формул приведения не ограничивается.
Формулы приведения для синуса и косинуса угла
Все формулы справедливы для любого значения аргумента.
Пример 1
Вычислите:
1) 2)
Решение
1)
2)
Ответ: 1)
2)
Чтобы вывести формулы приведения для тангенса и котангенса угла, можно использовать определение тангенса и котангенса, например, и т. д. Приведем формулы приведения для тангенса и котангенса угла без доказательства.
Все формулы справедливы для любого допустимого значения аргумента.
Все приведенные выше формулы приведения помнить необязательно, к ним можно прийти, опираясь на правило:
Если в левой части угол равен то наименование функции остается тем же. Если угол равен то наименование функции меняется на наименование кофункции:
синус — на косинус, косинус — на синус, тангенс — на котангенс, котангенс — на тангенс. В правой части формулы ставится тот знак, который имеет левая часть при условии
Пример 2
Вычислите:
1) 2)
Решение
1) Представим аргумент в виде Тогда
Аргумент тангенса имеет вид значит, по правилу, описанному выше, наименование функции останется тем же. Угол находится в I четверти, в которой Тогда
2)
Аргумент косинуса имеет вид тогда косинус меняется на синус, угол расположен в III четверти, в которой cos<0. Получили, что
Ответ: 1)
2)
Пример 3
Определите знак числового выражения
Решение
Определим знак каждого выражения в В.
Таким образом, числитель — положительное число, знаменатель — отрицательное. Тогда выражение принимает отрицательное значение.
Ответ: отрицательное.
Пример 4
Докажите тождество
Доказательство
Рассмотрим левую часть тождества и сделаем так, чтобы аргумент функции начинался с или , для этого вынесем минус там, где это необходимо:
Применим формулы синуса и косинуса отрицательных углов тогда
Воспользуемся правилом для формул приведения: Помня, что и сократив дробь на cosx, получим а это и есть правая часть тождества.
Упражнение 1
Вычислите:
1)
2)
Упражнение 2
Докажите тождество
Контрольные вопросы
1. Замените данное выражение соответствующим обозначением тригонометрической функции: , , , .
2. Замените данное выражение соответствующим обозначением тригонометрической функции: , , , .
Упражнение 1
1) ; 2)
Упражнение 2
Указание. Используйте формулы приведения, определение котангенса угла.
- Вывод формул приведения
- Правило для запоминания формул приведения
- Решение заданий
- Знать формулы приведения, правила записи формул приведения
- Уметь их использовать при решении задач
По рис. 1 – рис. 4 ответьте на вопросы:
 Рис. 1 Рис. 2
Рис. 1 Рис. 2
 Рис. 3 Рис. 4
Рис. 3 Рис. 4
1. Синусы каких углов равны синусу (рис. 1)?
2. Косинусы каких углов равны косинусу (рис. 2)?
3. Сравните значения синуса и косинуса для точек В и М. На какой угол повернули точку А(1; 0), чтобы получить точку М (рис. 3)? На какой угол повернули точку В, чтобы получить точку М?
4. Выразите угол через (рис. 4). Сравните синусы и косинусы углов
 Рис. 5
Рис. 5
Вычислим значение и Как мы уже делали раньше, представим угол в виде т. е. выделим полные обороты окружности.
Значит, если повернуть точку А(1; 0) на угол , то попадем в ту же точку, что и при повороте на назовем ее точкой В (рис. 5), т. е.
 Рис. 6
Рис. 6
Построим точку С, симметричную В относительно оси ординат (рис. 6). Видно, что ординаты точек В и С одинаковые, а абсциссы отличаются знаками. Раз точка В получена из точки А поворотом на то точку С можно получить, повернув А на угол .
Поэтому
Из решения этой задачи можно заметить:
- При повороте точки А(1; 0) на угол получается та же точка, что и при повороте на угол , значит верны
(1)
(2)
- тогда
(3)
(4)
Формулы (3) и (4) можно доказать, используя уже известные нам формулы синуса разности аргументов и косинуса разности аргументов. Вообще говоря, (3) и (4) называются формулами приведения. Но только этими двумя список формул приведения не ограничивается.
Формулы приведения для синуса и косинуса угла
Все формулы справедливы для любого значения аргумента.
Пример 1
Вычислите:
1) 2)
Решение
1)
2)
Ответ: 1)
2)
Чтобы вывести формулы приведения для тангенса и котангенса угла, можно использовать определение тангенса и котангенса, например, и т. д. Приведем формулы приведения для тангенса и котангенса угла без доказательства.
Все формулы справедливы для любого допустимого значения аргумента.
Все приведенные выше формулы приведения помнить необязательно, к ним можно прийти, опираясь на правило:
Если в левой части угол равен то наименование функции остается тем же. Если угол равен то наименование функции меняется на наименование кофункции:
синус — на косинус, косинус — на синус, тангенс — на котангенс, котангенс — на тангенс. В правой части формулы ставится тот знак, который имеет левая часть при условии
Пример 2
Вычислите:
1) 2)
Решение
1) Представим аргумент в виде Тогда
Аргумент тангенса имеет вид значит, по правилу, описанному выше, наименование функции останется тем же. Угол находится в I четверти, в которой Тогда
2)
Аргумент косинуса имеет вид тогда косинус меняется на синус, угол расположен в III четверти, в которой cos<0. Получили, что
Ответ: 1)
2)
Пример 3
Определите знак числового выражения
Решение
Определим знак каждого выражения в В.
Таким образом, числитель — положительное число, знаменатель — отрицательное. Тогда выражение принимает отрицательное значение.
Ответ: отрицательное.
Пример 4
Докажите тождество
Доказательство
Рассмотрим левую часть тождества и сделаем так, чтобы аргумент функции начинался с или , для этого вынесем минус там, где это необходимо:
Применим формулы синуса и косинуса отрицательных углов тогда
Воспользуемся правилом для формул приведения: Помня, что и сократив дробь на cosx, получим а это и есть правая часть тождества.
Упражнение 1
Вычислите:
1)
2)
Упражнение 2
Докажите тождество
Контрольные вопросы
1. Замените данное выражение соответствующим обозначением тригонометрической функции: , , , .
2. Замените данное выражение соответствующим обозначением тригонометрической функции: , , , .
Упражнение 1
1) ; 2)
Упражнение 2
Указание. Используйте формулы приведения, определение котангенса угла.



