Конспект урока: Теорема Пифагора. Прямая теорема Пифагора. Обратная теорема Пифагора

Обратная теорема Пифагора

Не менее важной, чем теорема Пифагора, является обратная теорема. Эту теорему можно рассматривать как признак прямоугольного треугольника.

Доказательство

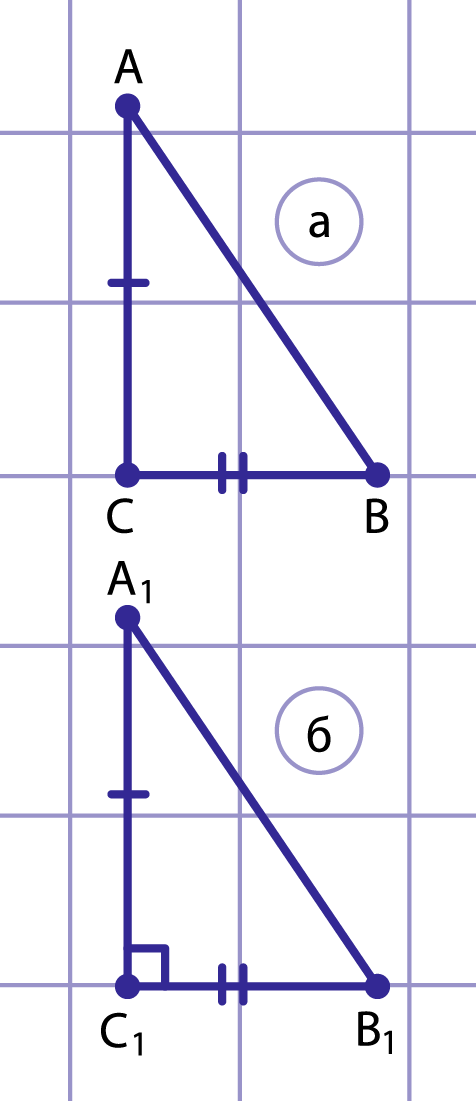Рис. 1. К доказательству теоремы

Пусть в треугольнике $ABC$ (рис. 1, а) $A{C}^2+B{C}^2=A{B}^2$.

 

Докажем, что угол $C$ прямой.

 

Рассмотрим прямоугольный треугольник $A_1{B}_1{C}_1$ с прямым углом $C_1$, в котором $A_1{C}_1=AC$, $B_1{C}_1=BC$ 
(рис. 1, б). По теореме Пифагора

 

$A_1{B_1}^2=A_1{C_1}^2+B_1{C_1}^2$, 

 

а с учетом равенства двух пар сторон рассматриваемых треугольников 

 

$A_1{B_1}^2=A{C}^2+B{C}^2=A{B}^2$, 

 

т. е. $A_1{B}_1=AB$. Тогда $△A_1{B}_1{C}_1=△ABC$ по трем сторонам, откуда $\angle C=\angle C_1=90°$.

 

Теорема доказана.

Из доказанной теоремы, в частности, следует, что треугольник со сторонами $3$, $4$ и $5$ — прямоугольный: $3^2+4^2=5^2$. Об этом знали еще древние египтяне: для построения прямых углов на местности они делили бечевку на $12$ равных частей, связывали ее концы, а потом с помощью кольев натягивали ее так, чтобы получился прямоугольный треугольник. Именно поэтому прямоугольные треугольники со сторонами, пропорциональными числам $3$, $4$ и $5$, называют египетскими треугольниками. Вообще, тройки чисел $a$, $b$, $c$, для которых выполняется равенство $a^2+b^2=c^2$, принято называть пифагоровыми тройками, а треугольники, длины сторон которых являются пифагоровыми тройками, — пифагоровыми треугольниками. 

Решение

а) Обозначим стороны треугольника $6x$, $8x$, $10x$. 

${\left(10x\right)}^2={\left(6x\right)}^2+{\left(8x\right)}^2$,

$100x^2=36x^2+64x^2$.

Следовательно, по теореме, обратной теореме Пифагора, данный треугольник прямоугольный.

б) Обозначим стороны треугольника $5x$, $6x$, $7x$.

${\left(7x\right)}^2\ne {\left(5x\right)}^2+{\left(6x\right)}^2$,

$49x^2\ne 25x^2+36x^2$.

Треугольник не является прямоугольным.

Ответ: а) является;      б) не является.

Пользуясь теоремой, обратной теореме Пифагора, составим пифагоровы тройки:

Решение

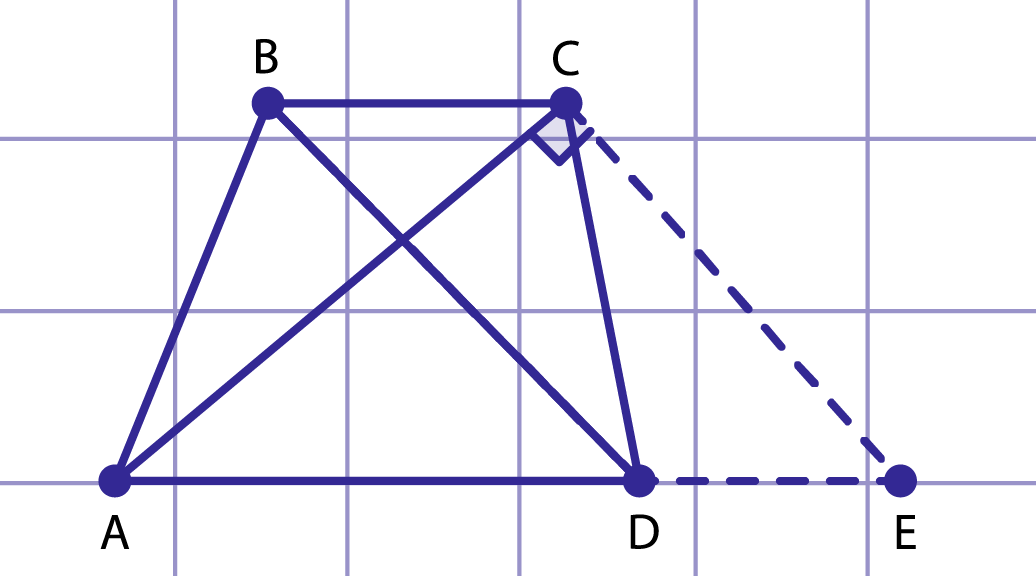Рис. 2. К решению примера 2

Рассмотрим трапецию $ABCD$ с диагоналями $AC=30 см$ и $BD=40 см$ (рис. 2). Проведем прямую $CE$ параллельную $BD$. Четырехугольник $BCED$ — параллелограмм по определению, $BC=DE$, $BD=CE$.

 

Тогда в треугольнике  $ACE$ $AC=30 см$, $CE=40 см$, $AE=8 см+42 см=50 см$. По теореме, обратной теореме Пифагора, треугольник $ACE$  прямоугольный, $AC\perp CE$. Высота трапеции $ABCD$ и треугольника $ACE$ равны, обозначим $h$.

 

$S_{ABCD}=\frac{1}{2}(AD+BC)·h$

 

$S_{△ACE}=\frac{1}{2}AE·h=\frac{1}{2}(AD+BC)·h$.

 

Площадь треугольника $ACE$ равна площади трапеции $ABCD$, площадь прямоугольного треугольника равна половине произведения катетов.

 

$S_{ABCD}=\frac{1}{2}AC·CE=\frac{1}{2}AC·BD=\frac{1}{2}·30·40=600 \left(с{м}^2\right)$.

 

Ответ: $600 с{м}^2$.

Для вычисления площади трапеции $ABCD$ можно воспользоваться теоремой о площади четырехугольника со взаимно перпендикулярными диагоналями.

Упражнение 1

1. а) нет;       б) да;        в) нет;         г) нет.

2. $45°$.

Упражнение 2

1. Медиана $12,5 см$, высота $12 см$.

2. По теореме обратной теореме Пифагора диагонали параллелограмма взаимно перпендикулярны, значит данный параллелограмм — ромб.