Цифровая библиотека

Интернет-библиотека по школьным предметам от «Онлайн-школы». Библиотека поможет решить домашнее задание, подготовиться к контрольной и вспомнить прошлые темы.

Например: формулы сокращенного умножения

Выбери класс

Выбери все классы

Все предметы
8 класс
Геометрия
Четыре замечательные точки треугольника

Геометрия 8 класс Геометрия 8 класс

Конспект урока: Четыре замечательные точки треугольника

Треугольники

18.01.2025

3247

Четыре замечательные точки треугольника. Свойства биссектрисы угла. Свойства серединного перпендикуляра к отрезку. Теорема о пересечении высот треугольника

План урока

Доказать теорему о биссектрисе угла и следствия из нее;
Определить понятие серединного перпендикуляра к отрезку;
Доказать свойство серединного перпендикуляра к отрезку и следствия из него;
Доказать теорему о пересечении высот треугольника;
Рассмотреть применение свойств замечательных точек треугольника для решения задач.

Цели урока

Знать определение серединного перпендикуляра к отрезку, теоремы о биссектрисе угла треугольника, серединном перпендикуляре к отрезку и следствия из них, теорему о пересечении высот треугольника;
Уметь применять теоремы и следствия из них при решении задач.

Разминка

Сформулируйте свойство медиан треугольника.
Один из углов треугольника равен 60°. Под каким углом пересекаются биссектрисы двух других его углов.
Один из углов треугольника равен 60°. Под каким углом пересекаются высоты, проведенные к сторонам этого угла.

Свойства биссектрисы угла

Теорема

Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон.

Обратно: каждая точка, лежащая внутри угла и равноудаленная от сторон угла, лежит на его биссектрисе.

Доказательство

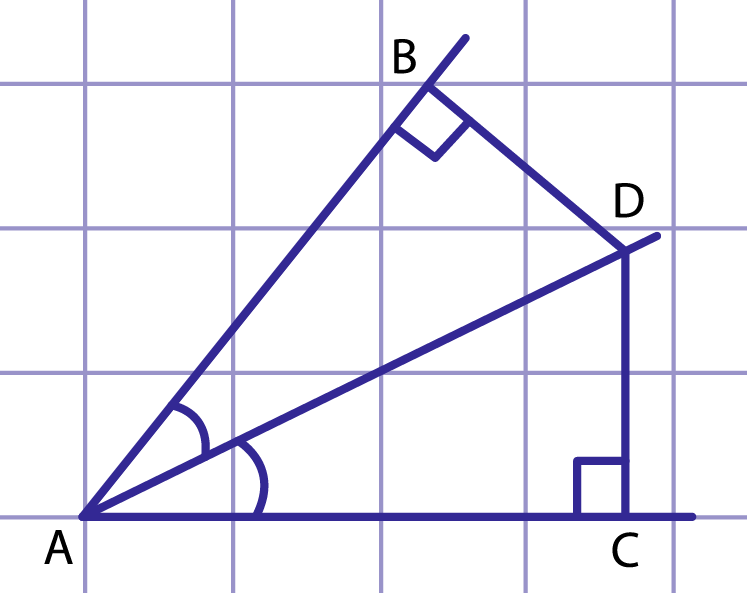Рис. 1. Точка биссектрисы угла равноудалена от его сторон

Пусть даны неразвернутый угол с вершиной $A$ и точка $D$ на его биссектрисе (рис. 1). Проведем из точки $D$ перпендикуляры $D B$ и $D C$ к сторонам данного угла. По определению $D B$ и $D C$ — расстояния от точки $D$ до сторон угла $A$ .

Прямоугольные треугольники $D B A$ и $D C A$ имеют общую гипотенузу $D A$ , $∠ D A B = ∠ D A C$ по условию. Тогда $∆ D B A = ∆ D C A$ по гипотенузе и острому углу. Отсюда $D B = D C$ , то есть точка $D$ равноудалена от сторон данного угла.

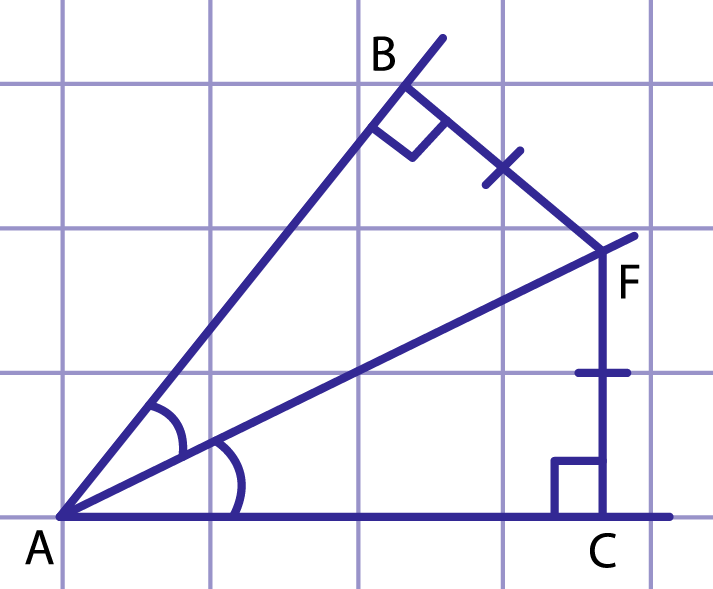Рис. 2. Точка, равноудаленная от сторон угла, принадлежит его биссектрисе

Теперь докажем, что любая точка, равноудаленная от сторон угла, принадлежит его биссектрисе. Пусть $F$ — некоторая точка, равноудаленная от сторон угла $A$ , то есть перпендикуляры $F B$ и $F C$ , проведенные из точки $F$ к сторонам данного угла, равны (рис. 2). Соединим точки $F$ и $A$ . Тогда прямоугольные треугольники $F B A$ и $F C A$ равны по гипотенузе и катету. Отсюда $∠ F A B = ∠ F A C$ , то есть луч $A F$ — биссектриса угла $A$ .

Теорема доказана.

Следствие 1

Геометрическим местом точек плоскости, лежащих внутри неразвёрнутого угла и равноудаленных от сторон угла, является биссектриса этого угла.

Следствие 2

Биссектрисы углов треугольника пересекаются в одной точке.

Доказательство следствия 2

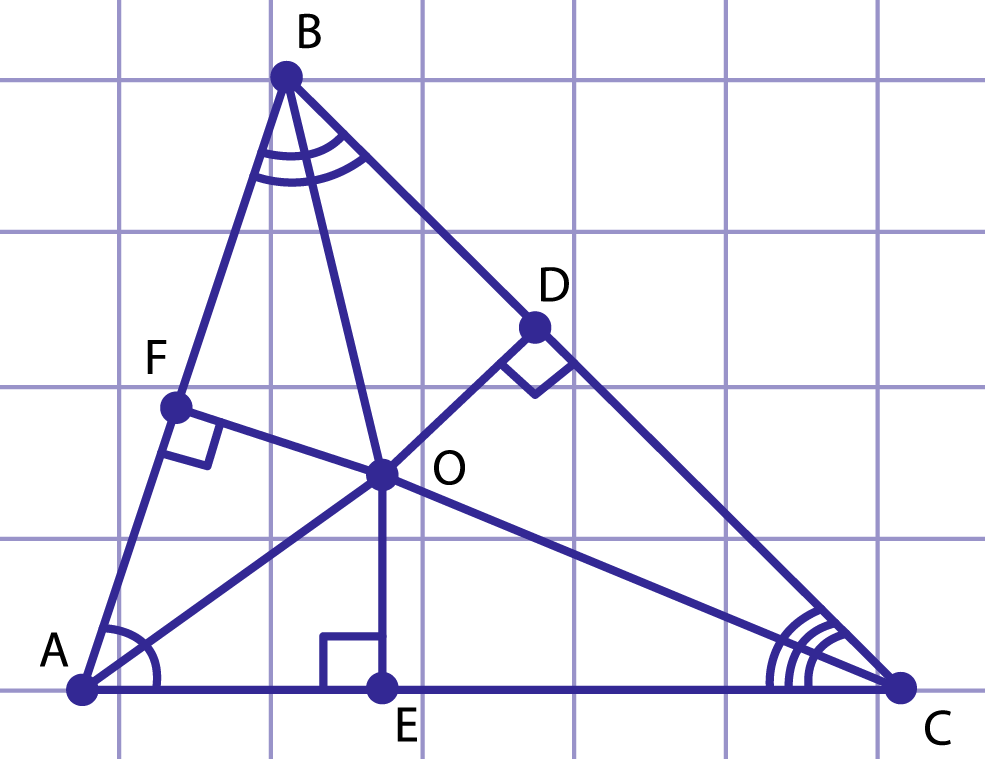Рис. 3. Биссектрисы треугольника ABC пересекаются в одной точке

Рассмотрим треугольник $A B C$ , биссектрисы углов $A$ и $B$ пересекаются в точке $O$ (рис. 3). Опустим перпендикуляры $O F$ , $O D$ и $O E$ из точки $O$ к прямым $A B$ , $B C$ и $A C$ соответственно. По теореме точки биссектрисы угла равноудалены от сторон угла, поэтому $O E = O F$ , $O F = O D$ , следовательно, $O E = O D$ . Таким образом, точка $O$ равноудалена от сторон угла $С$ , следовательно, лежит на его биссектрисе, $C O$ – биссектриса угла $С$ .

Все три биссектрисы треугольника $A B C$ пересекаются в точке $O$ , что и требовалось доказать.

Пример 1

В треугольнике $A B C$ $∠ A = 80 °$ , $∠ B = 60 °$ , а их биссектрисы пересекаются в точке $H$ . Найдите угол $A C H$ .

Решение

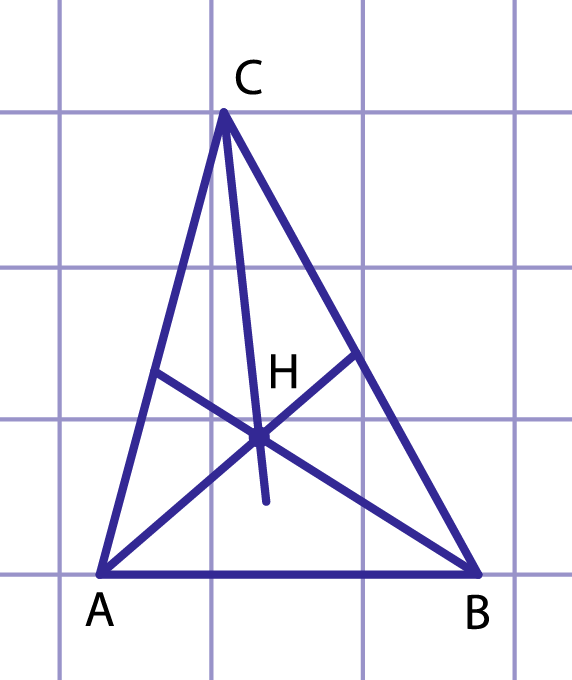Рис. 4. К решению примера 1

По следствию 2 $C H$ – биссектриса угла $С$ (рис. 4), следовательно $∠ A C H = \frac{1}{2} ∠ C$ .

$∠ C = 180 ° - (∠ A + ∠ B) = 180 ° - (80 ° + 60 °) = 40 °$ , $∠ A C H = \frac{1}{2} \cdot 40 ° = 20 °$ .

Ответ: 20°.

Свойство серединного перпендикуляра к отрезку

Серединным перпендикуляром к отрезку называется прямая, проходящая через середину данного отрезка и перпендикулярная к нему.

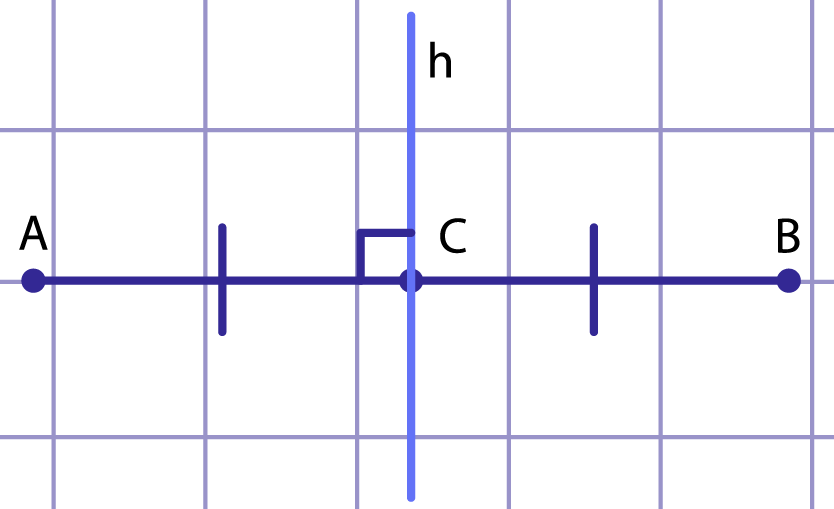Рис. 5. Серединный перпендикуляр к отрезку AB

На рисунке 5 $h$ - серединный перпендикуляр к отрезку $A B$ .

Теорема

Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.

Обратно: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.

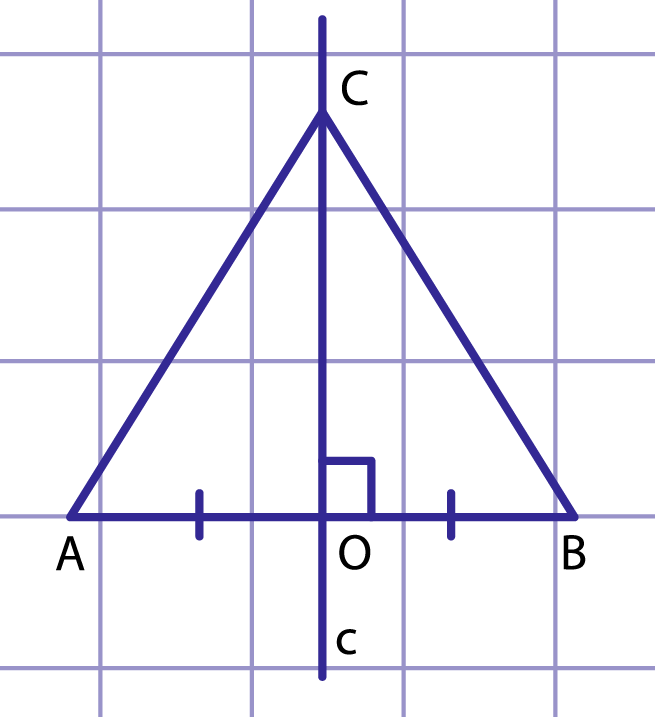Рис. 6. К доказательству первой части свойства серединного перпендикуляра к отрезку

Доказательство

Пусть произвольная точка $С$ лежит на прямой $c$ , перпендикулярной отрезку $A B$ и проходящей через его середину — точку $O$ (рис. 6). В треугольнике $A C B$ отрезок $C O$ — медиана и высота, значит, этот треугольник равнобедренный с основанием $A B$ . Отсюда $A C = B C$ , то есть расстояния от точки $С$ до концов отрезка $A B$ равны.

Случай, когда точки $С$ и $O$ совпадают, рассмотрите самостоятельно.

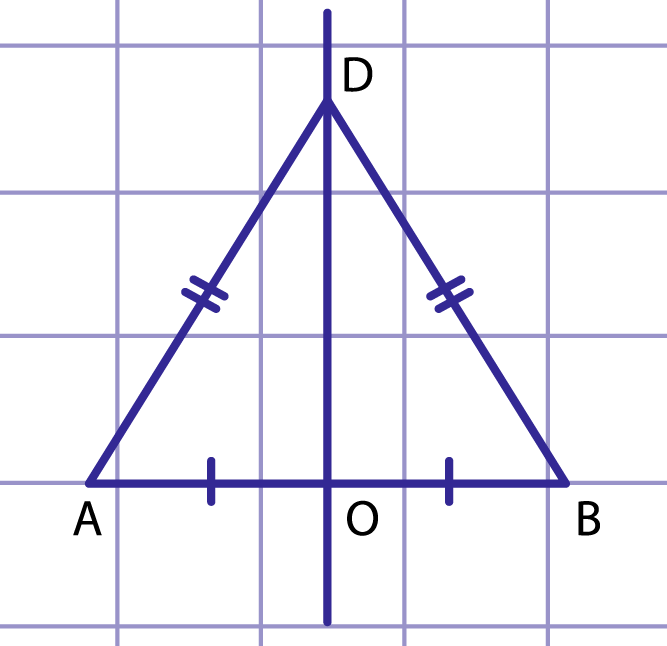Рис. 7. К доказательству второй части свойства серединного перпендикуляра к отрезку

Докажем обратное утверждение.

Пусть произвольная точка $D$ равноудалена от точек $A$ и $B$ , то есть $A D = B D$ (рис. 7). Тогда в равнобедренном треугольнике $A D B$ отрезок $D O$ — медиана, проведенная к основанию, которая является также и высотой. Таким образом, прямая $D O$ — серединный перпендикуляр к отрезку $A B$ .

Случай, когда точки $D$ и $O$ совпадают, рассмотрите самостоятельно.

Теорема доказана.

Следствие 1

Геометрическим местом точек плоскости, равноудаленных от концов отрезка, является серединный перпендикуляр к этому отрезку.

Следствие 2

Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.

Доказательство следствия 2

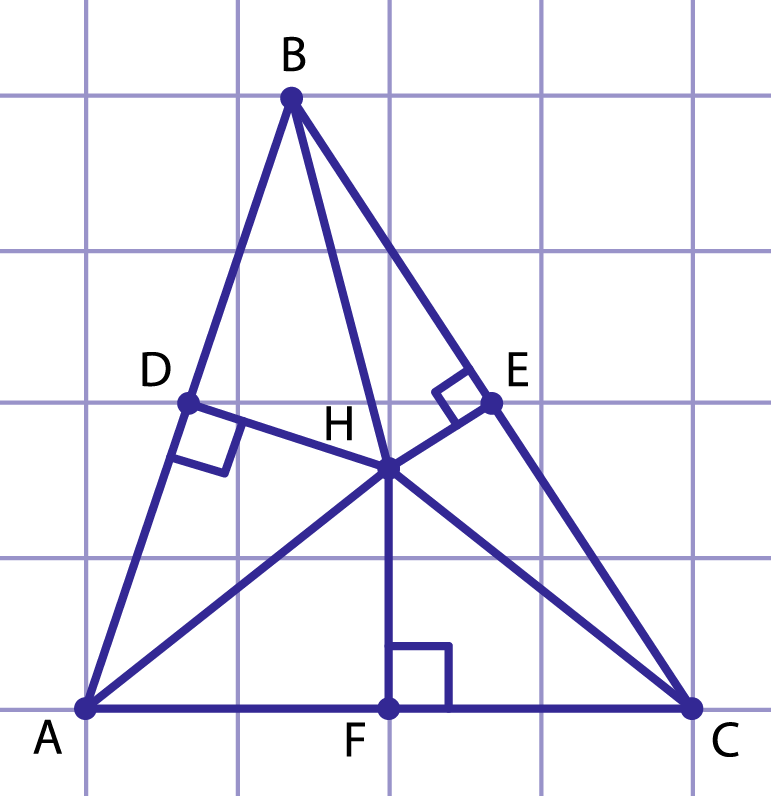Рис. 8. Серединные перпендикуляры треугольника ABC пересекаются в одной точке

Рассмотрим треугольник $A B C$ $H D$ , $H E$ – серединные перпендикуляры к сторонам $A B$ и $B C$ соответственно (рис. 8).

Перпендикуляры к сторонам угла $B$ пересекаются в одной точке, иначе они были бы параллельны. Допустим, $H D ∥ H E$ , тогда прямая $A B ⊥ H D$ и $A B ⊥ H E$ , но $B C ⊥ H E$ , значит $A B ∥ B C$ , чего не может быть.

По доказанному свойству серединного перпендикуляра $H A = H B$ , $H B = H C$ , следовательно $H A = H C$ . Тогда точка $H$ лежит на серединном перпендикуляре к отрезку $A C$ . Таким образом, все три серединных перпендикуляра к сторонам треугольника $A B C$ пересекаются в одной точке, что и требовалось доказать.

Теорема о пересечении высот треугольника

Теорема

Высоты треугольника (или их продолжения) пересекаются в одной точке.

Доказательство

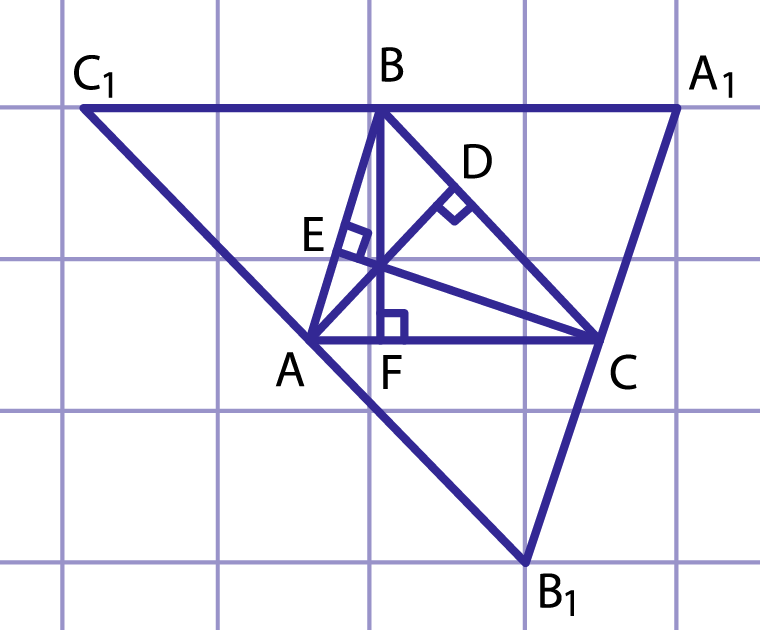Рис. 9. Высоты треугольника ABC пересекаются в одной точке

Пусть $A D$ , $B F$ и $C E$ — высоты треугольника $A B C$ (рис. 9). Проведя через вершины треугольника $A B C$ прямые, параллельные противолежащим сторонам, получим треугольник $A_{1} B_{1} C_{1}$ , стороны которого перпендикулярны высотам треугольника $A B C$ . По построению четырехугольники $C_{1} B C A$ и $B_{1} A B C$ — параллелограммы, откуда $C_{1} A = B C$ и $B C = A B_{1}$ . Следовательно, точка $A$ — середина отрезка $B_{1} C_{1}$ . Аналогично доказываем, что $B$ — середина $A_{1} C_{1}$ и
$C$ — середина $A_{1} B_{1}$ .

Таким образом, высоты $A D$ , $B F$ и $C E$ лежат на серединных перпендикулярах к сторонам треугольника $A_{1} B_{1} C_{1}$ , которые пересекаются в одной точке.

Теорема доказана.

Таким образом, замечательными точками треугольника являются:

точка пересечения биссектрис;
точка пересечения серединных перпендикуляров к сторонам;
точка пересечения медиан;
точка пересечения высот (или их продолжений).

Пример 2

Точка $H$ – точка пересечения высот треугольника $A B C$ . Докажите, что точка $A$ – точка пересечения высот треугольника $H B C$ .

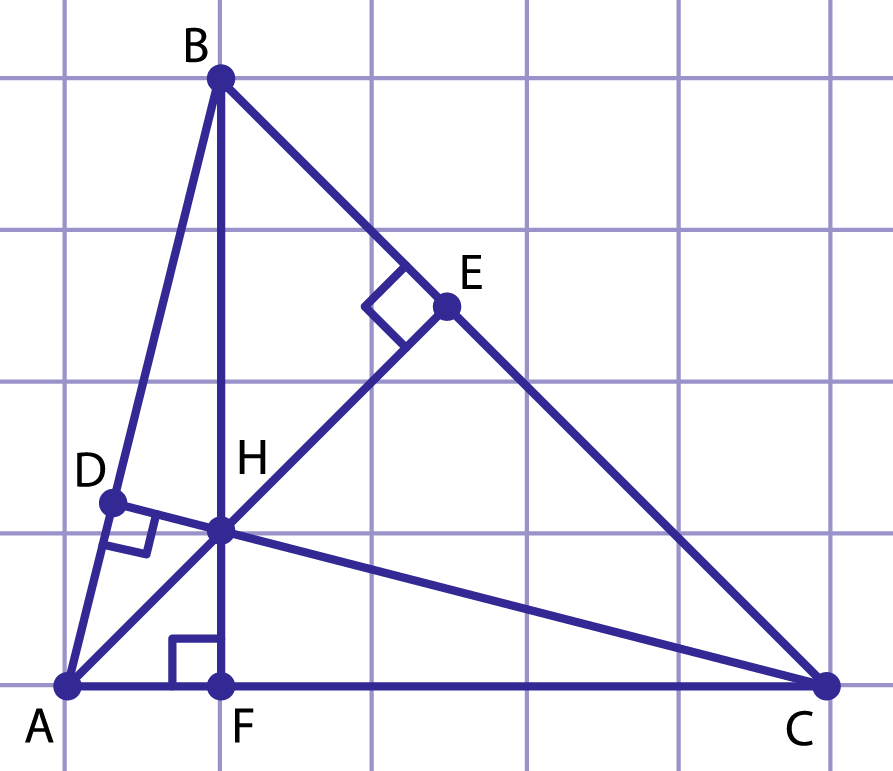Рис. 10. К примеру 2

Решение

Рассмотрим треугольник $A B C$ , высоты $A E$ , $B F$ , $C D$ пересекаются в точке $H$ (рис. 10). Докажем, что высоты треугольника $H B C$ пересекаются в точке $A$ .

Поскольку $A E ⊥ B C$ , $B F ⊥ A C$ , $C D ⊥ A B$ , то высотами треугольника $H B C$ являются отрезки $H E$ , $B D$ , $C F$ , которые пересекаются в точке $A$ , что и требовалось доказать.

Упражнения

1. Точка $K$ лежит внутри угла $B M C$ и находится на одинаковом расстоянии от сторон угла, $∠ B M K = 54 °$ . Найдите $∠ B M C$ .

2. $P K$ – серединный перпендикуляр к отрезку $N L$ , $P L = 4$ , $N L = 7$ . Найдите периметр треугольника $P N L$ .

3. Серединные перпендикуляры к сторонам треугольника $A B C$ пересекаются в точке $O$ . Найдите длину стороны $A B$ , если $O A = 8 с м,$ $∠ A O B = 60 °$ .