Конспект урока: Средняя линия треугольника

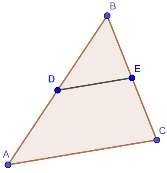Рис. 1. DE — средняя линия ∆ABC

Рассмотрим треугольник $ABC$, $DE$ — его средняя линия (рис. 1). 

По определению средней линии треугольника $DB=\frac{1}{2}AB$, $EB=\frac{1}{2}CB$, тогда треугольники $ABC$ и $DBE$ подобны по двум пропорциональным сторонам и углу между ними ($\angle B$ — общий, $\frac{AB}{DB}=\frac{CB}{EB}=2$).

Тогда $\angle BAC=\angle BDE$, а они соответственные при пересечении прямых $AC$ и $DE$  секущей $AB$, следовательно $AC\parallel DE$. 

Поскольку коэффициент подобия треугольников равен $2$, то $AC=2DE$ или $DE=\frac{1}{2}AC$. 

Теорема доказана. 

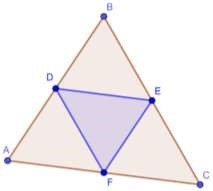Рис. 2. К решению примера 1

Рассмотрим $∆ABC$, $P_{ABC}=76$ см, $DE$, $EF$, $DF$ — средние линии треугольника, $EF : DF : DE = 4 : 7 : 8$ (рис. 2). 

Треугольники $ABC$ и $DEF$ подобны по трем пропорциональным сторонам, т. к. $DE=\frac{1}{2}AC$, $EF=\frac{1}{2}AB$, $DF=\frac{1}{2}BC$ по свойству средней линии треугольника. Следовательно отношение сторон треугольника $ABC$ такое же, как в треугольнике $DEF,$ т.е. $AB : BC : AC = 4 : 7 : 8$. 

Пусть $x$ — одна часть, тогда  $AB=4x$, $BC=7x$, $AC=8x$. Периметр треугольника равен сумме длин сторон, тогда: 

$4x+7x+8x=76$, 

$19x = 76$,

$x=4$. 

$4·4=16$ (см) — $AB$, 

$7·4 = 28$(см) — $BC$, 

$8·4 = 32$ (см) — $AC$.

Ответ: $16$ см, $28$ см, $32$ см. 

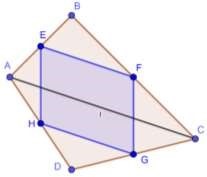Рис. 3. Теорема Вариньона

Рассмотрим четырехугольник $ABCD$, $E$, $F$, $G$, $H$ — середины сторон данного четырехугольника. Докажем, что $EFGH$ — параллелограмм (рис. 3). 

В треугольнике $ABC$: $EF$— средняя линия, значит, $EF\parallel AC$, $EF=\frac{1}{2}AC$. В треугольнике $ADC$: $GH$ — средняя линия, значит, $GH\parallel AC$, $GH=\frac{1}{2}AC$. 

Получили, что в четырехугольнике $EFGH$ противоположные стороны $EF=GH$ и $EF\parallel GH$, следовательно $EFGH$ — параллелограмм, что и требовалось доказать.

Докажите теорему Вариньона для невыпуклого четырехугольника самостоятельно. 

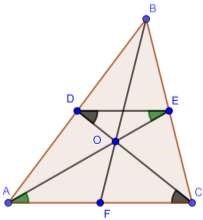Рис. 4. К доказательству свойства медиан

Рассмотрим треугольник $ABC$, $AE$, $BF$, $CD$ — медианы треугольника, медианы $AE$ и $CD$ пересекаются в точке $O$ (рис. 4). 

Так как $D$ — середина $AB$, $E$ — середина $BC$, 
то $DE$ — средняя линия треугольника $ABC$, по свойству средней линии треугольника $DE=\frac{1}{2}AC$, $DE\parallel AC$, тогда накрест лежащие углы при параллельных прямых равны: $\angle OAC=\angle OED$, $\angle OCA=\angle ODE$. 

Треугольники $AOC$ и $EOD$ подобны по двум углам, следовательно: 

$\frac{AC}{DE}=\frac{AO}{OE}=\frac{CO}{OD}=\frac{2}{1}$.

Таким образом, точка пересечения медиан $AE$ и $CD$ делит их в отношении $2 : 1$ считая от вершины. 

Аналогично доказываем, что точка пересечения медиан $BF$ и $CD$ делит каждую из них в отношении $2 : 1$, считая от вершины, значит совпадает с точкой $O$. 

Все три медианы пересекаются в одной точке и точкой пересечения делятся в отношении $2 : 1$, считая от вершины, что и требовалось доказать.