Цифровая библиотека

Интернет-библиотека по школьным предметам от «Онлайн-школы». Библиотека поможет решить домашнее задание, подготовиться к контрольной и вспомнить прошлые темы.

Например: формулы сокращенного умножения

Выбери класс

Выбери все классы

Все предметы
8 класс
Геометрия
Признаки подобия треугольников

Геометрия 8 класс Геометрия 8 класс

Конспект урока: Признаки подобия треугольников

Треугольники

17.01.2025

3802

Признаки подобия треугольников

План урока

Признаки подобия треугольников;
Примеры применения признаков подобия треугольников.

Цели урока

Знать признаки подобия треугольников;
Уметь доказывать подобие треугольников с применением признаков подобия.

Разминка

Какие треугольники называют подобными?
Какие отрезки называют пропорциональными?
Какими свойствами обладают параллельные прямые?

Первый признак подобия треугольников

Теорема (признак подобия треугольников по двум углам)

Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.

Доказательство

Рассмотрим $∆ A B C$ и $∆ A_{1} B_{1} C_{1}$ в которых $∠ A = ∠ A_{1}$ , $∠ C = ∠ C_{1}$ (рис. 1). Докажем, что $∆ A B C$ ~ $∆ A_{1} B_{1} C_{1}$ .

По теореме о сумме углов треугольника

$∠ B = 180 ° - ∠ A - ∠ C$ ,

$∠ B_{1} = 180 ° - ∠ A_{1} - ∠ C_{1}$ , следовательно $∠ B = ∠ B_{1}$ . Углы треугольника $A B C$ равны углам треугольника $A_{1} B_{1} C_{1}$ .

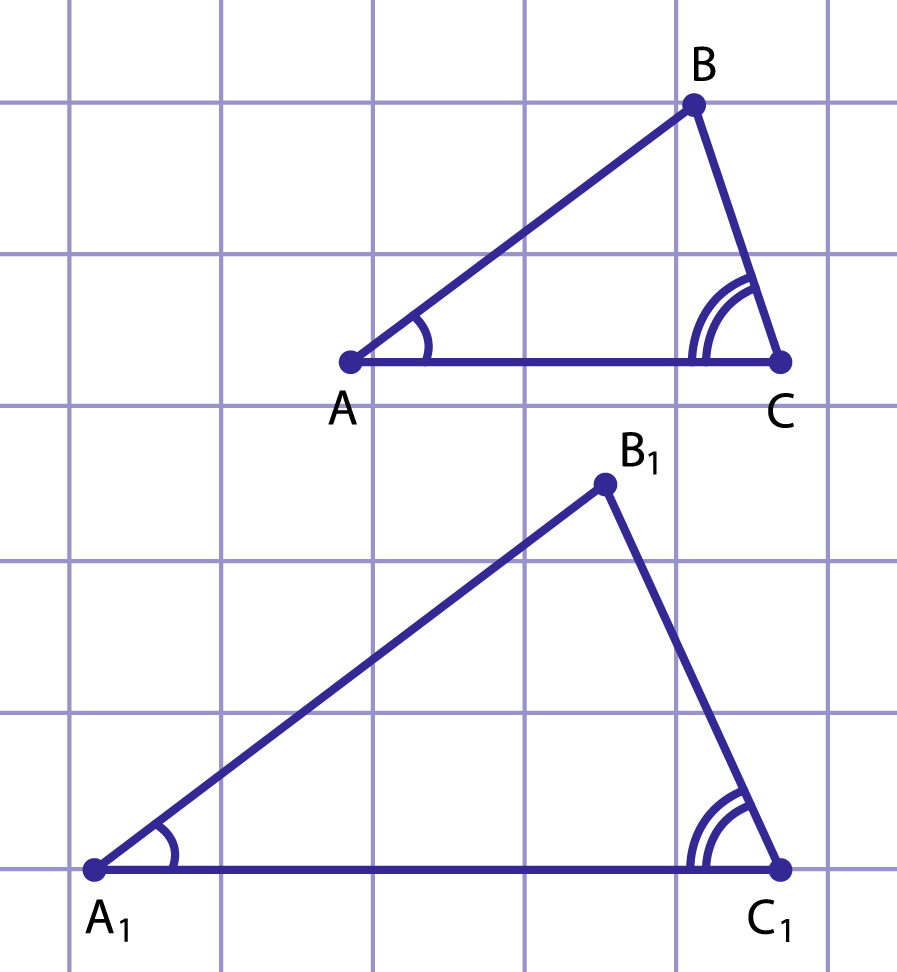Рис. 1. К доказательству первого признака подобия треугольников

Докажем пропорциональность сторон треугольников $A B C$ и $A_{1} B_{1} C_{1}$ . Поскольку треугольники имеют равные углы, воспользуемся теоремой об отношении площадей треугольников с равными углами:

$\frac{S_{A B C}}{S_{A_{1} B_{1} C_{1}}} = \frac{A B \cdot A C}{A_{1} B_{1} \cdot A_{1} C_{1}} = \frac{B C \cdot A C}{B_{1} C_{1} \cdot A_{1} C_{1}} = = \frac{A B \cdot B C}{A_{1} B_{1} \cdot B_{1} C_{1}} .$

Следовательно,

$\frac{A B}{A_{1} B_{1}} = \frac{B C}{B_{1} C_{1}} = \frac{A C}{A_{1} C_{1}}$ .

Стороны треугольника $A B C$ пропорциональны сходственным сторонам треугольника $A_{1} B_{1} C_{1}$ , следовательно $A B C$ ~ $A_{1} B_{1} C_{1}$ по определению.

Теорема доказана.

Пример 1

На сторонах $A B$ и $B C$ треугольника $A B C$ выбраны точки $M$ и $K$ соответственно так, что $M K ∥ A C$ , $M B : M A = 2 : 5$ . Найдите площадь четырехугольника $A M K C$ , если площадь треугольника $A B C$ равна 98 см².

Решение

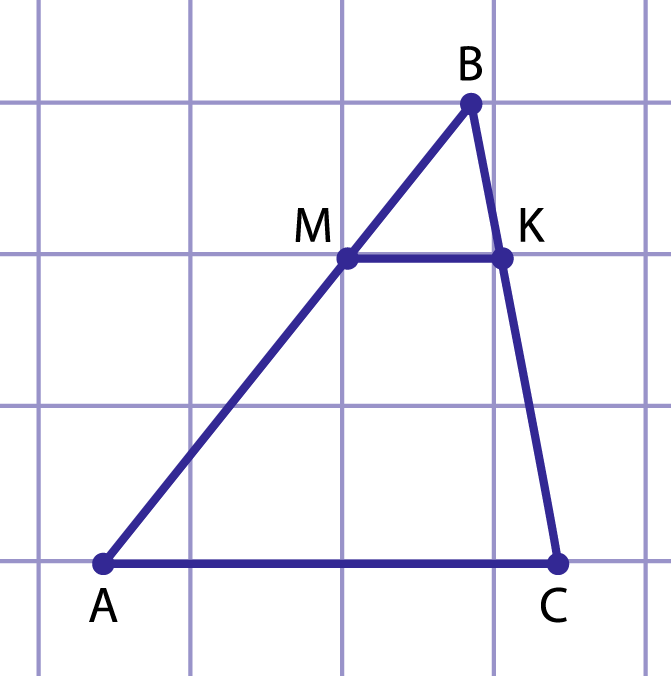Рис. 2. К решению примера 1

Рассмотрим треугольник $A B C$ , $M K ∥ A C$ (рис. 2).

В треугольниках $A B C$ и $M B K$ $∠ B A C = ∠ B M K$ , $∠ B C A = ∠ B K M$ как соответственные углы при параллельных прямых $M K$ и $A C$ и секущих $A B$ , $B C$ соответственно, следовательно $∆ A B C$ ~ $∆ M B K$ по двум углам.

В подобных треугольниках соответственные стороны пропорциональны

$\frac{A B}{M B} = \frac{B C}{B K} = \frac{A C}{M K} = k$ ,

т.к. $M B : M A = 2 : 5$ , то $k = \frac{A B}{M B} = 3, 5$ . По теореме об отношении площадей подобных треугольников

$\frac{S_{A B C}}{S_{M B K}} = k^{2} = (3, 5)^{2} = 12, 25$ .

$S_{A B C} = 98 с м^{2}$ , $S_{M B K} = 98 : 12, 25 = 8 (с м^{2})$ .

$S_{A M K C} = S_{A B C} - S_{M B K} = 98 - 8 = 90 (с м^{2})$ .

Ответ: 90 см².

Второй признак подобия треугольников

Теорема (признак подобия треугольников по двум пропорциональным сторонам и углу между ними)

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то такие треугольники подобны.

Доказательство

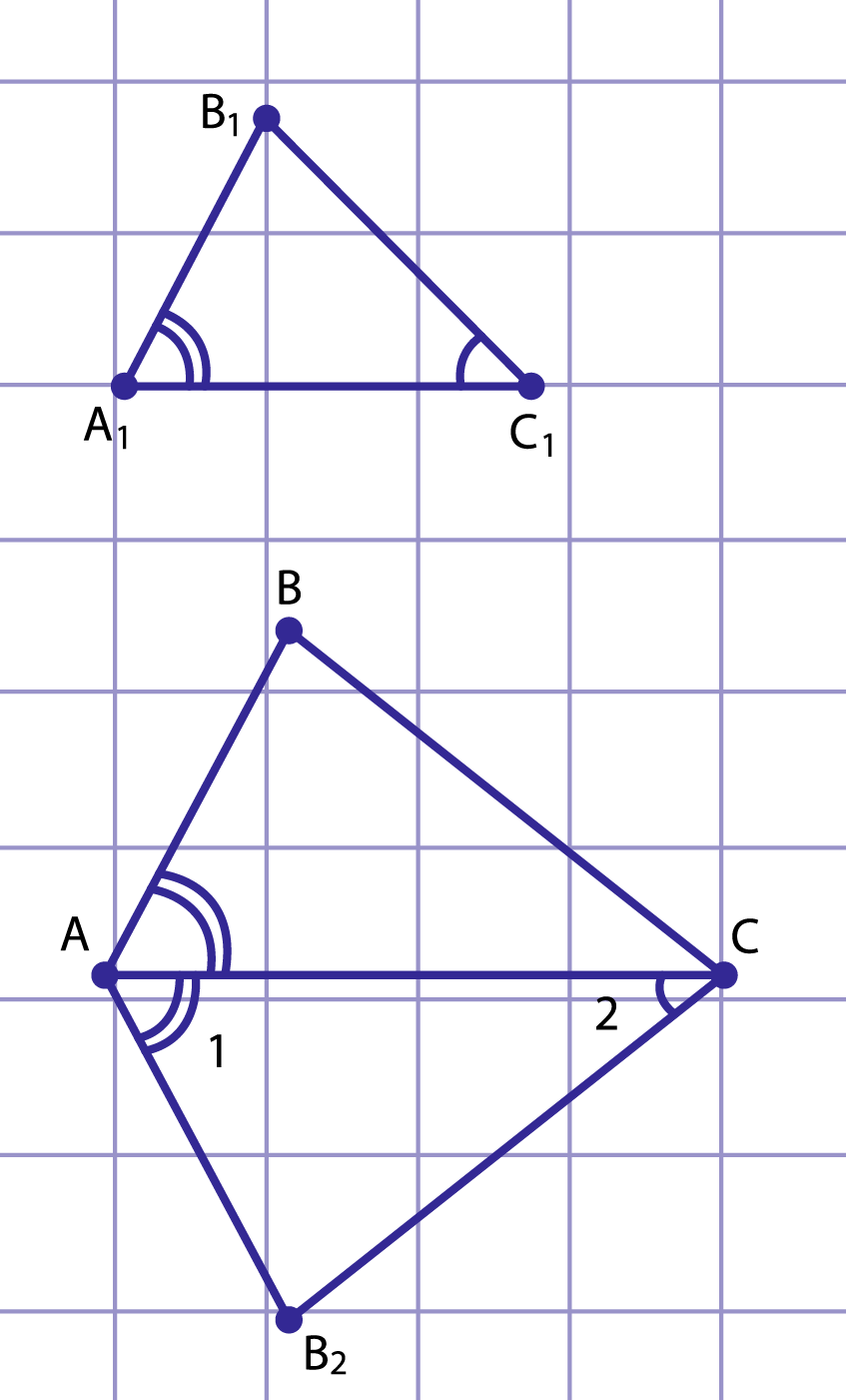Рис. 3. К доказательству второго признака

Рассмотрим $∆ A B C$ и $∆ A_{1} B_{1} C_{1}$ , $\frac{A B}{A_{1} B_{1}} = \frac{A C}{A_{1} C_{1}}$ , $∠ A = ∠ A_{1}$ (рис. 3). Докажем, что $∆ A B C$ ~ $∆ A_{1} B_{1} C_{1}$ .

Рассмотрим треугольник $A B_{2} C$ , в котором $∠ 1 = ∠ A_{1}$ , $∠ 2 = ∠ C_{1}$ (рис. 3). Треугольники $A B_{2} C$ и $A_{1} B_{1} C_{1}$ подобны по первому признаку подобия треугольников, тогда $\frac{A B_{2}}{A_{1} B_{1}} = \frac{A C}{A_{1} C_{1}}$ .

По условию $\frac{A B}{A_{1} B_{1}} = \frac{A C}{A_{1} C_{1}}$ , следовательно $A B = A B_{2}$ .

Треугольники $A B C$ и $A B_{2} C$ равны по двум сторонам и углу между ними ( $A C$ – общая сторона, $A B = A B_{2}$ , $∠ 1 = ∠ B A C$ ). Тогда $∠ A C B = ∠ 2$ и $∠ 2 = ∠ С_{1}$ , значит $∠ С = ∠ С_{1}$ . Треугольники $A B C$ и $A_{1} B_{1} C_{1}$ подобны по первому признаку.

Теорема доказана.

Пример 2

Прямая, пересекающая стороны $B A$ и $B C$ треугольника $A B C$ , делит каждую из них в отношении $m : n$ , считая от вершины $B$ . Докажите, что данная прямая параллельна стороне $A C$ .

Решение

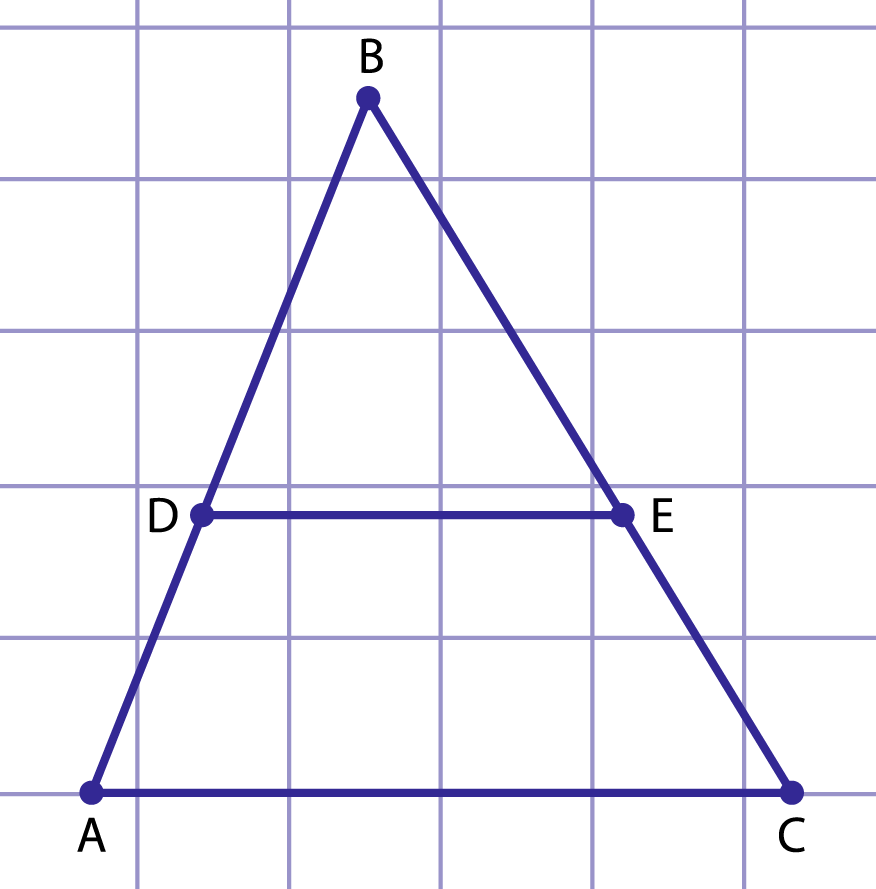Рис. 4. К решению примера 2

Пусть в треугольнике $A B C$ прямая $D E$ пересекает стороны $B A$ и $B C$ в точках $D$ и $E$ соответственно (рис. 4), причем $\frac{B D}{A D} = \frac{B E}{C E} = \frac{m}{n}$ .

Рассмотрим треугольники $A B C$ и $D B E$ , в которых $∠ B$ – общий, $\frac{A B}{B D} = \frac{B C}{B E} = \frac{m + n}{m}$ .

Следовательно $∆ A B C$ ~ $∆ D B E$ по второму признаку подобия. В подобных треугольниках соответственные углы равны, значит $∠ B A C = ∠ B D E$ , а это соответственные углы при прямых $A C$ и $D E$ и секущей $A B$ , поэтому $D E ∥ A C$ , что и требовалось доказать.

Третий признак подобия треугольников

Теорема (признак подобия треугольников по трем сторонам)

Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.

Доказательство

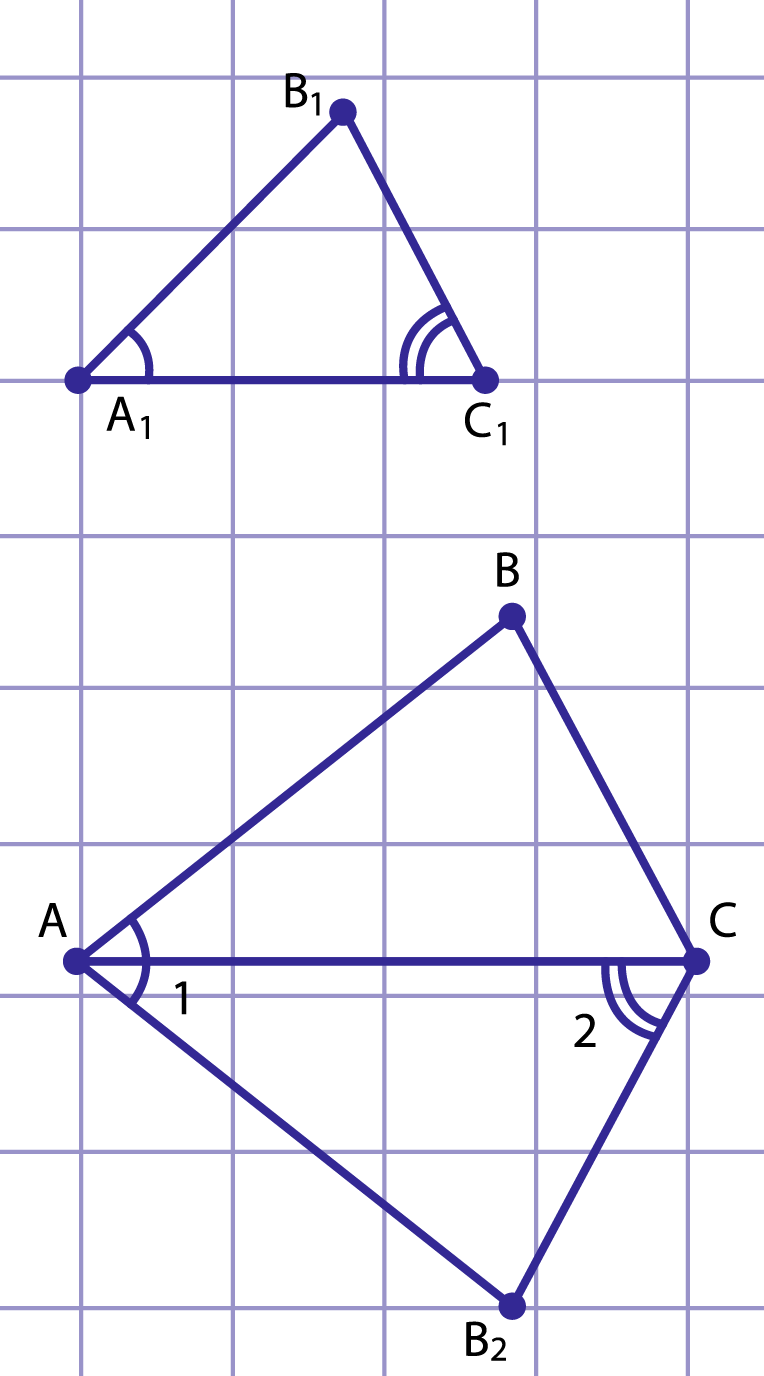Рис. 5. К доказательству третьего признака

Пусть стороны треугольников $A B C$ и $A_{1} B_{1} C_{1}$ пропорциональны:

$\frac{A B}{A_{1} B_{1}} = \frac{B C}{B_{1} C_{1}} = \frac{A C}{A_{1} C_{1}}$ .

Докажем, что $∆ A B C$ ~ $∆ A_{1} B_{1} C_{1}$ .

По второму признаку подобия для этого достаточно доказать, что $∠ A = ∠ A_{1}$ .

Рассмотрим треугольник $A B_{2} C$ , у которого $∠ 1 = ∠ A_{1},$ $∠ 2 = ∠ C_{1}$ (рис. 5). Треугольники $A B_{2} C$ и $A_{1} B_{1} C_{1}$ подобны по первому признаку подобия треугольников, поэтому

$\frac{A B_{2}}{A_{1} B_{1}} = \frac{A C}{A_{1} C_{1}} = \frac{B_{2} C}{B_{1} C_{1}}$ .

По условию $\frac{A B}{A_{1} B_{1}} = \frac{B C}{B_{1} C_{1}} = \frac{A C}{A_{1} C_{1}}$ .

Таким образом, $A B = A B_{2}$ , $B C = B_{2} C$ . Треугольники $A B C$ и $A B_{2} C$ равны по трем сторонам, следовательно $∠ 1 = ∠ B A C$ , а т.к. $∠ 1 = ∠ A_{1}$ , то $∠ B A C = ∠ A_{1}$ . Треугольники $A B C$ и $A_{1} B_{1} C_{1}$ подобны по второму признаку.

Теорема доказана.

Пример 3

Основание и боковая сторона одного равнобедренного треугольника равны 12 см и 10 см, а основание другого равнобедренного треугольника и проведенная к нему медиана равны 18 см и 12 см. Подобны ли данные треугольники?

Решение

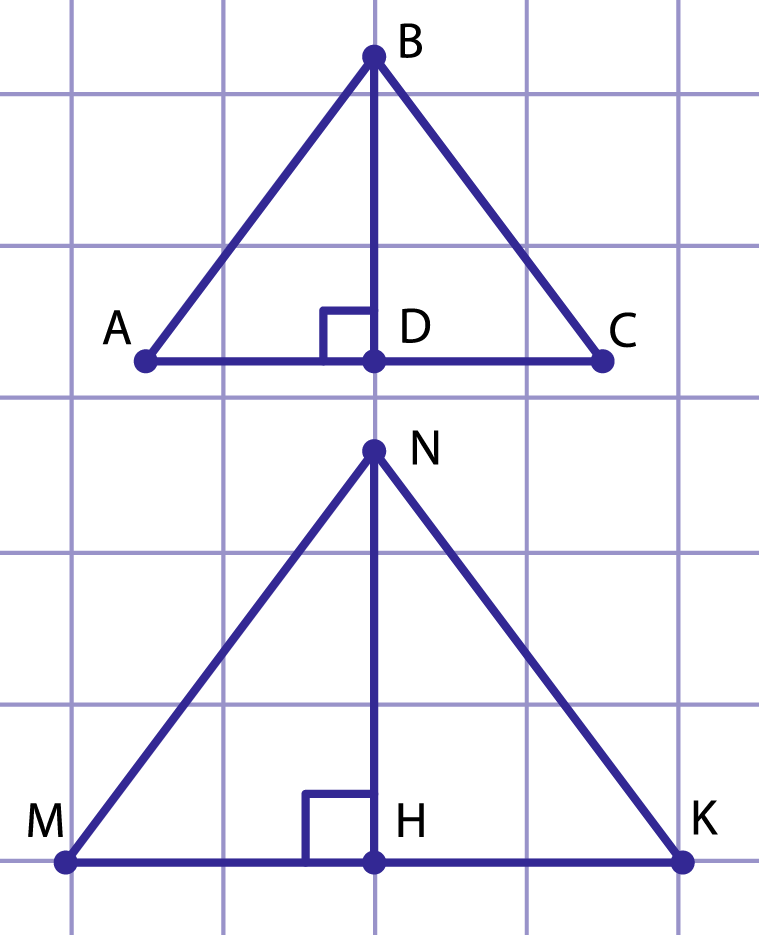Рис. 6. К решению примера 3

Рассмотрим равнобедренные треугольники $A B C$ и $M N K$ , $A B = B C = 10 с м$ , $A C = 12 с м$ , $M K = 18 с м$ , $N H$ – медиана и высота треугольника $M N K$ , проведенная к основанию, $N H = 12 с м$ (рис. 6).

В треугольнике $M N H$ $M H = 9 с м$ , $N H = 12 с м$ , $∠ H = 90 °$ по теореме Пифагора $M N^{2} = N H^{2} + M H^{2}$ , $M N = \sqrt{9^{2} + 12^{2}} = 15 (с м)$ .

Проверим пропорциональность сторон треугольников $A B C$ и $M N K$ :

$\frac{10}{15} = \frac{12}{18} = \frac{10}{15}$ .

Следовательно, $∆ A B C$ ~ $∆ M N K$ по третьему признаку.

Ответ: треугольники подобны.

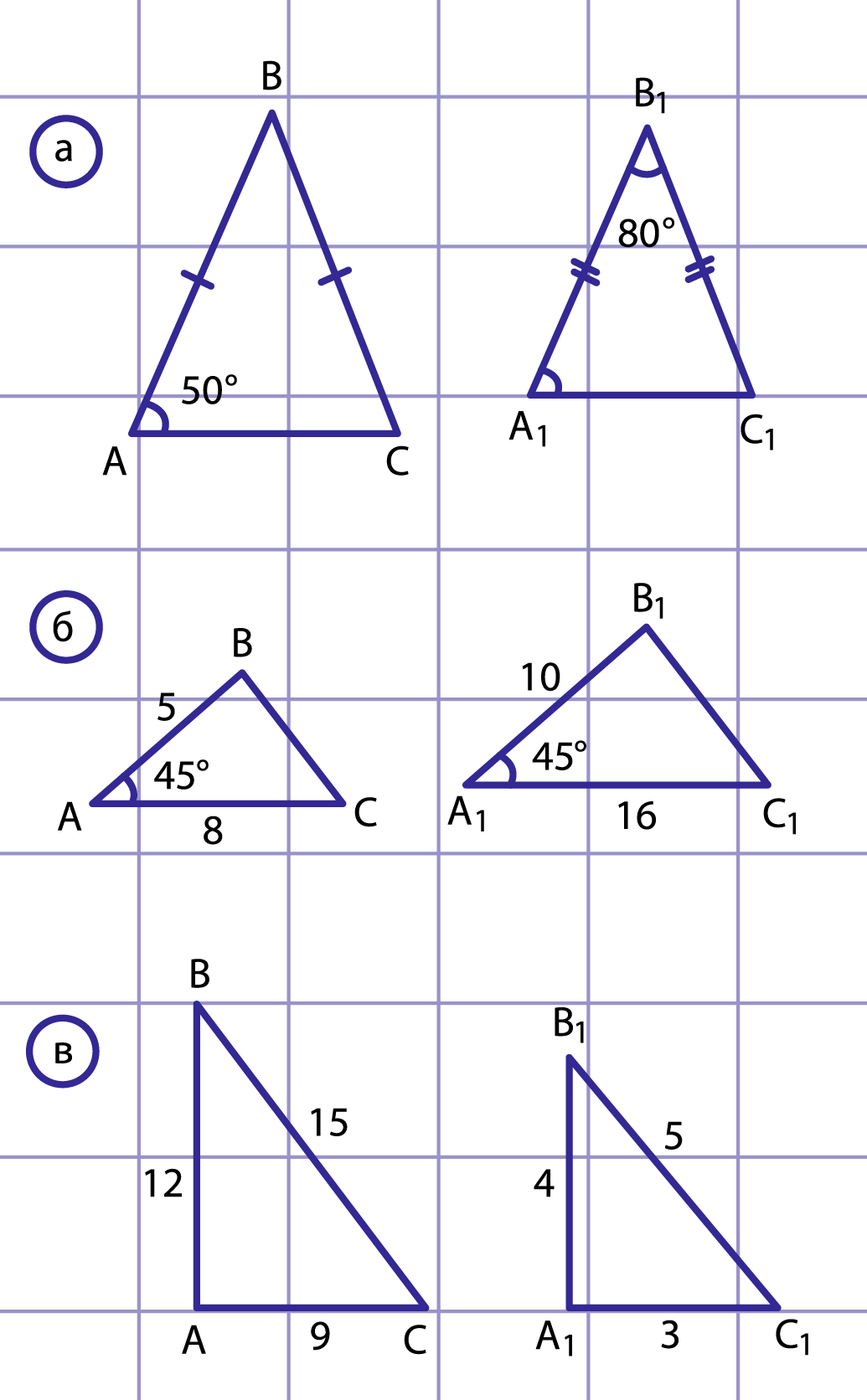Рис. 7. К задаче 1

Упражнения

1. По данным рисунка 7 докажите подобие треугольников $A B C$ и $A_{1} B_{1} C_{1}$ .

2. Продолжения боковых сторон $A B$ и $C D$ трапеции $A B C D$ пересекаются в точке $O$ . Докажите, что $∆ A O D$ ~ $∆ B O C$ . Найдите $A D$ , если $B C = 4 с м$ , $O B = 6 с м,$ $O A = 9 с м$ .

3. На одной стороне неразвернутого угла $O$ отложены отрезки $O A = 9 с м$ и $O B = 12 с м$ , а на другой стороне — отрезки $O C = 6 с м$ и $O H = 18 с м$ . Подобны ли треугольники $O A C$ и $O B H ?$ Подобны ли треугольники $O B C$ и $O H A$ ?

4. Определите, подобны ли треугольники со сторонами:

а) 3, 4, 6 и 9, 15, 18;

б) 2, 3, 3 и 8, 12, 12.

Контрольные вопросы

1. В треугольниках $A B C$ и $A_{1} B_{1} C_{1}$ $\frac{A B}{A_{1} B_{1}} = \frac{B C}{B_{1} C_{1}} = k$ . Какое равенство необходимо добавить к условию, чтобы можно было доказать подобие этих треугольников? Назовите все возможные варианты ответа.

2. Даны треугольники $A B C$ и $K M N$ , в которых $\frac{A B}{K N} = \frac{B C}{M N} = \frac{A C}{M K}$ . Назовите угол треугольника $K M N$ , равный углу $C$ . Почему эти углы равны?

3. Даны треугольники $A B C$ и $K M N$ , в которых $\frac{A B}{B C} = \frac{M N}{N K}$ и $∠ B = ∠ N$ . Назовите угол треугольника $A B C$ , равный углу $M$ . Почему эти углы равны?

4. Могут ли быть подобными:

а) прямоугольный и равнобедренный треугольники;

б) прямоугольный и равносторонний треугольники;

в) треугольник с углом 50° и треугольник с углом 100°;

г) треугольник с углом 60° и треугольник с углом 120°?

5. Подобны ли равнобедренные треугольники, если они имеют:

а) по равному острому углу;

б) по равному тупому углу?

6. Два подобных треугольника имеют общий угол. Обязательно ли их стороны, противолежащие этому углу, параллельны? Приведите контрпример.

Ответы на упражнения

1. а) подобны по первому признаку;

б) подобны по второму признаку;

в) подобны по третьему признаку.

2. Треугольники $∆ A O D$ и $∆ B O C$ подобны по первому признаку, $A D = 6 с м$ .

3. $∆ O A C$ и $∆ O B H$ не являются подобными; $∆ O B C$ ~ $∆ O H A$ по второму признаку.

4. а) нет; б) да.

Предыдущий урок

Средняя линия треугольника

Треугольники

Следующий урок

Значения синуса, косинуса и тангенса для углов 30, 45 и 60 градусов

Треугольники

Урок подготовил(а)

Валерия Александровна

Учитель математики

Опыт работы: более 20 лет

Пропорциональные отрезки в прямоугольном треугольнике

Геометрия
Измерение силы тока и напряжения. Зависимость силы тока от напряжения. Закон Ома для участка цепи. Сопротивление проводника

Физика
Внешняя политика России в 1741—1762 гг.

История

Зарегистрируйся, чтобы присоединиться к обсуждению урока

Добавьте свой отзыв об уроке, войдя на платфому или зарегистрировавшись.

Отзывы об уроке:

Пока никто не оставил отзыв об этом уроке