Франция при старом порядке

Решение неравенств второй степени с одной переменной

План урока

Неравенства второй степени с одной переменной;
Алгоритм решения неравенств.

Цели урока

Знать определение неравенства второй степени с одной переменной, алгоритм решения неравенств второй степени с одной переменной;
Уметь решать неравенства второй степени с одной переменной.

Разминка

Какие есть способы решения квадратных уравнений?
При каком условии квадратное уравнение не имеет корней?
При каком значении коэффициента $a$ ветви параболы, графика квадратичной функции $y = a x^{2} + b x + c$ , направлены вверх?

Неравенства второй степени с одной переменной

В жизни вы часто сталкиваетесь со сравнениями: ценами в разных магазинах, доходов и расходов. Неравенства так же, как и уравнения, помогают решать важные задачи математики, экономики, практической жизнедеятельности. Например, в экономике есть зависимость прибыли от объема производства, и важно понимать, при каком объеме производства прибыль будет превышать издержки. Поэтому уметь решать неравенства также необходимо.

Одними из ключевых неравенств являются неравенства второй степени с одной переменной.

Неравенства вида $a x^{2} + b x + c > 0$ и $a x^{2} + b x + c < 0$ , где $x$ - переменная, $a$ , $b$ и $c$ - некоторые числа и $a \neq 0$ называют неравенствами второй степени с одной переменной.

Алгоритм решения неравенства второй степени

Вам известно, что решение любого неравенства, в отличии от решения уравнения, в основном, есть промежуток или несколько промежутков. Тогда решить неравенство вида $a x^{2} + b x + c > 0$ или $a x^{2} + b x + c < 0$ означает найти промежутки, где выражение $a x^{2} + b x + c$ принимает положительные или отрицательные значения.

Решение неравенства второй степени очень похоже на решение квадратного уравнения. Отличие состоит в том, что после нахождения корней квадратного трёхчлена, которые разбивают область определения на промежутки, необходимо выбрать нужные промежутки. Приведем алгоритм решения неравенств второй степени с одной переменной.

Алгоритм решения неравенств вида $a x^{2} + b x + c > 0$ и $a x^{2} + b x + c < 0$

Найти дискриминант квадратного трёхчлена $a x^{2} + b x + c$ и выяснить имеет ли трёхчлен корни.
Если трёхчлен имеет корни, то отметить их на оси $x$ и через них провести схематически параболу, ветви которой направлены вверх при $a > 0$ или вниз при $a < 0$ ; если трёхчлен не имеет корней, то схематически изобразить параболу, расположенную в верхней полуплоскости при $a > 0$ или в нижней полуплоскости при $a < 0$ .
Найти на оси $x$ промежутки, для которых точки параболы расположены выше оси $x$ (если решают неравенство $a x^{2} + b x + c > 0$ ) или ниже оси $x,$ если решают неравенство $a x^{2} + b x + c < 0$ .

Пример 1

Решить неравенство $x^{2} - 3 x + 2 > 0$ .

Решение

1. Найдем корни трёхчлена $x^{2} - 3 x + 2$ , для этого решим уравнение:

$x^{2} - 3 x + 2 = 0$ ,

$D = (- 3)^{2} - 4 \cdot 1 \cdot 2 = 1$ ,

$x_{1} = \frac{3 - 1}{2} = 1$ , $x_{2} = \frac{3 + 1}{2} = 2$ .

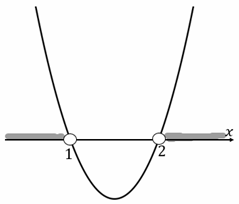Рис. 1. Решение неравенства
x²– 3x + 2 > 0

2. Квадратный трёхчлен имеет два корня. Это значит, что парабола, заданная функцией $y = x^{2} - 3 x + 2$ , пересекает ось $x$ в двух точках, причём ветви параболы направлены вверх, так как $a = 1$ .

3. Изобразим эту параболу и отметим промежутки, на которых парабола находится в верхней полуплоскости.

По рисунку 1 видно, что парабола лежит выше оси $x$ на промежутках $(- \infty; 1)$ и $(2; + \infty)$ . Значит, решением неравенства является объединение этих промежутков, т.е. $(- \infty; 1) \cup (2; + \infty)$ .

Ответ: $(- \infty; 1) \cup (2; + \infty)$ .

По рисунку 1 также можно сделать вывод, что решением неравенства $x^{2} - 3 x + 2 < 0$ , будет интервал $(1; 2)$ , т.к. на этом промежутке парабола лежит ниже оси $x$ .

Пример 2

Решить неравенство $- x^{2} + 6 x - 9 < 0$ .

Решение

1. Найдем корни трёхчлена $- x^{2} + 6 x - 9$ :

$- x^{2} + 6 x - 9 = 0$ , $x^{2} - 6 x + 9 = 0$

$D = (- 6)^{2} - 4 \cdot 1 \cdot 9 = 0$

$x = \frac{6}{2} = 3$ .

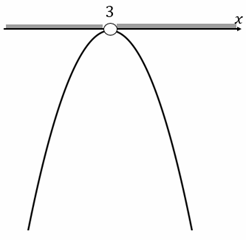Рис. 2 Решение неравенства
-x²+ 6x - 9 < 0

2. Квадратный трёхчлен имеет один корень. Это значит, что парабола, заданная функцией $y = - x^{2} + 6 x - 9$ , пересекает ось $x$ в одной точке, ее ветви направлены вниз, так как $a = - 1$ .

Изобразим эту параболу и отметим промежутки, на которых парабола находится в нижней полуплоскости.

По рисунку 2 видно, что парабола лежит ниже оси $x$ на промежутках $(- \infty; 3)$ и $(3; + \infty)$ . Значит, решением неравенства является объединение этих промежутков, т.е. $(- \infty; 3) \cup (3; + \infty)$ .

Ответ: $(- \infty; 3) \cup (3; + \infty)$ .

Обратим внимание, что неравенство $- x^{2} + 6 x - 9 > 0$ не имеет решения, так как по рисунку 2 видно, что вся парабола лежит не выше оси $x$ .

Пример 3

Решить неравенство $5 x^{2} + 3 x + 2 > 0$ .

Решение

1. Найдем корни трёхчлена $5 x^{2} + 3 x + 2$ :

$5 x^{2} + 3 x + 2 = 0$ ,

$D = (3)^{2} - 4 \cdot 5 \cdot 2 = - 31 < 0$ ,

т.е. корней нет.

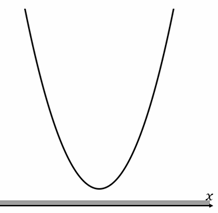Рис. 3. Решение неравенства 5x²+3x+2>0

2. Квадратный трёхчлен не имеет корней. Это значит, что парабола, заданная функцией $y = 5 x^{2} + 3 x + 2$ , не пересекает ось $x$ . Её ветви направлены вверх, так как $a = 5$ .

3. Изобразим эту параболу и отметим промежутки, на которых парабола находится в верхней полуплоскости.

По рисунку 3 видно, что вся парабола лежит выше оси $x$ . Значит, решение – множество всех действительных чисел.

Ответ: $x$ - любое число.

Заметим, что неравенство $5 x^{2} + 3 x + 2 < 0$ не имеет решения, так как по рисунку 3 видно, что вся парабола лежит выше оси $x$ .

Упражнение

Решить неравенство:

$2 x^{2} + 5 x - 3 \geq 0$
$- x^{2} - 5 x - 6 > 0$
$9 x^{2} - 6 x + 1 \leq 0$
$2 x^{2} - 5 x + 7 < 0$

Контрольные вопросы:

1. Как решить неравенство второй степени с одной переменной?

2. Может ли неравенство второй степени с одной переменной не иметь решения?

3. Чем отличается решение неравенства $x^{2} - 3 x + 2 \geq 0$ от решения неравенства $x^{2} - 3 x + 2 > 0$ из примера 1?

Ответы

Упражнение

1. $(- \infty; - 3] \cup [\frac{1}{2}; + \infty)$ . 2. $(- 3; - 2)$ . 3. $x = \frac{1}{3}$ . 4. нет решений

Конспект урока: Квадратные неравенства

Решение уравнений и неравенств

Неравенства второй степени с одной переменной