Конспект урока: Уравнение с двумя переменными и его график

Уравнение с двумя переменными

Мы уже много раз говорили о необходимости уметь решать уравнения, и вы уже умеете решать некоторые виды уравнений с одной переменной. Но в задачах довольно часто встречаются уравнения с несколькими переменными. Рассмотрим уравнения с двумя переменными.

Очевидно, что новый вид уравнения отличается от старых в первую очередь тем, что теперь оно будет содержать сразу две переменные. Каждое из следующих уравнений является тем самым уравнением с двумя переменными

$4x+5y=14$, $x^2+5=y$, $y^2+2x^2-x=1$.

Решить уравнение с одной переменной $x$ означало, что необходимо найти такое значение $x$, при котором уравнение обращалось в верное равенство. Значит, можно сделать вывод, что для того, чтобы решить уравнение с двумя переменными $x$ и $y$, необходимо найти значения для $x$ и $y$, при которых уравнение обращается в верное равенство. Это второе отличие.

Для уравнения с двумя переменными $x$ и $y$ решение записывается в виде пары чисел $(x_0; y_0)$, где $x_0, y_0$ - решение этого уравнения.

Например, для уравнения $4x+5y=14$ пара чисел $(1; 2)$ является решением уравнения, так как при подстановке $4·1+5·2=14$, $14=14$, получаем верное равенство.

Уравнение с двумя переменными, как правило, имеет бесконечное множество решений.

Для того, чтобы определить степень уравнения с двумя переменными, необходимо привести его к виду, где левая часть есть многочлен стандартного вида, а правая часть – нуль. Тогда степень уравнения будет совпадать со степенью этого многочлена.

Определить степень уравнения с двумя переменными 

$(3x-2y^2{)}^2=9x^2-1$.

Решение

Преобразуем уравнение. Для этого раскроем скобки, перенесем слагаемые из правой части в левую и приведем подобные слагаемые:

$9x^2-12x{y}^2+4y^4-9x^2+1=0$,

$4y^4-12x{y}^2+1=0$.

В левой части получили многочлен $4y^4-12x{y}^2+1$, степень которого равна 4. Значит, степень уравнения $(3x-2y^2{)}^2=9x^2-1$ тоже равна 4.

Ответ: 4.

1. Определить какие пары чисел являются решениями уравнения $y^2+2x^2-x=1$

а) (1; 0)  б) (-1; 1)   в) (0; 1)    г) (0: -1)   д) (2; 2)

2. Определить степень уравнения $(x^2+y^3{)}^2=(y^2-1{)}^3$

График уравнения с двумя переменными

Мы уже выяснили, что решением уравнения с двумя переменными является пара чисел и, как правило, таких решений бесконечно много. Эти решения можно изобразить на координатной плоскости.

Графики некоторых уравнений вы уже умеете строить. Например, график линейного уравнения $ax+by=c$, где $a\ne 0$и $b\ne 0$, — это прямая, а график уравнения $y=a{x}^2+bx+c$ — парабола.

Но вообще графики уравнений с двумя переменными могут принимать абсолютно любой вид. На рисунке 1 вы можете увидеть некоторые из них.

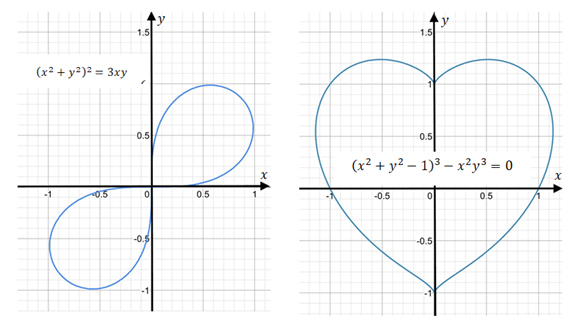Рис. 1. Графики функций (x²+y² )²=3xy и (x²+y²-1)³-x² y³=0

Уравнение окружности и ее график

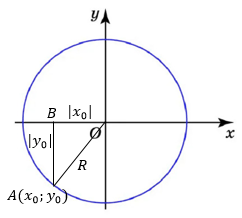Рис.2. Окружность с центром в начале координат радиуса R

Построим в системе координат окружность с центром в начале координат радиуса $R$(рис. 2). Отметим на окружности точку $A.$ Пусть точка $A$ имеет координаты $(x_0; y_0)$. Соединим центр окружности с точкой $A$. Получим отрезок $OA$, длина которого равна радиусу окружности $R$. Опустим перпендикуляр $AB$на ось $x$. Получили прямоугольный треугольник $ABO$, гипотенуза которого $AO=R$, а катеты 

$AB=\left|y_0\right|$, $BO=\left|x_0\right|$.  Длины сторон прямоугольного треугольника, как вам известно, связаны с помощью теоремы Пифагора: $B{O}^2+A{B}^2=A{O}^2$. Таким образом, имеем, что $|x_0{|}^2+|y_0{|}^2=R^2$ или $x_0^2+y_0^2=R^2$.

Так как точку на окружности мы выбрали произвольным образом, то получившееся равенство верно для любой точки, принадлежащей окружности и имеющей координаты $(x; y)$.

Таким образом, уравнением окружности с центром в начале координат и радиусом $R$ служит уравнение вида $x^2+y^2=R^2$.

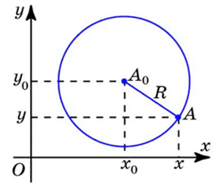Рис. 3. График окружности (x-x₀)²+(y-y₀)²=R²

Известно, что параллельный перенос применим для графика любой функции, значит, можно применить сдвиги вдоль осей $x$ и $y$ для центра окружности. Тогда уравнение окружности с центром в точке $A_0(x_0; y_0)$ и радиусом $R$ (рис. 3) имеет вид $(x-x_0{)}^2+(y-y_0{)}^2=R^2$.

Написать уравнение окружности с центром в точке $A_0(-1; 2)$ и радиусом $R=3$ и построить график этой окружности.

Рис. 4. График окружности 
(x + 1)² + (y – 2)² = 9

Решение

 

Подставив в уравнение окружности $(x-x_0{)}^2+(y-y_0{)}^2=R^2$ значения координат центра и радиуса окружности, получим 

 

$(x-(-1){)}^2+(y-2{)}^2=3^2$

$(x+1{)}^2+(y-2{)}^2=9$

 

Для того, чтобы построить окружность в координатной плоскости, нужно отметить центр в точке $A_0(-1; 2)$, а далее с помощью циркуля нарисовать окружность, радиус которой будет равен 3 (рис. 4).

 

Ответ: $(x+1{)}^2+(y-2{)}^2=9$.

Ответы

Упражнение 1

 

1. а, в, г. 2. 5.

 

Упражнение 2

 

1. $(x-2{)}^2+(y-3{)}^2=25$. 

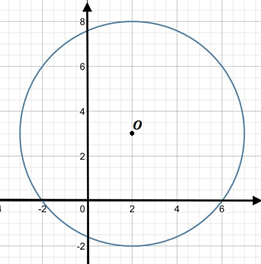
2.