Конспект урока: Бином Ньютона

Большое количество выдающихся ученых внесли свой вклад в развитие комбинаторики. Одним из них был Исаак Ньютон и его бином. Часто это понятие употребляют в литературе, в повседневной жизни. Когда хотят подчеркнуть, что собеседник преувеличивает сложность задач, с которыми он столкнулся, говорят: «Тоже мне бином Ньютона!», т.е. что вот бином Ньютона — это сложно, а у тебя что за проблемы. Так что же это за формула? В теории многочленов часто двучлены называют биномами. 

Пусть дан бином $a+b \left(\right(a+b)\ne 0)$. Рассмотрим его целые неотрицательные степени:

${(a+b)}^0=1$,

${(a+b)}^1=1\times a+1\times b$,

${(a+b)}^2=1\times a^2+2ab+1\times b^2$,

${(a+b)}^3=1\times a^3+3a^{2}b+3a{b}^2+1\times b^3$,

${(a+b)}^4={(a+b)}^3{(a+b)}^1=1\times a^4+4a^{3}b+6a^2{b}^2+4a{b}^3+1\times b^4$,

${(a+b)}^5={(a+b)}^4{(a+b)}^1=1\times a^5+5a^{4}b+10a^3{b}^2+10a^2{b}^3+5a{b}^4+1\times b^5$, 

и т. д..

Таким образом можно доказать следующую формулу

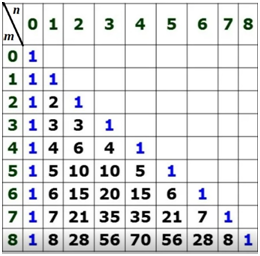Рис. 1. Фрагмент треугольника Паскаля

Для биномиальных коэффициентов ${С}_m^n$ на основании рекуррентного свойства числа сочетаний

 

${С}_m^n\mathit{+}{С}_{\mathit{m}}^{\mathit{n}\mathit{+}\mathit{1}}\mathit{=}{С}_{\mathit{m}\mathit{+}\mathit{1}}^{\mathit{n}\mathit{+}\mathit{1}}$ 

 

и с учетом, что ${С}_m^0={С}_m^n=1$ можно составить таблицу их значений, которую называют треугольником Паскаля (Рис.1). 

 

Найдем биномиальные коэффициенты при $m=4$: в предыдущей строке коэффициенты 
$1$, $3$, $3$, $1$, первую и последнюю единицы оставляем на своих местах, т. е. первым и последним коэффициентом будут единицы, и все коэффициенты последовательно складываем друг с другом, т. е. на втором месте — $1+3=4$, на третьем — $3+3=6$, на четвертом — $3+1=4$, получили коэффициенты $1$, $4$, $6$, $4$, $1$.

 

При $m=6$: коэффициенты предыдущей строки $1$, $5$, $10$, $10$, $5$, $1$, тогда получаем 

 

$1; 1+5=6; 5+10=15; 10+10=20; 10+5=15; 5+1=6; 1$.

 

Треугольник Паскаля наглядно иллюстрирует свойство числа сочетаний ${С}_m^n={С}_m^{m-n}$. Его можно сформулировать так: числа, одинаково удаленные от концов строки треугольника Паскаля, равны.

 

Вообще, при записи разложения степени бинома, нужно следить за соблюдением следующих моментов:

 

1. В полученном многочлене членов на единицу больше показателя степени бинома, т. е. если степень бинома $m$, то членов $m+1$.

2. Показатели степени первого слагаемого последовательно убывают на единицу от $m$ до $0$, а показатели второго слагаемого последовательно возрастают на единицу от $0$ до $m$.

3. Биномиальные коэффициенты, равноудаленные от начала и конца разложения по формуле (1) равны между собой.

Записать разложение бинома ${(3x-2)}^5$.

Решение

Запишем выражение ${(3x-2)}^5$ в виде ${(3x+(-2\left)\right)}^5$ и применим формулу (1):

$(3x+{(-2))}^5=C_5^0{\left(3x\right)}^5+C_5^1{\left(3x\right)}^4(-2)+C_5^2{\left(3x\right)}^3{(-2)}^2+C_5^3{\left(3x\right)}^2{(-2)}^3+$ 

$+C_5^4\left(3x\right){(-2)}^4+C_5^5{(-2)}^5=243x^5+5\times 81x^4(-2)+10\times 27x^3\times 4+$

$+10\times 9x^2(-8)+5\times 3x\times 16-32=243x^5-810x^4+1 080x^3-720x^2+240x-32$.  

Ответ: $243x^5-810x^4+1 080x^3-720x^2+240x-32$.

Возвести в степень ${(2-\sqrt{3})}^5$.

Решение

Запишем выражение ${(2-\sqrt{3})}^5$ в виде ${(2+(-\sqrt{3}\left)\right)}^5$ и применим формулу (1):

${(2+(-\sqrt{3}\left)\right)}^5=C_5^0\times 2^5+{С}_5^1\times 2^4(-\sqrt{3})+{С}_5^2\times 2^3{(-\sqrt{3})}^2+{С}_5^3\times 2^2{(-\sqrt{3})}^3+$

$+{С}_5^4\times 2{(-\sqrt{3})}^4+{С}_5^5{(-\sqrt{3})}^5=32-5\sqrt{3}\times 16+10\times 8\times 3-$

$-10\times 4\times 3\sqrt{3}+10\times 9-9\sqrt{3}=362-209\sqrt{3}$.  

Ответ: $362-209\sqrt{3}$.

Найти член разложения ${(x^{-\frac{1}{2}}+x^{\frac{1}{3}})}^{20}$, содержащий $x^5$.

Решение

Общий член разложения двадцатой степени бинома $x^{-\frac{1}{2}}+x^{\frac{1}{3}}$ имеет вид $C_{20}^n{\left(x^{-\frac{1}{2}}\right)}^{20-n}{\left(x^{\frac{1}{3}}\right)}^n$. 

Для того, чтобы некоторый член разложения содержал $x^5$ необходимо выполнение равенства ${\left(x^{-\frac{1}{2}}\right)}^{20-n}{\left(x^{\frac{1}{3}}\right)}^n=x^5$. Упростим выражение в левой части равенства. 

${\left(x^{-\frac{1}{2}}\right)}^{20-n}{\left(x^{\frac{1}{3}}\right)}^n=x^{-10+\frac{5}{6}n}$, 

т. е. нужно решить уравнение $x^{-10+\frac{5}{6}n}=x^5$, откуда $-10+\frac{5}{6}n=5$, $n=18$.

При $n=18$ имеем $C_{20}^{18}=\frac{20!}{18!\times 2!}=190$.

Ответ: $190x^5$.

1. Записать разложение бинома ${(2-a)}^6$.

2. Возвести в степень ${(1+\sqrt{6})}^4$.

3. Найти член разложения ${(c^{\frac{1}{4}}+c^{\frac{1}{2}})}^{14}$, содержащий $c^6$.

Упражнение 

1. $64-192a+240a^2-160a^3+60a^4-12a^5+a^6$.

2. $73+28\sqrt{6}$.

3. $1 001c^6$.