- Разложение вектора по двум неколлинеарным векторам
- Координаты вектора
- Знать понятие координатные векторы, чему равны координаты координатных векторов, лемму о коллинеарных векторах, утверждение о разложении произвольного вектора по координатным векторам, правила нахождения координат суммы и разности векторов, а также произведения вектора на число по заданным координатам векторов.
- Уметь доказывать: лемму о коллинеарных векторах, теорему о разложении вектора по двум неколлинеарным векторам, утверждение о разложении произвольного вектора по координатным векторам, правила нахождения координат суммы и разности векторов, а также произведения вектора на число по заданным координатам векторов.
- Уметь объяснять, что значит разложить вектор по двум данным векторам, как связаны между собой координаты равных векторов.
- Уметь находить координаты вектора, применяя правила нахождения координат суммы и разности векторов, координат произведения вектора на число.
- Какой вектор называется произведением данного вектора на число?
- Чему равно произведение , если: , ?
- Могут ли векторы и быть неколлинеарными?
- Сформулируйте основные свойства умножения вектора на число.
Разложение вектора по двум неколлинеарным векторам
Вспомним, что при умножении вектора на число мы получаем два коллинеарных вектора, которые либо сонаправлены, если , либо противоположно направлены, если . Длины векторов различаются в раз.
Справедливо и обратное суждение, которое отражено в лемме (лемма – вспомогательная теорема, с помощью которой доказывается следующая теорема или несколько теорем):
Лемма
Если векторы и коллинеарны и , то существует такое число что .
Доказательство
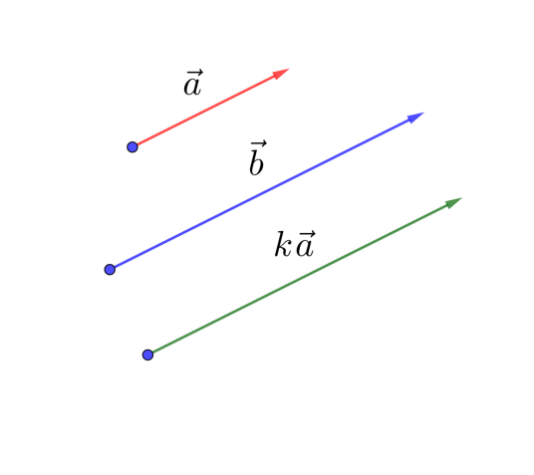 Рис. 1
Рис. 1
Рассмотрим коллинеарные векторы и Существует два случая: и либо сонаправлены, либо противоположно направлены.
1) . Возьмём число , равное отношению длин векторов
. Так как , то ,
следовательно, и их длины равны: (рис. 1). Таким образом, .
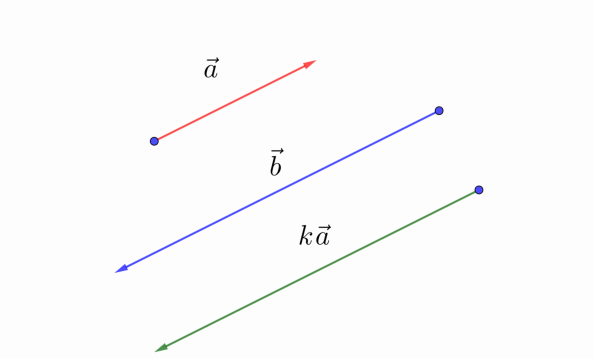 Рис. 2
Рис. 2
2) . Возьмём число , равное . Так как , то , но и их длины равны:
(рис. 2). Таким образом, Лемма доказана.
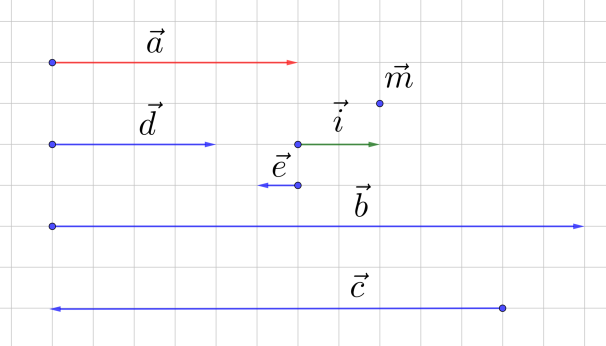 Рис. 3. Пример 1
Рис. 3. Пример 1
Пример 1
Выразить коллинеарные векторы , и через коллинеарный им вектор (рис. 3).
Решение
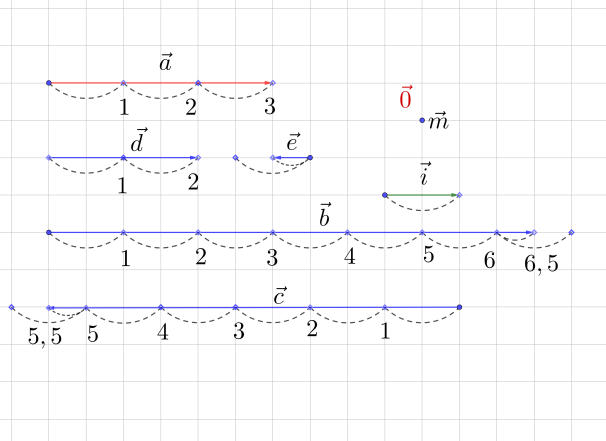 Рис. 4. Пример 1. Решение
Рис. 4. Пример 1. Решение
1. Рассмотрим векторы и : . Значит, . Взяв длину вектора за единицу (рис. 4), видим, что длина вектора в 3 раза больше, т.е.
2. Рассмотрим векторы и : Значит, . При этом длина вектора в 6,5 раз больше длины вектора , т.е.
3. Рассмотрим вектор . Он противоположно направлен вектору . Поэтому . К тому же длина вектора в 5,5 раз больше длины вектора . Значит,
4. Рассмотрим вектор : – нулевой вектор. Нам известно, что нулевой вектор сонаправлен любому вектору. И его длина равна нулю. Таким образом, вектор .
Ответ: ; ; ; .
Вспомним правило параллелограмма сложения двух векторов. Если векторы-слагаемые и отложены от одной точки, то, построив на них параллелограмм , мы получим вектор – их сумму. Обозначим вектор как вектор . Тогда, = + . В свою очередь вектор всегда можно выразить как произведение коллинеарного ему вектора на некоторое число а вектор – как произведение коллинеарного ему вектора на некоторое число . Тогда можно записать, что . В таком случае говорят, что вектор разложен по неколлинеарным векторам и , а числа и называются коэффициентами разложения.
Теорема
На плоскости любой вектор можно разложить по двум данным неколлинеарным векторам, причём коэффициенты разложения определяются единственным образом.
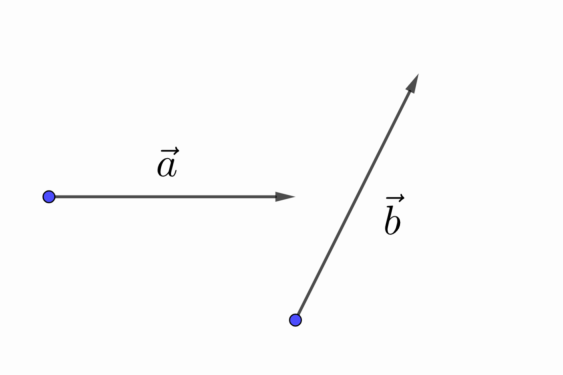 Рис. 5
Рис. 5
Доказательство
Пусть данными векторами будут неколлинеарные векторы и (рис. 5). Докажем, что любой вектор можно разложить по данным векторам.
1. Пусть . Тогда по лемме о двух коллинеарных векторах получаем, что вектор , где – некоторое число. Также можно записать его разложение в виде . Коэффициент разложения при векторе равен нулю, таким образом, вектор разложен по векторам и .
 Рис. 6
Рис. 6
2. Пусть (рис. 6): отметим некоторую точку и отложим от неё векторы , и равные векторам , и соответственно. Через точку проведём прямую, параллельную прямой . Точку пересечения полученной прямой с обозначим как .
По правилу треугольника вектор . Вектор коллинеарен вектору , вектор коллинеарен вектору . Это значит, что вектор , а вектор . Отсюда получаем, что вектор Тем самым мы разложили его по векторам и .
Первая часть теоремы доказана. Действительно, на плоскости любой вектор можно разложить по двум данным неколлинеарным векторам.
Теперь докажем, что коэффициенты разложения и определяются единственным способом.
Допустим, что кроме разложения возможно другое разложение, . Вычтем второе равенство из первого. Получаем, что нулевой вектор можно разложить по векторам и , при этом коэффициенты разложения равны и , т. е. . Такое возможно только в том случае, если данные коэффициенты разложения равны нулю. Тогда и . Значит, коэффициенты разложения определяются единственным способом.
Пример 2
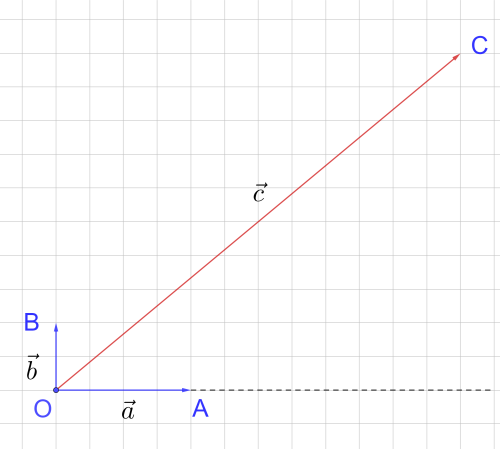 Рис. 7. Пример 2
Рис. 7. Пример 2
Разложите вектор по векторам и (рис. 7).
Решение
Все векторы отложены от точки O. При этом векторы , и равны векторам , и соответственно.
Через точку C проведём прямую, параллельную OB. И точку пересечения этой прямой с ОА назовём A1.
По правилу треугольника вектор . Вектор , тогда его можно выразить
Аналогично, выразим : , .
Тогда разложение вектора по векторам и :
Ответ:
Пример 3
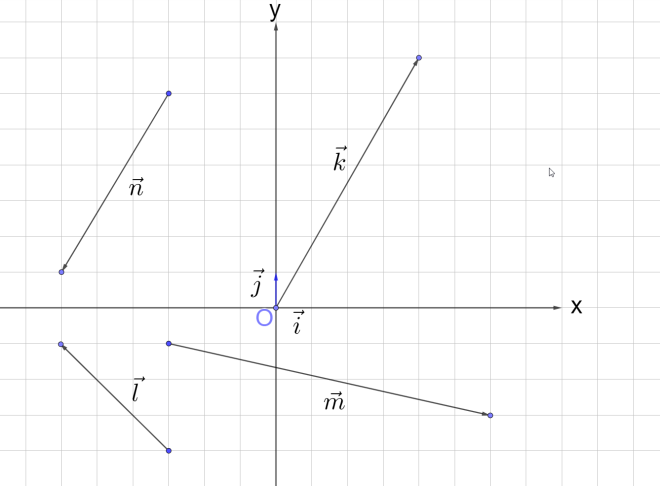 Рис. 8. Пример 3
Рис. 8. Пример 3
Разложите по двум векторам и вектор , изображённый в координатной плоскости (рис. 8).
Решение
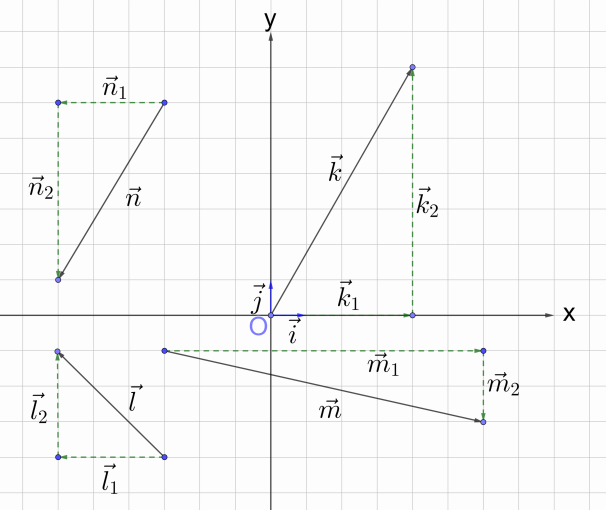 Рис. 9. Пример 3. Решение
Рис. 9. Пример 3. Решение
Итак, рассмотрим . Восстановим для него правило треугольника сложения двух векторов так, чтобы вектор являлся вектором суммы, а векторы-слагаемые и были коллинеарны векторам и соответственно.
Таким образом, = , а = . Поэтому = + .
Ответ:
Координаты вектора
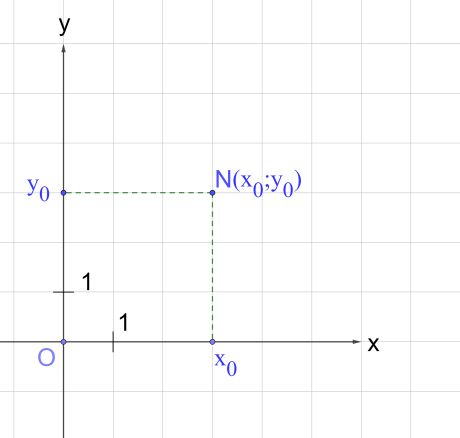 Рис. 10. Прямоугольная система координат
Рис. 10. Прямоугольная система координат
Из курса алгебры нам известна прямоугольная система координат. В ней есть оси и , а каждая отмеченная на плоскости точка имеет свои координаты, например (рис. 10) точка . Используя эти координаты, можно свести решение многих геометрических задач к работе с чисто алгебраическими уравнениями. Естественно, что на координатной плоскости можно отметить и векторы.
Построим два вектора, которые начинаются в начале координат, имеют длину, равную единице, и направления которых совпадают с направлениями осей координат. Тот вектор, который лежит на оси , обозначим буквой , а тот, который лежит на оси , обозначим как .
Векторы и называют координатными векторами.
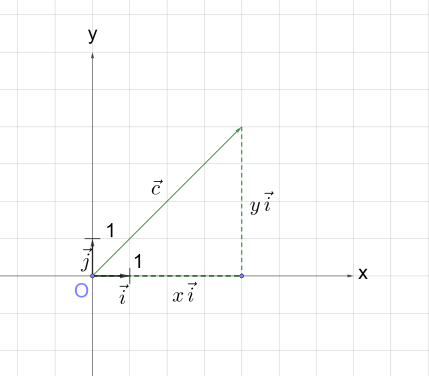 Рис. 11
Рис. 11
Понятно, что любой вектор можно разложить по векторам и . Причём коэффициенты разложения, числа и , определяются единственным образом (рис. 11), т.е. .
Коэффициенты разложения вектора по координатным векторам называют координатами вектора в данной системе координат.
Координаты вектора записывают в фигурных скобках через точку с запятой. При этом первым будем записывать коэффициент разложения , а вторым — : .
В Примере 3 мы раскладывали вектор по двум векторам и (рис. 8). Итак, вектор , следовательно, его координаты .
Коэффициенты разложения нулевого вектора по векторам и равны нулю. Тогда получаем, что
Нулевой вектор имеет координаты , причём в любой системе координат и при любых координатных векторах.
Если векторы равны, то их разложения по векторам и также будут равны, а значит, равны будут и коэффициенты разложения. Таким образом, получаем, что
Координаты равных векторов соответственно равны.
Рассмотрим ещё один особенный случай — противоположные векторы. Их разложения противоположны. Значит, противоположны будут и соответственные координаты.
Пользуясь приобретёнными знаниями о координатах вектора, получим правила нахождения координат векторов с помощью уже известных действий: сложения, вычитания и умножения вектора на число.
10. Каждая координата суммы двух и более векторов равна сумме соответствующих координат этих векторов.
Доказательство
Рассмотрим сумму двух векторов и
Пользуясь их координатами, запишем разложение данных векторов по координатным векторам: , .
Сложим полученные равенства, пользуясь свойствами сложения векторов и умножения вектора на число:
.
Координаты вектора суммы векторов и равны .
20. Каждая координата разности двух векторов равна разности соответствующих координат этих векторов.
Если и – данные векторы, то имеет координаты . Доказывается аналогично 10 свойству.
30. Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.
Доказательство
Пусть вектор имеет координаты
Найдём координаты вектора , где – произвольное число
Разложим вектор через векторы и: .
Тогда .
Таким образом, координаты вектора
Все три правила в дальнейшем помогут определять координаты любого вектора, представленного в виде алгебраической суммы данных векторов с известными координатами.
Пример 4
Найти координаты вектора , если , , , .
Решение
Представим это выражение в виде суммы. Рассмотрим отдельно каждое слагаемое:
1. Вектор имеет координаты или .
2. Вектор имеет координаты , .
3. Координаты вектора .
4. Координаты вектора .
5. Координаты вектора найдём как суммы соответствующих координат полученных векторов. В результате получаем, что имеет координаты .
Ответ: .
Упражнение 1
1. Выразите коллинеарные векторы и через коллинеарный им вектор (рис. 3).
2. Разложите по двум векторам и векторы , , и , изображённые в координатной плоскости (рис. 8).
3. Найдите координаты векторов , , и , изображённых в координатной плоскости (рис. 8).
4. Найти координаты вектора , если , , , .
Контрольные вопросы
1. Сформулируйте и докажите лемму о коллинеарных векторах.
2. Что значит разложить вектор по двум данным векторам?
3. Сформулируйте и докажите теорему о разложении вектора по двум неколлинеарным векторам.
4. Что такое координатные векторы?
5. Сформулируйте и докажите утверждение о разложении произвольного вектора по координатным векторам.
6. Что такое координаты вектора?
7. Чему равны координаты координатных векторов?
8. Как связаны между собой координаты равных векторов?
8. Сформулируйте и докажите правила нахождения координат суммы и разности векторов, произведения вектора на число по заданным координатам векторов.
Упражнение 1
1. .
2. .
3. .
4. .
- Разложение вектора по двум неколлинеарным векторам
- Координаты вектора
- Знать понятие координатные векторы, чему равны координаты координатных векторов, лемму о коллинеарных векторах, утверждение о разложении произвольного вектора по координатным векторам, правила нахождения координат суммы и разности векторов, а также произведения вектора на число по заданным координатам векторов.
- Уметь доказывать: лемму о коллинеарных векторах, теорему о разложении вектора по двум неколлинеарным векторам, утверждение о разложении произвольного вектора по координатным векторам, правила нахождения координат суммы и разности векторов, а также произведения вектора на число по заданным координатам векторов.
- Уметь объяснять, что значит разложить вектор по двум данным векторам, как связаны между собой координаты равных векторов.
- Уметь находить координаты вектора, применяя правила нахождения координат суммы и разности векторов, координат произведения вектора на число.
- Какой вектор называется произведением данного вектора на число?
- Чему равно произведение , если: , ?
- Могут ли векторы и быть неколлинеарными?
- Сформулируйте основные свойства умножения вектора на число.
Разложение вектора по двум неколлинеарным векторам
Вспомним, что при умножении вектора на число мы получаем два коллинеарных вектора, которые либо сонаправлены, если , либо противоположно направлены, если . Длины векторов различаются в раз.
Справедливо и обратное суждение, которое отражено в лемме (лемма – вспомогательная теорема, с помощью которой доказывается следующая теорема или несколько теорем):
Лемма
Если векторы и коллинеарны и , то существует такое число что .
Доказательство
 Рис. 1
Рис. 1
Рассмотрим коллинеарные векторы и Существует два случая: и либо сонаправлены, либо противоположно направлены.
1) . Возьмём число , равное отношению длин векторов
. Так как , то ,
следовательно, и их длины равны: (рис. 1). Таким образом, .
 Рис. 2
Рис. 2
2) . Возьмём число , равное . Так как , то , но и их длины равны:
(рис. 2). Таким образом, Лемма доказана.
 Рис. 3. Пример 1
Рис. 3. Пример 1
Пример 1
Выразить коллинеарные векторы , и через коллинеарный им вектор (рис. 3).
Решение
 Рис. 4. Пример 1. Решение
Рис. 4. Пример 1. Решение
1. Рассмотрим векторы и : . Значит, . Взяв длину вектора за единицу (рис. 4), видим, что длина вектора в 3 раза больше, т.е.
2. Рассмотрим векторы и : Значит, . При этом длина вектора в 6,5 раз больше длины вектора , т.е.
3. Рассмотрим вектор . Он противоположно направлен вектору . Поэтому . К тому же длина вектора в 5,5 раз больше длины вектора . Значит,
4. Рассмотрим вектор : – нулевой вектор. Нам известно, что нулевой вектор сонаправлен любому вектору. И его длина равна нулю. Таким образом, вектор .
Ответ: ; ; ; .
Вспомним правило параллелограмма сложения двух векторов. Если векторы-слагаемые и отложены от одной точки, то, построив на них параллелограмм , мы получим вектор – их сумму. Обозначим вектор как вектор . Тогда, = + . В свою очередь вектор всегда можно выразить как произведение коллинеарного ему вектора на некоторое число а вектор – как произведение коллинеарного ему вектора на некоторое число . Тогда можно записать, что . В таком случае говорят, что вектор разложен по неколлинеарным векторам и , а числа и называются коэффициентами разложения.
Теорема
На плоскости любой вектор можно разложить по двум данным неколлинеарным векторам, причём коэффициенты разложения определяются единственным образом.
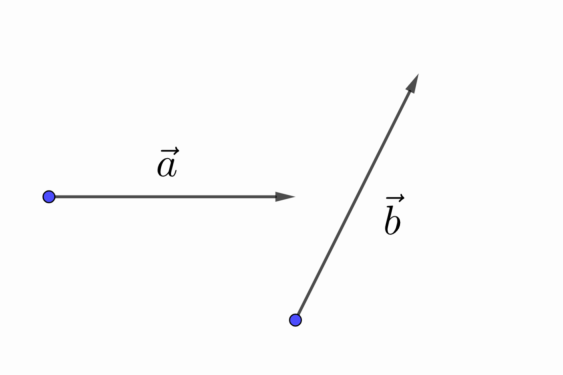 Рис. 5
Рис. 5
Доказательство
Пусть данными векторами будут неколлинеарные векторы и (рис. 5). Докажем, что любой вектор можно разложить по данным векторам.
1. Пусть . Тогда по лемме о двух коллинеарных векторах получаем, что вектор , где – некоторое число. Также можно записать его разложение в виде . Коэффициент разложения при векторе равен нулю, таким образом, вектор разложен по векторам и .
 Рис. 6
Рис. 6
2. Пусть (рис. 6): отметим некоторую точку и отложим от неё векторы , и равные векторам , и соответственно. Через точку проведём прямую, параллельную прямой . Точку пересечения полученной прямой с обозначим как .
По правилу треугольника вектор . Вектор коллинеарен вектору , вектор коллинеарен вектору . Это значит, что вектор , а вектор . Отсюда получаем, что вектор Тем самым мы разложили его по векторам и .
Первая часть теоремы доказана. Действительно, на плоскости любой вектор можно разложить по двум данным неколлинеарным векторам.
Теперь докажем, что коэффициенты разложения и определяются единственным способом.
Допустим, что кроме разложения возможно другое разложение, . Вычтем второе равенство из первого. Получаем, что нулевой вектор можно разложить по векторам и , при этом коэффициенты разложения равны и , т. е. . Такое возможно только в том случае, если данные коэффициенты разложения равны нулю. Тогда и . Значит, коэффициенты разложения определяются единственным способом.
Пример 2
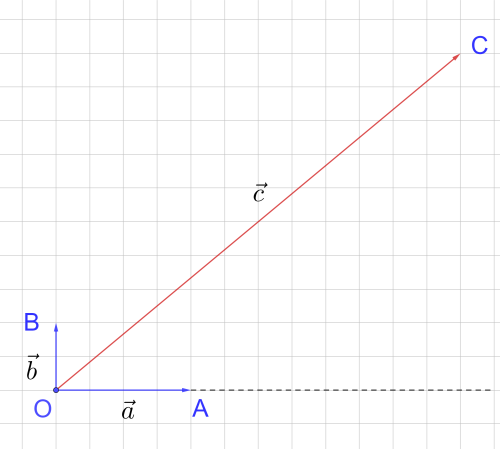 Рис. 7. Пример 2
Рис. 7. Пример 2
Разложите вектор по векторам и (рис. 7).
Решение
Все векторы отложены от точки O. При этом векторы , и равны векторам , и соответственно.
Через точку C проведём прямую, параллельную OB. И точку пересечения этой прямой с ОА назовём A1.
По правилу треугольника вектор . Вектор , тогда его можно выразить
Аналогично, выразим : , .
Тогда разложение вектора по векторам и :
Ответ:
Пример 3
 Рис. 8. Пример 3
Рис. 8. Пример 3
Разложите по двум векторам и вектор , изображённый в координатной плоскости (рис. 8).
Решение
 Рис. 9. Пример 3. Решение
Рис. 9. Пример 3. Решение
Итак, рассмотрим . Восстановим для него правило треугольника сложения двух векторов так, чтобы вектор являлся вектором суммы, а векторы-слагаемые и были коллинеарны векторам и соответственно.
Таким образом, = , а = . Поэтому = + .
Ответ:
Координаты вектора
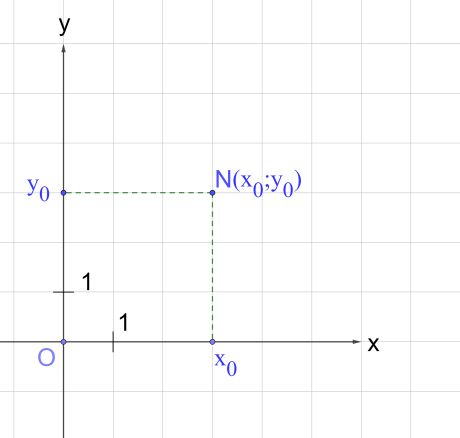 Рис. 10. Прямоугольная система координат
Рис. 10. Прямоугольная система координат
Из курса алгебры нам известна прямоугольная система координат. В ней есть оси и , а каждая отмеченная на плоскости точка имеет свои координаты, например (рис. 10) точка . Используя эти координаты, можно свести решение многих геометрических задач к работе с чисто алгебраическими уравнениями. Естественно, что на координатной плоскости можно отметить и векторы.
Построим два вектора, которые начинаются в начале координат, имеют длину, равную единице, и направления которых совпадают с направлениями осей координат. Тот вектор, который лежит на оси , обозначим буквой , а тот, который лежит на оси , обозначим как .
Векторы и называют координатными векторами.
 Рис. 11
Рис. 11
Понятно, что любой вектор можно разложить по векторам и . Причём коэффициенты разложения, числа и , определяются единственным образом (рис. 11), т.е. .
Коэффициенты разложения вектора по координатным векторам называют координатами вектора в данной системе координат.
Координаты вектора записывают в фигурных скобках через точку с запятой. При этом первым будем записывать коэффициент разложения , а вторым — : .
В Примере 3 мы раскладывали вектор по двум векторам и (рис. 8). Итак, вектор , следовательно, его координаты .
Коэффициенты разложения нулевого вектора по векторам и равны нулю. Тогда получаем, что
Нулевой вектор имеет координаты , причём в любой системе координат и при любых координатных векторах.
Если векторы равны, то их разложения по векторам и также будут равны, а значит, равны будут и коэффициенты разложения. Таким образом, получаем, что
Координаты равных векторов соответственно равны.
Рассмотрим ещё один особенный случай — противоположные векторы. Их разложения противоположны. Значит, противоположны будут и соответственные координаты.
Пользуясь приобретёнными знаниями о координатах вектора, получим правила нахождения координат векторов с помощью уже известных действий: сложения, вычитания и умножения вектора на число.
10. Каждая координата суммы двух и более векторов равна сумме соответствующих координат этих векторов.
Доказательство
Рассмотрим сумму двух векторов и
Пользуясь их координатами, запишем разложение данных векторов по координатным векторам: , .
Сложим полученные равенства, пользуясь свойствами сложения векторов и умножения вектора на число:
.
Координаты вектора суммы векторов и равны .
20. Каждая координата разности двух векторов равна разности соответствующих координат этих векторов.
Если и – данные векторы, то имеет координаты . Доказывается аналогично 10 свойству.
30. Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.
Доказательство
Пусть вектор имеет координаты
Найдём координаты вектора , где – произвольное число
Разложим вектор через векторы и: .
Тогда .
Таким образом, координаты вектора
Все три правила в дальнейшем помогут определять координаты любого вектора, представленного в виде алгебраической суммы данных векторов с известными координатами.
Пример 4
Найти координаты вектора , если , , , .
Решение
Представим это выражение в виде суммы. Рассмотрим отдельно каждое слагаемое:
1. Вектор имеет координаты или .
2. Вектор имеет координаты , .
3. Координаты вектора .
4. Координаты вектора .
5. Координаты вектора найдём как суммы соответствующих координат полученных векторов. В результате получаем, что имеет координаты .
Ответ: .
Упражнение 1
1. Выразите коллинеарные векторы и через коллинеарный им вектор (рис. 3).
2. Разложите по двум векторам и векторы , , и , изображённые в координатной плоскости (рис. 8).
3. Найдите координаты векторов , , и , изображённых в координатной плоскости (рис. 8).
4. Найти координаты вектора , если , , , .
Контрольные вопросы
1. Сформулируйте и докажите лемму о коллинеарных векторах.
2. Что значит разложить вектор по двум данным векторам?
3. Сформулируйте и докажите теорему о разложении вектора по двум неколлинеарным векторам.
4. Что такое координатные векторы?
5. Сформулируйте и докажите утверждение о разложении произвольного вектора по координатным векторам.
6. Что такое координаты вектора?
7. Чему равны координаты координатных векторов?
8. Как связаны между собой координаты равных векторов?
8. Сформулируйте и докажите правила нахождения координат суммы и разности векторов, произведения вектора на число по заданным координатам векторов.
Упражнение 1
1. .
2. .
3. .
4. .



