- Сумма двух векторов
- Законы сложения векторов. Правило параллелограмма
- Знать понятие суммы двух векторов, законы сложения векторов
- Уметь строить сумму двух данных векторов, используя правила треугольника и параллелограмма
- Дайте определение вектора
- Как обозначаются векторы?
- Что значит нулевой вектор?
- Какие векторы называются коллинеарными?
- Какие векторы являются сонаправленными, противоположно направленными?
- Какими свойствами обладают ненулевые коллинеарные векторы?
- Что называется длиной (модулем) ненулевого вектора?
- Сформулируйте определение равных векторов.
- Объясните смысл выражения: «Вектор отложен от точки A».
Сумма двух векторов
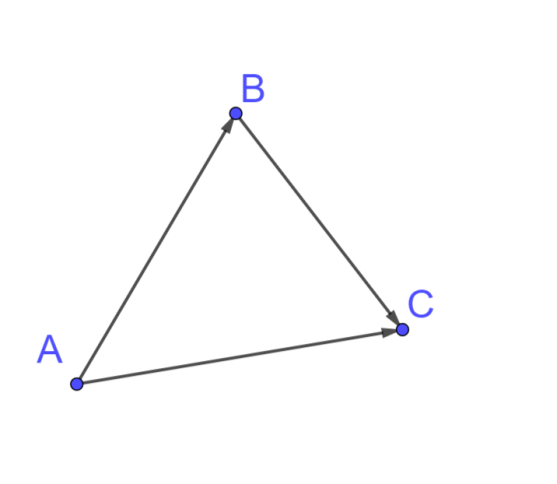 Рис. 1. Перемещение
Рис. 1. Перемещение
 Рис. 2. Сумма двух неколлинеарных векторов
Рис. 2. Сумма двух неколлинеарных векторов
Этот пример подсказывает нам универсальное правило, с помощью которого можно складывать векторы.
Его называют правилом треугольника.
С помощью правила треугольника удобно складывать векторы, если конец одного из них совпадает с началом другого. Но что делать, если это не так? В этом случае достаточно от конца одного вектора отложить вектор, равный второму (рис. 2).
Сумма векторов и обозначается так: .
Пример 1
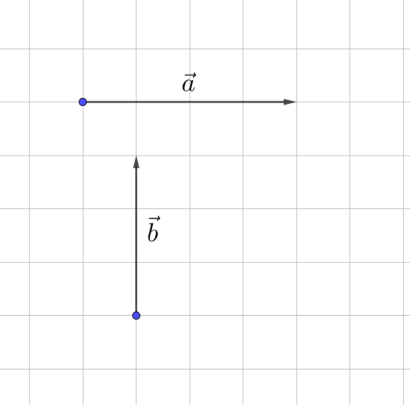 Рис. 3. Пример 1
Рис. 3. Пример 1
На рисунке изображены два вектора. Постройте их сумму и найдите длину получившегося вектора. Длина клетки 1 ед.
Решение
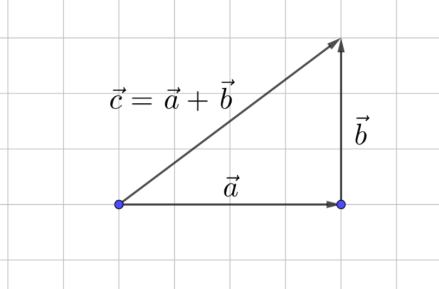 a и b" loading="lazy" />
Рис. 4. Сумма векторов a и b
a и b" loading="lazy" />
Рис. 4. Сумма векторов a и b
2. По правилу треугольника найдём сумму и , обозначим полученный вектор (рис. 4).
3. Найдём длину получившегося вектора: c — гипотенуза в прямоугольном треугольнике, длины катетов в этом треугольнике составляют 3 и 4.
Тогда по теореме Пифагора:
Ответ: 5.
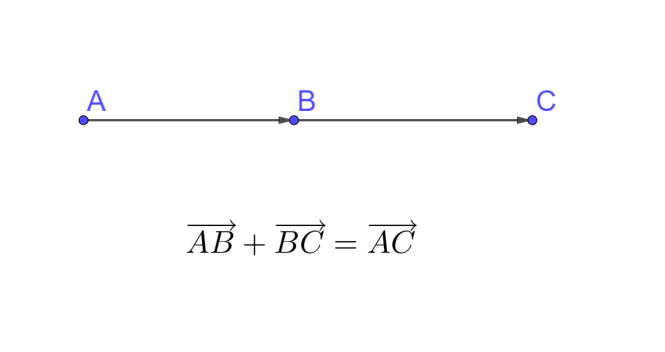 Рис. 5. Сумма двух сонаправленных векторов
Рис. 5. Сумма двух сонаправленных векторов
Отдельно рассмотрим случаи, когда складываются коллинеарные векторы. В таком случае получающаяся сумма окажется коллинеарной каждому слагаемому.
Если векторы сонаправлены, то длина итогового вектора окажется равной сумме длин складываемых векторов (рис. 5).
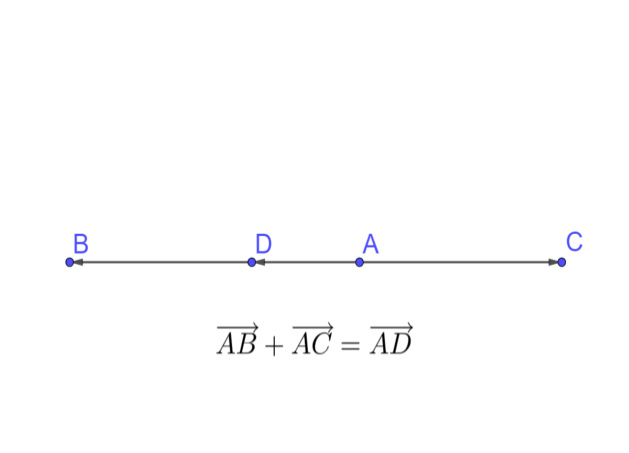 Рис. 6. Сумма двух противоположно направленных векторов
Рис. 6. Сумма двух противоположно направленных векторов
Складывая по правилу треугольника произвольный вектор с нулевым вектором, получаем, что для любого вектора справедливо равенство .
Правило треугольника можно сформулировать и следующим образом: если , и – произвольные точки, то
.
Это равенство справедливо и в случае, если две из них или даже три совпадают
Пример 2
Лодка развивает в неподвижной воде скорость 8 км/ч. Она плывет по реке, скорость течения которой составляет 2 км/ч. Найдите скорость лодки относительно берега, если: а) лодка плывет по течению реки;
б) лодка плывет против течения реки.
Решение
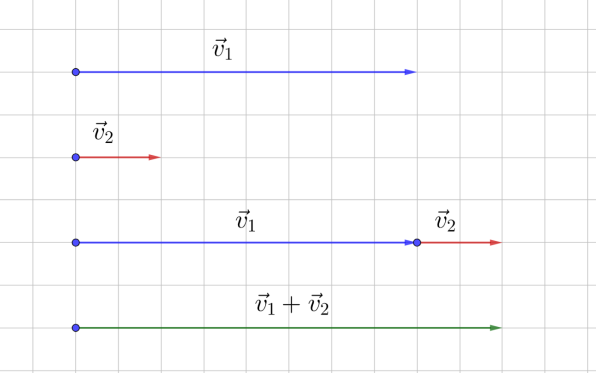 Рис. 7. Скорость лодки по течению
Рис. 7. Скорость лодки по течению
Во всех случаях итоговая скорость судна является векторной суммой собственной скорости лодки и течения реки. Однако направления этих векторов различны. Найдем решение графически. Пусть – скорость лодки, – скорость течения реки. Длина одной клетки – 1 км/ч.
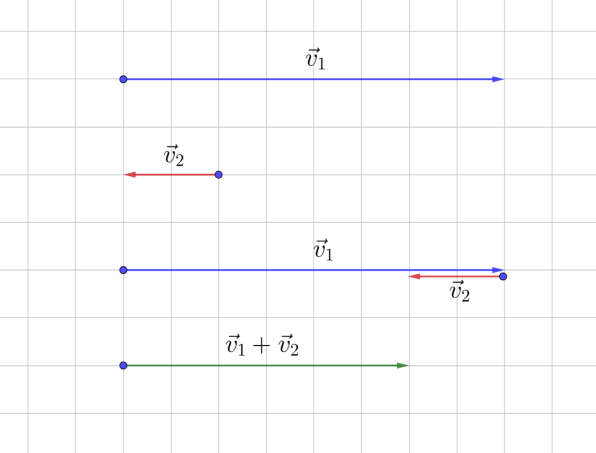 Рис. 8. Скорость лодки против течения
Рис. 8. Скорость лодки против течения
2. Во втором случае векторы уже окажутся противоположно направленными. Отрезок, соответствующий итоговой скорости, здесь уже равен 6 клеткам, значит, итоговая скорость составляет 6 км/ч (рис. 8).
Ответ: а) 10 км/ч; б) 6 км/ч.
Результат сложения (суммы) векторов и не зависит от выбора точки, от которой откладывается вектор .
Законы сложения векторов. Правило параллелограмма
Действия с векторами во многом подобны действиям с обычными числами.
Теорема
Для любых векторов , и справедливы равенства:
10. (переместительный закон);
20. (сочетательный закон).
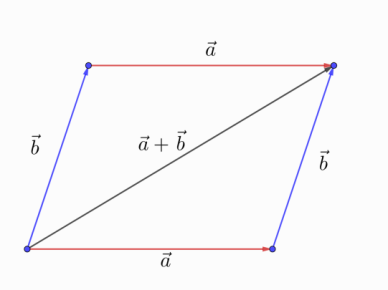 Рис. 9. Переместительный закон
Рис. 9. Переместительный закон
Итак,
Убедиться в этом можно, построив параллелограмм, сторонами которого являются складываемые векторы и (рис. 9). Видно, что по правилу треугольника диагональ параллелограмма является суммой векторов, которые соответствуют нижней и крайней правой его стороне. Стороны обозначены как векторы и , причем в данном случае к прибавляется .
Но также полученная диагональ – это сумма векторов, которые соответствуют крайней левой и его верхней стороне. Знаем, что противоположные стороны параллелограмма равны и параллельны, поэтому они и обозначены тоже векторами и соответственно. В этом случае уже к прибавляется . Результат при этом получается одинаковый, поэтому можно записать, что .
Доказывая 10, мы увидели, как работает ещё одно правило сложения векторов, которое называется правилом параллелограмма.
Если есть два вектора, которые необходимо сложить, то можно отложить их от одной точки, а потом достроить получившуюся фигуру до параллелограмма. Диагональ, исходящая из общей начальной точки векторов, будет искомой суммой данных векторов.
 Рис. 10. Сочетательный закон
Рис. 10. Сочетательный закон
20.
Убедиться в этом можно с помощью построения, используя правило треугольника. Рассмотрим рисунок 10. Здесь оранжевый вектор – это сумма красного вектора и синего вектора .
Если к оранжевому вектору добавить зеленый , то получится фиолетовый вектор, который, таким образом, является суммой .
Голубой вектор – это сумма синего и зеленого векторов, т.е. . Видно, что фиолетовый вектор представляет собой сумму красного и голубого векторов, то есть он представляет сумму . Таким образом, мы доказали, что .
Упражнение 1
1. Лодка развивает в неподвижной воде скорость 8 км/ч. Она плывет по реке, скорость воды в которой составляет 2 км/ч. Найдите скорость лодки относительно берега, если лодка плывет перпендикулярно течению.
2. В квадрате ABCD, O − точка пересечения диагоналей, Найдите векторы, равные сумме векторов и .
Контрольные вопросы
1. Объясните, какой вектор называется суммой двух векторов. В чём заключается правило треугольника сложения двух векторов?
2. Докажите, что для любого вектора справедливо равенство .
3. Сформулируйте и докажите теорему о законах сложения векторов.
4. Сформулируйте правило параллелограмма сложения двух неколлинеарных векторов?
Упражнение 1
1.
2.
- Сумма двух векторов
- Законы сложения векторов. Правило параллелограмма
- Знать понятие суммы двух векторов, законы сложения векторов
- Уметь строить сумму двух данных векторов, используя правила треугольника и параллелограмма
- Дайте определение вектора
- Как обозначаются векторы?
- Что значит нулевой вектор?
- Какие векторы называются коллинеарными?
- Какие векторы являются сонаправленными, противоположно направленными?
- Какими свойствами обладают ненулевые коллинеарные векторы?
- Что называется длиной (модулем) ненулевого вектора?
- Сформулируйте определение равных векторов.
- Объясните смысл выражения: «Вектор отложен от точки A».
Сумма двух векторов
 Рис. 1. Перемещение
Рис. 1. Перемещение
 Рис. 2. Сумма двух неколлинеарных векторов
Рис. 2. Сумма двух неколлинеарных векторов
Этот пример подсказывает нам универсальное правило, с помощью которого можно складывать векторы.
Его называют правилом треугольника.
С помощью правила треугольника удобно складывать векторы, если конец одного из них совпадает с началом другого. Но что делать, если это не так? В этом случае достаточно от конца одного вектора отложить вектор, равный второму (рис. 2).
Сумма векторов и обозначается так: .
Пример 1
 Рис. 3. Пример 1
Рис. 3. Пример 1
На рисунке изображены два вектора. Постройте их сумму и найдите длину получившегося вектора. Длина клетки 1 ед.
Решение
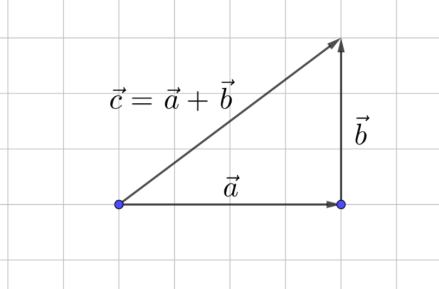 a и b" loading="lazy" />
Рис. 4. Сумма векторов a и b
a и b" loading="lazy" />
Рис. 4. Сумма векторов a и b
2. По правилу треугольника найдём сумму и , обозначим полученный вектор (рис. 4).
3. Найдём длину получившегося вектора: c — гипотенуза в прямоугольном треугольнике, длины катетов в этом треугольнике составляют 3 и 4.
Тогда по теореме Пифагора:
Ответ: 5.
 Рис. 5. Сумма двух сонаправленных векторов
Рис. 5. Сумма двух сонаправленных векторов
Отдельно рассмотрим случаи, когда складываются коллинеарные векторы. В таком случае получающаяся сумма окажется коллинеарной каждому слагаемому.
Если векторы сонаправлены, то длина итогового вектора окажется равной сумме длин складываемых векторов (рис. 5).
 Рис. 6. Сумма двух противоположно направленных векторов
Рис. 6. Сумма двух противоположно направленных векторов
Складывая по правилу треугольника произвольный вектор с нулевым вектором, получаем, что для любого вектора справедливо равенство .
Правило треугольника можно сформулировать и следующим образом: если , и – произвольные точки, то
.
Это равенство справедливо и в случае, если две из них или даже три совпадают
Пример 2
Лодка развивает в неподвижной воде скорость 8 км/ч. Она плывет по реке, скорость течения которой составляет 2 км/ч. Найдите скорость лодки относительно берега, если: а) лодка плывет по течению реки;
б) лодка плывет против течения реки.
Решение
 Рис. 7. Скорость лодки по течению
Рис. 7. Скорость лодки по течению
Во всех случаях итоговая скорость судна является векторной суммой собственной скорости лодки и течения реки. Однако направления этих векторов различны. Найдем решение графически. Пусть – скорость лодки, – скорость течения реки. Длина одной клетки – 1 км/ч.
 Рис. 8. Скорость лодки против течения
Рис. 8. Скорость лодки против течения
2. Во втором случае векторы уже окажутся противоположно направленными. Отрезок, соответствующий итоговой скорости, здесь уже равен 6 клеткам, значит, итоговая скорость составляет 6 км/ч (рис. 8).
Ответ: а) 10 км/ч; б) 6 км/ч.
Результат сложения (суммы) векторов и не зависит от выбора точки, от которой откладывается вектор .
Законы сложения векторов. Правило параллелограмма
Действия с векторами во многом подобны действиям с обычными числами.
Теорема
Для любых векторов , и справедливы равенства:
10. (переместительный закон);
20. (сочетательный закон).
 Рис. 9. Переместительный закон
Рис. 9. Переместительный закон
Итак,
Убедиться в этом можно, построив параллелограмм, сторонами которого являются складываемые векторы и (рис. 9). Видно, что по правилу треугольника диагональ параллелограмма является суммой векторов, которые соответствуют нижней и крайней правой его стороне. Стороны обозначены как векторы и , причем в данном случае к прибавляется .
Но также полученная диагональ – это сумма векторов, которые соответствуют крайней левой и его верхней стороне. Знаем, что противоположные стороны параллелограмма равны и параллельны, поэтому они и обозначены тоже векторами и соответственно. В этом случае уже к прибавляется . Результат при этом получается одинаковый, поэтому можно записать, что .
Доказывая 10, мы увидели, как работает ещё одно правило сложения векторов, которое называется правилом параллелограмма.
Если есть два вектора, которые необходимо сложить, то можно отложить их от одной точки, а потом достроить получившуюся фигуру до параллелограмма. Диагональ, исходящая из общей начальной точки векторов, будет искомой суммой данных векторов.
 Рис. 10. Сочетательный закон
Рис. 10. Сочетательный закон
20.
Убедиться в этом можно с помощью построения, используя правило треугольника. Рассмотрим рисунок 10. Здесь оранжевый вектор – это сумма красного вектора и синего вектора .
Если к оранжевому вектору добавить зеленый , то получится фиолетовый вектор, который, таким образом, является суммой .
Голубой вектор – это сумма синего и зеленого векторов, т.е. . Видно, что фиолетовый вектор представляет собой сумму красного и голубого векторов, то есть он представляет сумму . Таким образом, мы доказали, что .
Упражнение 1
1. Лодка развивает в неподвижной воде скорость 8 км/ч. Она плывет по реке, скорость воды в которой составляет 2 км/ч. Найдите скорость лодки относительно берега, если лодка плывет перпендикулярно течению.
2. В квадрате ABCD, O − точка пересечения диагоналей, Найдите векторы, равные сумме векторов и .
Контрольные вопросы
1. Объясните, какой вектор называется суммой двух векторов. В чём заключается правило треугольника сложения двух векторов?
2. Докажите, что для любого вектора справедливо равенство .
3. Сформулируйте и докажите теорему о законах сложения векторов.
4. Сформулируйте правило параллелограмма сложения двух неколлинеарных векторов?
Упражнение 1
1.
2.



