- Угол между векторами
- Скалярное произведение векторов
- Скалярное произведение в координатах
- Свойства скалярного произведения векторов
- Знать понятие угла между векторами
- Уметь находить угол между векторами на чертеже
- Знать определение скалярного произведения двух векторов
- Уметь находить скалярное произведение двух векторов
- Знать формулу скалярного произведения в координатах
- Уметь применять формулу скалярного произведения в координатах
- Знать следствия из теоремы о скалярном произведении, свойства скалярного произведения
- Уметь доказывать свойства скалярного произведения
- Что такое вектор?
- Перечислите действия, которые мы можем выполнять с векторами.
- Какой вектор называется нулевым вектором?
- Какие векторы называются коллинеарными? Сонаправленными? Противоположно направленными?
Угол между векторами
Любую пару векторов можно отложить от одной точки. Если векторы не являются сонаправленными, то они образуют некоторый угол. Этот угол называют углом между векторами.
Углом между ненулевыми векторами и называется угол, образованный при откладывании этих векторов от одной точки, и обозначается или .
Если векторы сонаправлены, то угол между ними равен 0°, а если противоположно направлены, то угол между ними равен 180°.
Пример 1
Определить угол между векторами и , изображенными на рисунке 1.
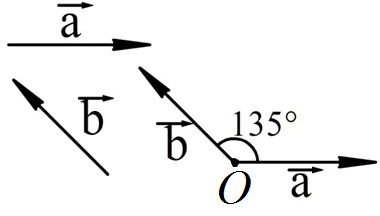 Рис. 1. Пример 1
Рис. 1. Пример 1
Решение
Чтобы определить угол между векторами и , нужно отложить их от одной точки О. Получившийся угол можно измерить с помощью транспортира. В нашем примере получилось 135°. Таким образом,
Ответ:
Два вектора называются перпендикулярными, если угол между ними равен 90°.
Вектор перпендикулярен вектору обозначается так: .
Скалярное произведение векторов
Ранее мы уже рассмотрели сложение векторов и умножение вектора на число. Введём новое действие над векторами – скалярное умножение.
Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними и обозначается или . Т.е.
Скалярное произведение - это некоторое число. Рассмотрим более подробно его значения.
Это означает, что скалярное произведение равно нулю тогда и только тогда, когда векторы перпендикулярны. Действительно, если векторы и взаимно перпендикулярны, то угол между ними равен 90°, а . Поэтому .
2.
Скалярное произведение – положительное число, когда угол между векторами острый.
3.
Скалярное произведение – отрицательное число, когда угол между векторами тупой.
4.
Если векторы сонаправлены, то скалярное произведение равно произведению их длин.
5.
Произведение называется скалярным квадратом вектора . Оно равно квадрату длины вектора .
Пример 2
Найдите скалярное произведение векторов и , если
Решение
Воспользуемся формулой для нахождения скалярного произведения: . Подставим числовые значения:
Ответ: 16
Пример 3
Найдите скалярное произведение векторов и , если
Решение
- Найдем длину вектора
2. Вычислим скалярное произведение векторов по формуле:
Ответ: .
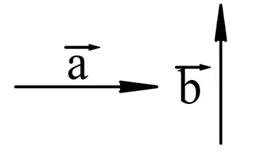 Рис. 2. Упражнение 1
Рис. 2. Упражнение 1
Упражнение 1
1. Найдите угол между векторами и на рисунке 2.
2. Найдите скалярное произведение векторов и , если
3. Найдите скалярное произведение векторов и , если
Скалярное произведение в координатах
Скалярное произведение также определяется и через координаты.
Теорема
В прямоугольной системе координат скалярное произведение векторов и и находится по формуле
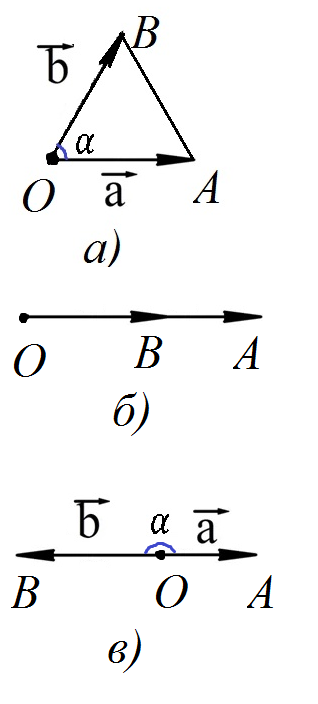 Рис. 3. Доказательство теоремы
Рис. 3. Доказательство теоремы
Доказательство
1 случай. Хотя бы один из векторов и нулевой.
Тогда доказательство очевидно, так как скалярное произведение равно нулю, а координаты нулевого вектора равны нулю.
2 случай. Векторы и ненулевые.
Отложим векторы и от точки O. Пусть .
Рассмотрим случай, когда векторы не коллинеарны (рис.3, а). По теореме косинусов
. (1)
Это равенство верно и в том случае, когда векторы и коллинеарны (см. рис. 2, б, в).
Так как то равенство (1) можно записать в другом виде:
Тогда
(2)
Векторы и имеют координаты и . Вектор будет иметь координаты . Поэтому
Подставим эти выражения в правую часть равенства (2), после преобразований получим формулу .
Теорема доказана.
Следствие 1
Ненулевые векторы и перпендикулярны тогда и только тогда, когда
Следствие 2
Косинус угла между ненулевыми векторами и выражается формулой
Пример 4
Даны векторы и . Найдите их скалярное произведение.
Решение
Воспользуемся формулой нахождения скалярного произведения через координаты .
В нашем случае получим:
Ответ: 23.
Пример 5
Проверьте, являются ли векторы и перпендикулярными.
Решение
По следствию 1 векторы перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю. Т.е.
Найдем скалярное произведение векторов и :
Таким образом, в нашем случае векторы и перпендикулярны.
Ответ: да
Пример 6
Найдите угол между векторами и
Решение
Воспользуемся формулой из следствия 2:
Подставим числовые значения:
Значит, угол между векторами равен 60°.
Ответ: 60°
Свойства скалярного произведения векторов
Есть несколько важных свойств скалярного произведения. Они очень схожи с законами алгебры, которые используются при работе с обычными числами.
Свойства
Для любых векторов и любого числа справедливы соотношения:
1°. (переместительный закон)
2°. (распределительный закон)
3°. (сочетательный закон)
4°. причем при
Свойство 1° следует из определения скалярного произведения:
и , следовательно,
Свойства 2° и 3° легко доказать. Введем прямоугольную систему координат. Пусть векторы и имеют координаты:
По формуле скалярного произведения в координатах имеем:
Свойство 2° доказано.
Рассмотрим вектор . Его координаты будут , поэтому .
Свойство 3° доказано.
Свойство 4° следует из формулы
Упражнение 2
- Даны векторы и . Найдите их скалярное произведение.
- Проверьте, являются ли векторы и перпендикулярными.
- Найдите угол между векторами и
Контрольные вопросы
- Какой угол называется углом между двумя векторами?
- Сформулируйте определение скалярного произведения двух векторов
- В каком случае скалярное произведение равно 0? меньше 0? больше 0?
- Что называют скалярным квадратом?
- Сформулируйте теорему о скалярном произведении векторов и ее следствия.
- Сформулируйте свойства скалярного произведения векторов.
Упражнение 1
1. 90°
2. -4,8.
3.
Упражнение 2
1.0
2. Нет.
3. 90°
- Угол между векторами
- Скалярное произведение векторов
- Скалярное произведение в координатах
- Свойства скалярного произведения векторов
- Знать понятие угла между векторами
- Уметь находить угол между векторами на чертеже
- Знать определение скалярного произведения двух векторов
- Уметь находить скалярное произведение двух векторов
- Знать формулу скалярного произведения в координатах
- Уметь применять формулу скалярного произведения в координатах
- Знать следствия из теоремы о скалярном произведении, свойства скалярного произведения
- Уметь доказывать свойства скалярного произведения
- Что такое вектор?
- Перечислите действия, которые мы можем выполнять с векторами.
- Какой вектор называется нулевым вектором?
- Какие векторы называются коллинеарными? Сонаправленными? Противоположно направленными?
Угол между векторами
Любую пару векторов можно отложить от одной точки. Если векторы не являются сонаправленными, то они образуют некоторый угол. Этот угол называют углом между векторами.
Углом между ненулевыми векторами и называется угол, образованный при откладывании этих векторов от одной точки, и обозначается или .
Если векторы сонаправлены, то угол между ними равен 0°, а если противоположно направлены, то угол между ними равен 180°.
Пример 1
Определить угол между векторами и , изображенными на рисунке 1.
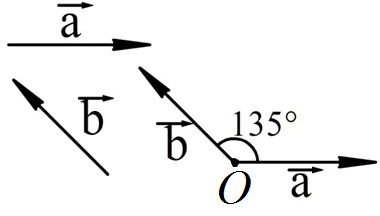 Рис. 1. Пример 1
Рис. 1. Пример 1
Решение
Чтобы определить угол между векторами и , нужно отложить их от одной точки О. Получившийся угол можно измерить с помощью транспортира. В нашем примере получилось 135°. Таким образом,
Ответ:
Два вектора называются перпендикулярными, если угол между ними равен 90°.
Вектор перпендикулярен вектору обозначается так: .
Скалярное произведение векторов
Ранее мы уже рассмотрели сложение векторов и умножение вектора на число. Введём новое действие над векторами – скалярное умножение.
Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними и обозначается или . Т.е.
Скалярное произведение - это некоторое число. Рассмотрим более подробно его значения.
Это означает, что скалярное произведение равно нулю тогда и только тогда, когда векторы перпендикулярны. Действительно, если векторы и взаимно перпендикулярны, то угол между ними равен 90°, а . Поэтому .
2.
Скалярное произведение – положительное число, когда угол между векторами острый.
3.
Скалярное произведение – отрицательное число, когда угол между векторами тупой.
4.
Если векторы сонаправлены, то скалярное произведение равно произведению их длин.
5.
Произведение называется скалярным квадратом вектора . Оно равно квадрату длины вектора .
Пример 2
Найдите скалярное произведение векторов и , если
Решение
Воспользуемся формулой для нахождения скалярного произведения: . Подставим числовые значения:
Ответ: 16
Пример 3
Найдите скалярное произведение векторов и , если
Решение
- Найдем длину вектора
2. Вычислим скалярное произведение векторов по формуле:
Ответ: .
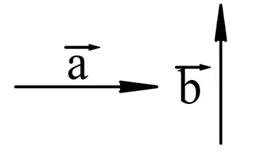 Рис. 2. Упражнение 1
Рис. 2. Упражнение 1
Упражнение 1
1. Найдите угол между векторами и на рисунке 2.
2. Найдите скалярное произведение векторов и , если
3. Найдите скалярное произведение векторов и , если
Скалярное произведение в координатах
Скалярное произведение также определяется и через координаты.
Теорема
В прямоугольной системе координат скалярное произведение векторов и и находится по формуле
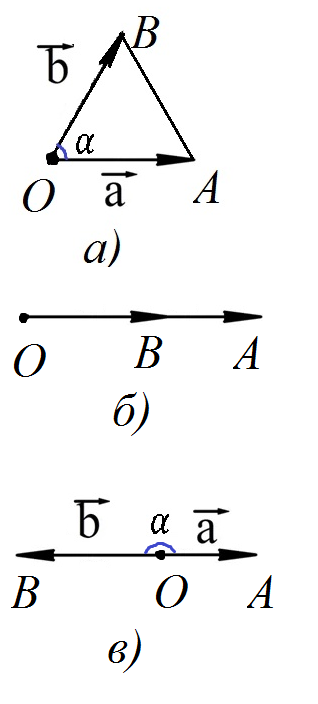 Рис. 3. Доказательство теоремы
Рис. 3. Доказательство теоремы
Доказательство
1 случай. Хотя бы один из векторов и нулевой.
Тогда доказательство очевидно, так как скалярное произведение равно нулю, а координаты нулевого вектора равны нулю.
2 случай. Векторы и ненулевые.
Отложим векторы и от точки O. Пусть .
Рассмотрим случай, когда векторы не коллинеарны (рис.3, а). По теореме косинусов
. (1)
Это равенство верно и в том случае, когда векторы и коллинеарны (см. рис. 2, б, в).
Так как то равенство (1) можно записать в другом виде:
Тогда
(2)
Векторы и имеют координаты и . Вектор будет иметь координаты . Поэтому
Подставим эти выражения в правую часть равенства (2), после преобразований получим формулу .
Теорема доказана.
Следствие 1
Ненулевые векторы и перпендикулярны тогда и только тогда, когда
Следствие 2
Косинус угла между ненулевыми векторами и выражается формулой
Пример 4
Даны векторы и . Найдите их скалярное произведение.
Решение
Воспользуемся формулой нахождения скалярного произведения через координаты .
В нашем случае получим:
Ответ: 23.
Пример 5
Проверьте, являются ли векторы и перпендикулярными.
Решение
По следствию 1 векторы перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю. Т.е.
Найдем скалярное произведение векторов и :
Таким образом, в нашем случае векторы и перпендикулярны.
Ответ: да
Пример 6
Найдите угол между векторами и
Решение
Воспользуемся формулой из следствия 2:
Подставим числовые значения:
Значит, угол между векторами равен 60°.
Ответ: 60°
Свойства скалярного произведения векторов
Есть несколько важных свойств скалярного произведения. Они очень схожи с законами алгебры, которые используются при работе с обычными числами.
Свойства
Для любых векторов и любого числа справедливы соотношения:
1°. (переместительный закон)
2°. (распределительный закон)
3°. (сочетательный закон)
4°. причем при
Свойство 1° следует из определения скалярного произведения:
и , следовательно,
Свойства 2° и 3° легко доказать. Введем прямоугольную систему координат. Пусть векторы и имеют координаты:
По формуле скалярного произведения в координатах имеем:
Свойство 2° доказано.
Рассмотрим вектор . Его координаты будут , поэтому .
Свойство 3° доказано.
Свойство 4° следует из формулы
Упражнение 2
- Даны векторы и . Найдите их скалярное произведение.
- Проверьте, являются ли векторы и перпендикулярными.
- Найдите угол между векторами и
Контрольные вопросы
- Какой угол называется углом между двумя векторами?
- Сформулируйте определение скалярного произведения двух векторов
- В каком случае скалярное произведение равно 0? меньше 0? больше 0?
- Что называют скалярным квадратом?
- Сформулируйте теорему о скалярном произведении векторов и ее следствия.
- Сформулируйте свойства скалярного произведения векторов.
Упражнение 1
1. 90°
2. -4,8.
3.
Упражнение 2
1.0
2. Нет.
3. 90°



