- Связь между координатами вектора и координатами его начала и конца
- Простейшие задачи в координатах
- Знать понятие радиус-вектора точки
- Знать формулы для нахождения координат середины отрезка, длины вектора, расстояния между двумя точками
- Уметь выводить формулу, связывающую координаты вектора с координатами его конца и начала, формулы координат середины отрезка, длины вектора и расстояния между двумя точками с известными координатами
- Уметь находить координаты вектора по координатам его начала и конца, координаты середины отрезка по координатам его начала и конца, длину вектора по его координатам, расстояние между двумя точками по их координатам
- Уметь объяснять, в чём состоит метод координат при изучении свойств геометрических фигур, решать этим методом геометрические задачи
- Запишите разложение по координатным векторам и вектора
- Запишите координаты вектора , если его разложение по координатным векторам имеет вид
- Найдите координаты вектора , равного разности векторов и , если .
- Найдите координаты вектора , если .
- Дано: . Найдите координаты вектора
Связь между координатами вектора и координатами его начала и конца
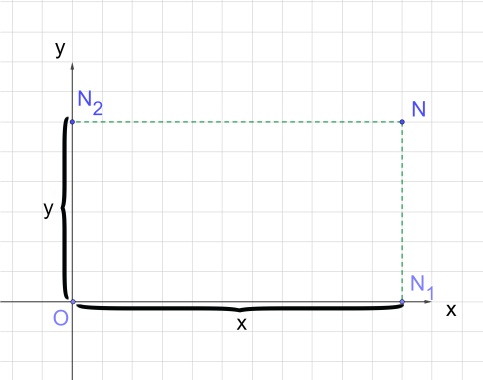 Рис. 1 . Координаты точки N
Рис. 1 . Координаты точки N
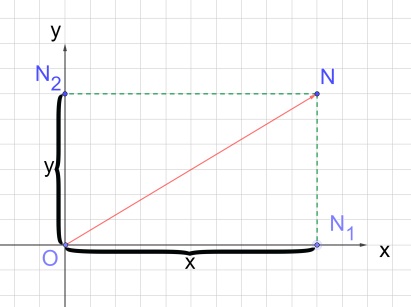 Рис. 2
Рис. 2
1. Опустим перпендикуляры из данной точки к осям координат.
2. Точки пересечения данных прямых с осями обозначим как N1 и N2.
3. Абсциссой точки N является число x, которое является длиной отрезка ОN1. А ординатой — число y, которое является длиной отрезка ОN2. N(x, y),
x = ОN1, y = ОN2 (рис. 2).
Пример 1
Определить координаты точек A, B, C, D, Е и F (рис. 3).
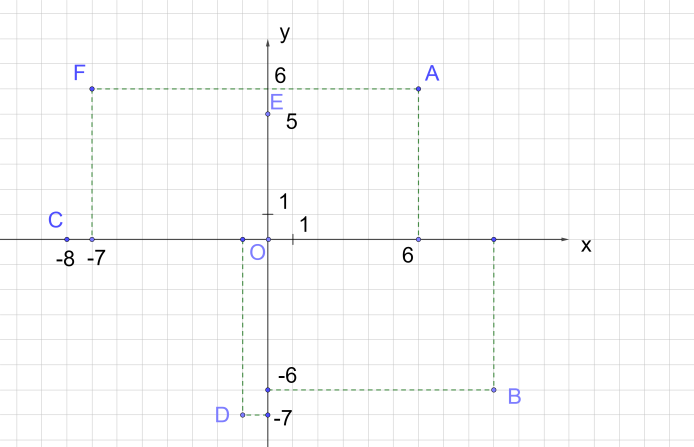 Рис. 3. Пример 1
Рис. 3. Пример 1
Решение
Проведём вектор из точки O к точке N (рис. 2).
Вектор называют радиус-вектором точки .
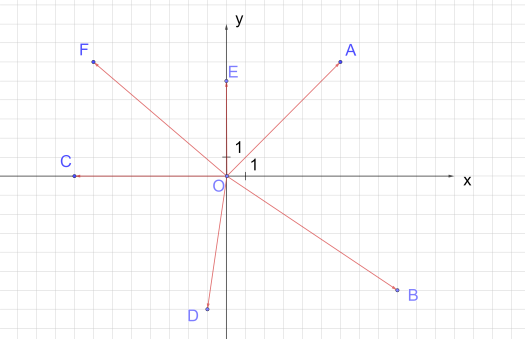 Рис. 4. Радиус-векторы
Рис. 4. Радиус-векторы
Рассмотрим рисунок 4. Для точки A радиус-вектором будет вектор , для точки B — вектор , для точки C — , для точки D — , радиус-вектором точки E является вектор , а радиус-вектором точки F — вектор .
Докажем следующее утверждение:
Координаты точки N равны соответствующим координатам её радиус-вектора.
 Рис. 5
Рис. 5
Доказательство
По правилу параллелограмма
Докажем, что вектор , а вектор . Тем самым мы докажем, что вектор
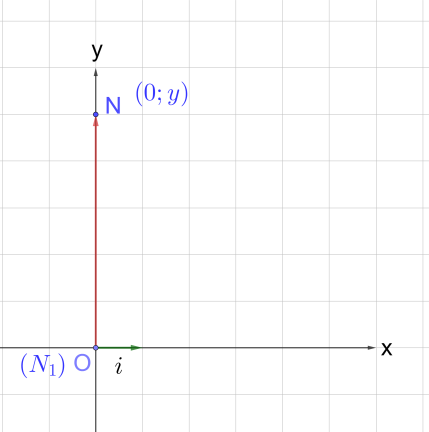 Рис. 6
Рис. 6
Если (рис. 2), то . Так как и сонаправлены, то
Если (рис. 5), то и векторы и противоположно направлены, следовательно,
Если (рис. 6), то следовательно,
Аналогично доказывается, что вектор .
Таким образом, следовательно, то есть координаты вектора такие же, как и у точки N.
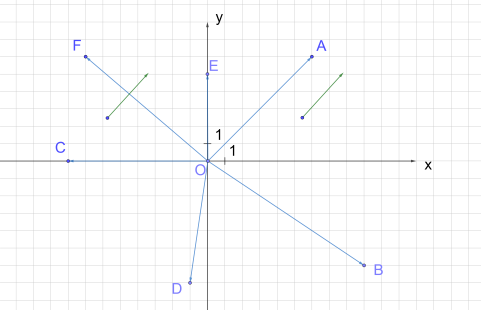 Рис. 7 Координаты векторов
Рис. 7 Координаты векторов
Вернёмся к рисункам 3 и 4: можем сказать, что координаты точки равны соответствующим координатам радиус-вектора . Значит, вектор Аналогично, вектор , , , , .
Обратите внимание, что координаты точек помогают определить их расположение в пределах координатной плоскости, а вот координаты векторов указывают на перемещение относительно осей x и y. Если взять две несовпадающие точки, то они однозначно имеют различные координаты в отличие от двух несовпадающих векторов (рис. 7).
Два несовпадающих вектора могут иметь одинаковые координаты в том случае, если векторы равны.
Итак, мы доказали, что координаты точки N равны соответствующим координатам её радиус-вектора.
Радиус-вектором точки называют вектор, начало которого совпадает с точкой начала координат, а конец — с данной точкой.
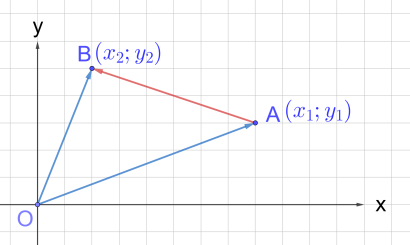 Рис. 8
Рис. 8
Пользуясь этим утверждением, выразим координаты вектора через координаты его начала и конца. Пусть точка A имеет координаты (x1; y1), а точка B имеет координаты (x2; y2). Вектор (рис. 8). А они в свою очередь являются радиус-векторами точек B и A соответственно. А это значит, что координаты вектора , а координаты вектора .
Можем найти координаты вектора разности: , . Понятно, что эти значения и будут координатами вектора Так мы доказали, что
каждая координата вектора равна разности соответствующих координат его конца и начала.
Пример 2
По координатам точек и найти координаты вектора
Решение
a)
б)
Ответ: а) б)
Простейшие задачи в координатах
Рассмотрим три вспомогательные задачи, которые будем использовать при решении геометрических задач методом координат.
Первой решим задачу на определение координат середины отрезка.
Пример 3
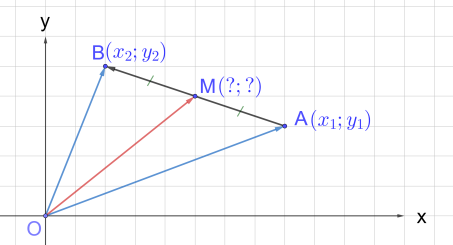 Рис. 9 Пример 3
Рис. 9 Пример 3
Решение
Воспользуемся ранее доказанным утверждением и на основании того, что M — середина AB, запишем, что вектор равен полусумме векторов и , т.е. .
Векторы и являются радиус-векторами точек A и B соответственно. Значит, координаты вектора а координаты вектора .
Вектор их суммы будет иметь координаты {x1 + x2; y1 + y2}.
Тогда координаты вектора их полусуммы равны .
Эти значения и будут координатами вектора , который, в свою очередь, является радиус-вектором точки M. А это значит, что координаты точки M равны соответствующим координатам её радиус-вектора .
Ответ: .
Таким образом, мы получили, что
Каждая координата середины отрезка равна полусумме соответствующих координат его концов.
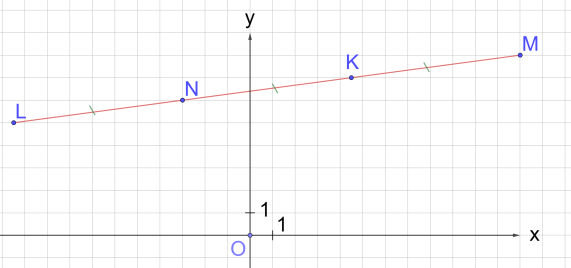 Рис. 10. Пример 4
Рис. 10. Пример 4
Пример 4
Даны точки M (12; 8) и N (-3; 6). Найти координаты точек K и L, если K — середина MN, а N — середина KL
(рис. 10).
Решение
K ; K (4,5; 7)
N:
L (-10,5; 5).
Ответ: K (4,5; 7), L (-10,5; 5).
Решим вторую вспомогательную задачу.
Пример 5
Вычислите длину вектора по его координатам.
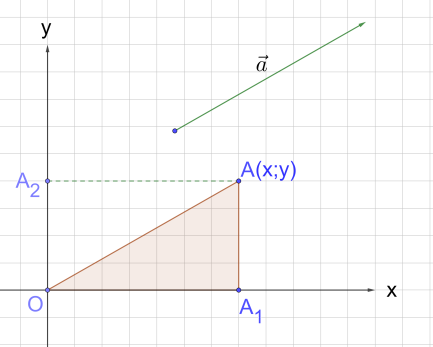 Рис. 11 Пример 5
Рис. 11 Пример 5
Решение
Пусть дан вектор . От начала координат отложим вектор равный вектору
(рис. 11).
Проведём перпендикуляры АА1 и АА2 к осям координат.
Если точка A имеет координаты (x; y), то и её радиус-вектор имеет такие же координаты. При этом координаты вектора также равны (x; y), так как
Итак, можно сказать, что длина отрезка OА1 = |x|, а длина отрезка А1А = OА2 = |y|.
Длину отрезка ОА можем выразить из прямоугольного треугольника ОА1А:
ОA2 = OА12 + А1А2;
;
.
Из того, что следует, что . Таким образом,
Получаем, что , причём от какой бы точки вектор не был бы отложен.
Ответ:
Длина вектора вычисляется по формуле
.
Пример 6
Вычислите длины векторов по их координатам, если и
Решение
Ответ: ,
Рассмотрим третью вспомогательную задачу.
Пример 7
Определите расстояние между двумя точками по их координатам.
 Рис. 12 Пример 7
Рис. 12 Пример 7
Решение
Пусть точка N1 (x1; y1), а точка N2 (x2; y2).
Выразим расстояние d между этими точками через их координаты (рис. 12).
Рассмотрим вектор . Длина этого вектора может быть найдена по формуле:
Так как то расстояние между точками N1 (x1; y1) и N2 (x2; y2) можно найти по формуле
Ответ:
Отсюда получаем, что
Расстояние между двумя точками находят как корень квадратный из суммы квадратов разностей соответствующих координат данных точек, по формуле .
Можно сказать также, что данная формула служит для нахождения длины отрезка по координатам его концов.
Пример 8
Докажите, что середина гипотенузы прямоугольного треугольника равноудалена от всех его вершин.
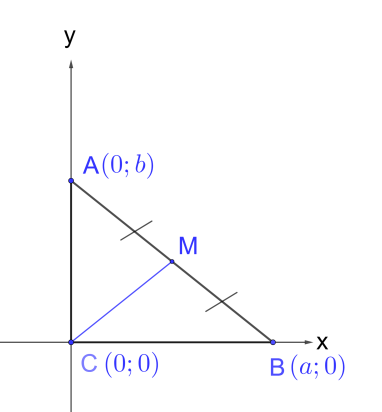 Рис. 13 Пример 8
Рис. 13 Пример 8
Доказательство
Рассмотрим треугольник ABC,
где ∠ C = 90° (рис. 13).
Обозначим буквой M середину гипотенузы AB.
Введем систему координат с началом в точке C (рис. 13):
A (0; b), B (a; 0), C (0; 0).
По формулам координат середины отрезка найдём координаты точки
По формуле расстояния между двумя точками найдем длины отрезков MC и MA:
Таким образом, MC = MA = MB.
Пример 9
Докажите, что сумма квадратов всех сторон параллелограмма равна сумме квадратов его диагоналей.
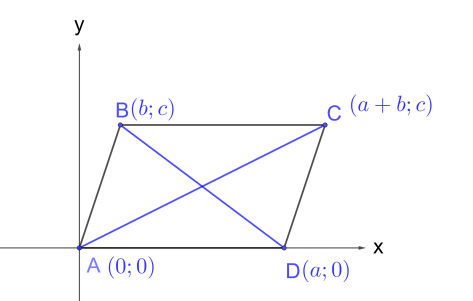 Рис. 14. Пример 9
Рис. 14. Пример 9
Доказательство
Построим параллелограмм ABCD в прямоугольной системе координат с началом в вершине A (0; 0) (рис. 14).
AD = BC = a, вершина B (b; c), точка D (a; 0), а C (a + b; c)
По формуле расстояния между двумя точками:
AB2 = b2 + c2, AD2 = a2, AC2 = (a + b)2+c2, BD2 = (a - b)2 + c2.
Получаем:
AB2 + BC2 + СD2 + DA2 = 2(AB2 + AD2) = 2(a2 + b2+c2).
AC2 + BD2 = (a + b)2+c2 + (a - b)2 + c2 = 2(a2 + b2+c2).
Таким образом, AB2 + BC2 + СD2 + DA2 = AC2 + BD2, что и требовалось доказать.
Упражнение 1
1. По координатам точек A и B найти координаты вектора :
а) A (; 0), B (0; 0); б) A (10; 4), B (5; -1); в) A (0; 0), B (-7; 1); г) A (-3; -3), B (10; 10).
2. Найдите координаты точки M, являющейся серединой отрезка AB.
|
A (x1; y1)
|
(3; 3)
|
(-4; 0)
|
(; 4)
|
(-7; 2)
|
|
B (x2; y2)
|
(1; 1)
|
(2; 15)
|
(2,5; 8)
|
(5; -2)
|
|
M (x; y)
|
( ; )
|
( ; )
|
( ; )
|
( ; )
|
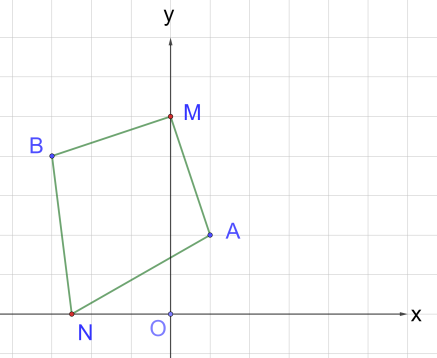 Рис. 15. Упражнение 4
Рис. 15. Упражнение 4
3. Вычислите длины векторов по их координатам, если и
4. На оси Ox и на оси Oy найти точки, равноудалённые от точек A(1; 2) и B(-3;4) (рис. 15).
Контрольные вопросы
1. Что такое радиус-вектор точки?
2. Как вычислить координаты вектора по координатам его начала и конца?
3. Как вычислить координаты середины отрезка по координатам его начала и конца?
4. Как найти длину вектора по его координатам?
5. Как вычислить расстояние между двумя точками по их координатам?
- а) , б) , в) , г) .
2.
|
A (x1; y1)
|
(3; 3)
|
(-4; 0)
|
(; 4)
|
(-7; 2)
|
|
B (x2; y2)
|
(1; 1)
|
(2; 15)
|
(2,5; 8)
|
(5; -2)
|
|
M (x; y)
|
(2; 2)
|
(-1 ; 7,5)
|
(1,5; 6)
|
(-1; 0)
|
3.
4. N (-2,5; 0), M (0; 5).
- Связь между координатами вектора и координатами его начала и конца
- Простейшие задачи в координатах
- Знать понятие радиус-вектора точки
- Знать формулы для нахождения координат середины отрезка, длины вектора, расстояния между двумя точками
- Уметь выводить формулу, связывающую координаты вектора с координатами его конца и начала, формулы координат середины отрезка, длины вектора и расстояния между двумя точками с известными координатами
- Уметь находить координаты вектора по координатам его начала и конца, координаты середины отрезка по координатам его начала и конца, длину вектора по его координатам, расстояние между двумя точками по их координатам
- Уметь объяснять, в чём состоит метод координат при изучении свойств геометрических фигур, решать этим методом геометрические задачи
- Запишите разложение по координатным векторам и вектора
- Запишите координаты вектора , если его разложение по координатным векторам имеет вид
- Найдите координаты вектора , равного разности векторов и , если .
- Найдите координаты вектора , если .
- Дано: . Найдите координаты вектора
Связь между координатами вектора и координатами его начала и конца
 Рис. 1 . Координаты точки N
Рис. 1 . Координаты точки N
 Рис. 2
Рис. 2
1. Опустим перпендикуляры из данной точки к осям координат.
2. Точки пересечения данных прямых с осями обозначим как N1 и N2.
3. Абсциссой точки N является число x, которое является длиной отрезка ОN1. А ординатой — число y, которое является длиной отрезка ОN2. N(x, y),
x = ОN1, y = ОN2 (рис. 2).
Пример 1
Определить координаты точек A, B, C, D, Е и F (рис. 3).
 Рис. 3. Пример 1
Рис. 3. Пример 1
Решение
Проведём вектор из точки O к точке N (рис. 2).
Вектор называют радиус-вектором точки .
 Рис. 4. Радиус-векторы
Рис. 4. Радиус-векторы
Рассмотрим рисунок 4. Для точки A радиус-вектором будет вектор , для точки B — вектор , для точки C — , для точки D — , радиус-вектором точки E является вектор , а радиус-вектором точки F — вектор .
Докажем следующее утверждение:
Координаты точки N равны соответствующим координатам её радиус-вектора.
 Рис. 5
Рис. 5
Доказательство
По правилу параллелограмма
Докажем, что вектор , а вектор . Тем самым мы докажем, что вектор
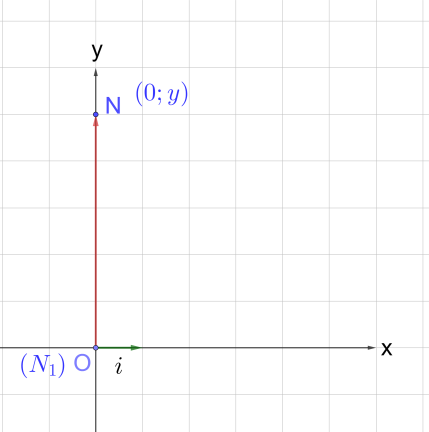 Рис. 6
Рис. 6
Если (рис. 2), то . Так как и сонаправлены, то
Если (рис. 5), то и векторы и противоположно направлены, следовательно,
Если (рис. 6), то следовательно,
Аналогично доказывается, что вектор .
Таким образом, следовательно, то есть координаты вектора такие же, как и у точки N.
 Рис. 7 Координаты векторов
Рис. 7 Координаты векторов
Вернёмся к рисункам 3 и 4: можем сказать, что координаты точки равны соответствующим координатам радиус-вектора . Значит, вектор Аналогично, вектор , , , , .
Обратите внимание, что координаты точек помогают определить их расположение в пределах координатной плоскости, а вот координаты векторов указывают на перемещение относительно осей x и y. Если взять две несовпадающие точки, то они однозначно имеют различные координаты в отличие от двух несовпадающих векторов (рис. 7).
Два несовпадающих вектора могут иметь одинаковые координаты в том случае, если векторы равны.
Итак, мы доказали, что координаты точки N равны соответствующим координатам её радиус-вектора.
Радиус-вектором точки называют вектор, начало которого совпадает с точкой начала координат, а конец — с данной точкой.
 Рис. 8
Рис. 8
Пользуясь этим утверждением, выразим координаты вектора через координаты его начала и конца. Пусть точка A имеет координаты (x1; y1), а точка B имеет координаты (x2; y2). Вектор (рис. 8). А они в свою очередь являются радиус-векторами точек B и A соответственно. А это значит, что координаты вектора , а координаты вектора .
Можем найти координаты вектора разности: , . Понятно, что эти значения и будут координатами вектора Так мы доказали, что
каждая координата вектора равна разности соответствующих координат его конца и начала.
Пример 2
По координатам точек и найти координаты вектора
Решение
a)
б)
Ответ: а) б)
Простейшие задачи в координатах
Рассмотрим три вспомогательные задачи, которые будем использовать при решении геометрических задач методом координат.
Первой решим задачу на определение координат середины отрезка.
Пример 3
 Рис. 9 Пример 3
Рис. 9 Пример 3
Решение
Воспользуемся ранее доказанным утверждением и на основании того, что M — середина AB, запишем, что вектор равен полусумме векторов и , т.е. .
Векторы и являются радиус-векторами точек A и B соответственно. Значит, координаты вектора а координаты вектора .
Вектор их суммы будет иметь координаты {x1 + x2; y1 + y2}.
Тогда координаты вектора их полусуммы равны .
Эти значения и будут координатами вектора , который, в свою очередь, является радиус-вектором точки M. А это значит, что координаты точки M равны соответствующим координатам её радиус-вектора .
Ответ: .
Таким образом, мы получили, что
Каждая координата середины отрезка равна полусумме соответствующих координат его концов.
 Рис. 10. Пример 4
Рис. 10. Пример 4
Пример 4
Даны точки M (12; 8) и N (-3; 6). Найти координаты точек K и L, если K — середина MN, а N — середина KL
(рис. 10).
Решение
K ; K (4,5; 7)
N:
L (-10,5; 5).
Ответ: K (4,5; 7), L (-10,5; 5).
Решим вторую вспомогательную задачу.
Пример 5
Вычислите длину вектора по его координатам.
 Рис. 11 Пример 5
Рис. 11 Пример 5
Решение
Пусть дан вектор . От начала координат отложим вектор равный вектору
(рис. 11).
Проведём перпендикуляры АА1 и АА2 к осям координат.
Если точка A имеет координаты (x; y), то и её радиус-вектор имеет такие же координаты. При этом координаты вектора также равны (x; y), так как
Итак, можно сказать, что длина отрезка OА1 = |x|, а длина отрезка А1А = OА2 = |y|.
Длину отрезка ОА можем выразить из прямоугольного треугольника ОА1А:
ОA2 = OА12 + А1А2;
;
.
Из того, что следует, что . Таким образом,
Получаем, что , причём от какой бы точки вектор не был бы отложен.
Ответ:
Длина вектора вычисляется по формуле
.
Пример 6
Вычислите длины векторов по их координатам, если и
Решение
Ответ: ,
Рассмотрим третью вспомогательную задачу.
Пример 7
Определите расстояние между двумя точками по их координатам.
 Рис. 12 Пример 7
Рис. 12 Пример 7
Решение
Пусть точка N1 (x1; y1), а точка N2 (x2; y2).
Выразим расстояние d между этими точками через их координаты (рис. 12).
Рассмотрим вектор . Длина этого вектора может быть найдена по формуле:
Так как то расстояние между точками N1 (x1; y1) и N2 (x2; y2) можно найти по формуле
Ответ:
Отсюда получаем, что
Расстояние между двумя точками находят как корень квадратный из суммы квадратов разностей соответствующих координат данных точек, по формуле .
Можно сказать также, что данная формула служит для нахождения длины отрезка по координатам его концов.
Пример 8
Докажите, что середина гипотенузы прямоугольного треугольника равноудалена от всех его вершин.
 Рис. 13 Пример 8
Рис. 13 Пример 8
Доказательство
Рассмотрим треугольник ABC,
где ∠ C = 90° (рис. 13).
Обозначим буквой M середину гипотенузы AB.
Введем систему координат с началом в точке C (рис. 13):
A (0; b), B (a; 0), C (0; 0).
По формулам координат середины отрезка найдём координаты точки
По формуле расстояния между двумя точками найдем длины отрезков MC и MA:
Таким образом, MC = MA = MB.
Пример 9
Докажите, что сумма квадратов всех сторон параллелограмма равна сумме квадратов его диагоналей.
 Рис. 14. Пример 9
Рис. 14. Пример 9
Доказательство
Построим параллелограмм ABCD в прямоугольной системе координат с началом в вершине A (0; 0) (рис. 14).
AD = BC = a, вершина B (b; c), точка D (a; 0), а C (a + b; c)
По формуле расстояния между двумя точками:
AB2 = b2 + c2, AD2 = a2, AC2 = (a + b)2+c2, BD2 = (a - b)2 + c2.
Получаем:
AB2 + BC2 + СD2 + DA2 = 2(AB2 + AD2) = 2(a2 + b2+c2).
AC2 + BD2 = (a + b)2+c2 + (a - b)2 + c2 = 2(a2 + b2+c2).
Таким образом, AB2 + BC2 + СD2 + DA2 = AC2 + BD2, что и требовалось доказать.
Упражнение 1
1. По координатам точек A и B найти координаты вектора :
а) A (; 0), B (0; 0); б) A (10; 4), B (5; -1); в) A (0; 0), B (-7; 1); г) A (-3; -3), B (10; 10).
2. Найдите координаты точки M, являющейся серединой отрезка AB.
|
A (x1; y1)
|
(3; 3)
|
(-4; 0)
|
(; 4)
|
(-7; 2)
|
|
B (x2; y2)
|
(1; 1)
|
(2; 15)
|
(2,5; 8)
|
(5; -2)
|
|
M (x; y)
|
( ; )
|
( ; )
|
( ; )
|
( ; )
|
 Рис. 15. Упражнение 4
Рис. 15. Упражнение 4
3. Вычислите длины векторов по их координатам, если и
4. На оси Ox и на оси Oy найти точки, равноудалённые от точек A(1; 2) и B(-3;4) (рис. 15).
Контрольные вопросы
1. Что такое радиус-вектор точки?
2. Как вычислить координаты вектора по координатам его начала и конца?
3. Как вычислить координаты середины отрезка по координатам его начала и конца?
4. Как найти длину вектора по его координатам?
5. Как вычислить расстояние между двумя точками по их координатам?
- а) , б) , в) , г) .
2.
|
A (x1; y1)
|
(3; 3)
|
(-4; 0)
|
(; 4)
|
(-7; 2)
|
|
B (x2; y2)
|
(1; 1)
|
(2; 15)
|
(2,5; 8)
|
(5; -2)
|
|
M (x; y)
|
(2; 2)
|
(-1 ; 7,5)
|
(1,5; 6)
|
(-1; 0)
|
3.
4. N (-2,5; 0), M (0; 5).



