- Понятие вектора
- Равенство векторов
- Откладывание вектора от данной точки
- Знать определения вектора, нулевого вектора, длины вектора, коллинеарных векторов, сонаправленных векторов, противоположно направленных и равных векторов
- Знать, как обозначаются коллинеарные векторы, сонаправленные и противоположно направленные векторы, длина вектора
- Уметь изображать и обозначать векторы, откладывать от данной точки вектор, равный данному.
- Установите, какие из величин характеризуются числовым значением, а какие и числовым значением, и направлением.
- температура
- масса
- скорость
- длина
- сила
- перемещение
Понятие вектора
Из физики известно, что некоторые величины характеризуются не только числовым значением, но и направлением.
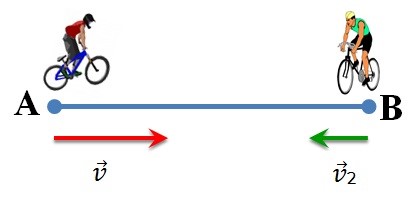 Рис. 1. Движение велосипедистов
Рис. 1. Движение велосипедистов
Величины бывают скалярными или векторными.
Скалярными называют величины, имеющие численное значение, но не имеющие направления.
Например, количество каких-нибудь предметов, длина, плотность.
Векторными величинами, или векторами, называют величины, имеющие и численное значение, и направление.
Например, если сказано, что велосипедист движется со скоростью 40 километров в час (то есть дано численное значение скорости), то про его движение известно не всё, потому что неизвестно, куда, в каком направлении он двигается. Примеры векторных величин — скорость, сила, перемещение.
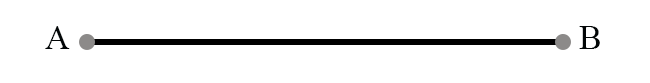 Рис. 2. Отрезок
Рис. 2. Отрезок
Рассмотрим произвольный отрезок АВ (Рис. 2). Точки А и В называют его концами или граничными точками.
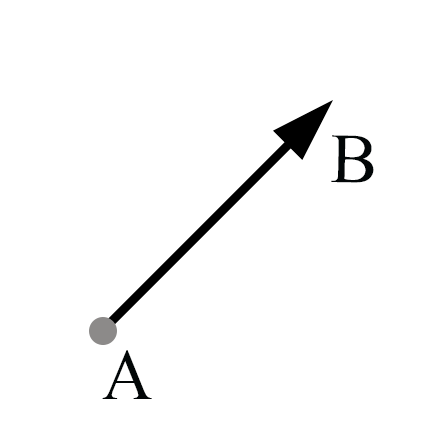 Рис. 3. Направленный отрезок
Рис. 3. Направленный отрезок
Итак, на данном отрезке можно указать два направления: от точки B к точке А и наоборот.
При выборе направления назовём одну граничную точку началом отрезка, в данном случае A, а другую — концом отрезка — B. Будем считать, что отрезок направлен от начала к концу (Рис. 3)
Отрезок, для которого указано, какая из его граничных точек считается началом, а какая — концом, называется направленным отрезком или вектором.
Вектор изображают в виде отрезка со стрелкой, показывающей направление вектора.
Вектор можно обозначить:
Двумя заглавными буквами, поставив над ними стрелочку; первая буква показывает начальную точку, вторая — конечную точку, например, − (читается: вектор AB);
Маленькой буквой со стрелочкой над ней, например, (читается: вектор a).
Если начальная и конечная точки вектора совпадают, получается нулевой вектор, который обозначается как . Любую точку на плоскости можно считать нулевым вектором.
Например, вектор, обозначенный точкой N, будет иметь название или .
Пример 1
Отметить точки M, N, K и P так, чтобы никакие 3 из них не лежали на одной прямой. Начертить все ненулевые векторы, начало и конец которых совпадают с какими-то двумя из этих точек. Выписать все полученные векторы и указать их начало и конец. Сколько векторов получилось?
Решение примера 1
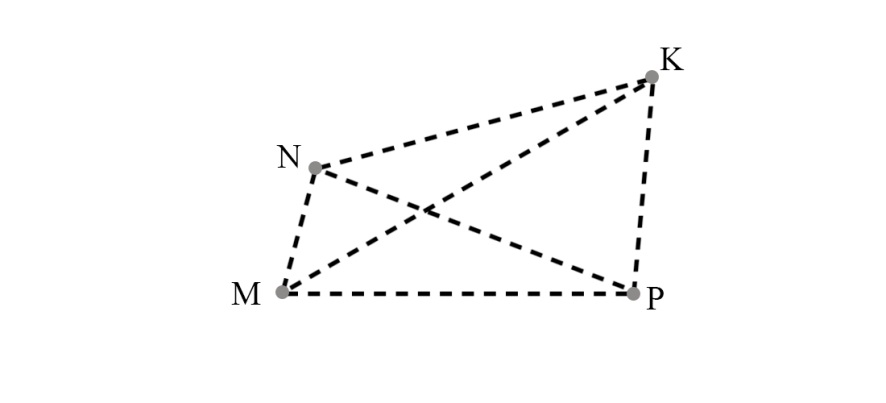 Рис. 4. Чертёж. Пример 1
Рис. 4. Чертёж. Пример 1
2. Составим таблицу, в которую будем записывать все полученные векторы, а также их начало и конец.
3. Построим искомые векторы.

Ответ: 12 векторов
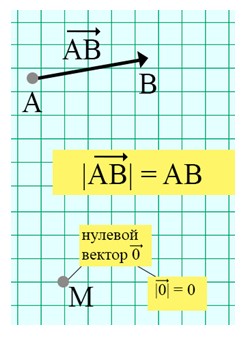 Рис. 5. Длина вектора
Рис. 5. Длина вектора
Можно говорить «модуль вектора АВ (модуль вектора а)».
При нахождении длины вектора мы не учитываем его направление.
Длина нулевого вектора равна 0:
Пример 2
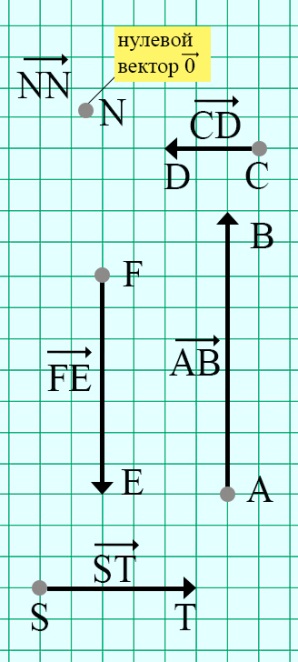 Рис. 6. Чертёж. Пример 2
Рис. 6. Чертёж. Пример 2
На рисунке 6 изображены векторы. Чему равна длина каждого вектора, если известно, что сторона клетки равна 1 см?
Решение
1. ||= || = 0 (см)
2. | | = CD = 3 (см)
3. || = FE = 7 (см)
4. || = AB = 9 (см)
5. || = ST = 5 (см)
Ответ: || = 0 см, || = 3 см, || = 7 см, || = 9 см, || = 5 см.
Равенство векторов
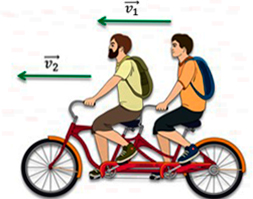 Рис. 7. Движение в тандеме
Рис. 7. Движение в тандеме
(рис.7). Каждый из них движется в одном и том же направлении и с одной и той же скоростью. Скорость каждого спортсмена является векторной величиной, соответственно, изобразим её в виде вектора. Получим, что все направленные отрезки, изображающие скорости разных точек, имеют одинаковое направление и их длины равны. Этот пример даёт нам подсказку, как определить равенство векторов.
Но, прежде чем перейти к определению равенства векторов, введем несколько понятий, т. е. рассмотрим виды векторов.
Ненулевые векторы называются коллинеарными, если они лежат на одной прямой, либо на параллельных прямых. Нулевой вектор считается коллинеарным любому вектору. Если два вектора и коллинеарны, то это записывается так: || .
Если ненулевые коллинеарные векторы имеют одинаковое направление, то такие векторы будут сонаправленными. Если их направления противоположны, они называются противоположно направленными.
Для обозначения сонаправленных и противоположно направленных векторов существуют специальные обозначения: , если векторы и сонаправлены; , если векторы и противоположно направлены.
Что же с нулевым вектором? Его начало совпадает с концом. Поэтому он не имеет какого-то определённого направления. Другими словами, любое направление можно считать направлением нулевого вектора. А это значит, что нулевой вектор сонаправлен с любым вектором.
Ненулевые коллинеарные векторы обладают следующими свойствами:
Если , то
Если , то
Если , то
Пример 3
На рисунке 8 изображены векторы. Определите, какие векторы являются коллинеарными, какие не коллинеарными, сонаправленными и противоположно направленными.
Решение
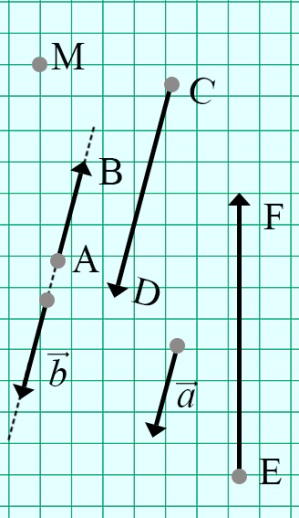 Рис. 8. Виды векторов
Рис. 8. Виды векторов
1. Определим, какие векторы коллинеарные и неколлинеарные.
Векторы .
Также , т.к. нулевой вектор коллинеарен любому вектору.
А векторы и , и , и , и неколлинеарные.
2. Определим сонаправленные векторы:
1) Вектор сонаправлен с любым из векторов.
2)
3. Определим противоположно направленные векторы:
Векторы называют равными, если они сонаправлены и их длины равны.
Пример 4
Начертить векторы и так, чтобы и были коллинеарны, а векторы и были не коллинеарны и длины векторов и были соответственно равны 7 см, 5 см и 3 см.
Решение
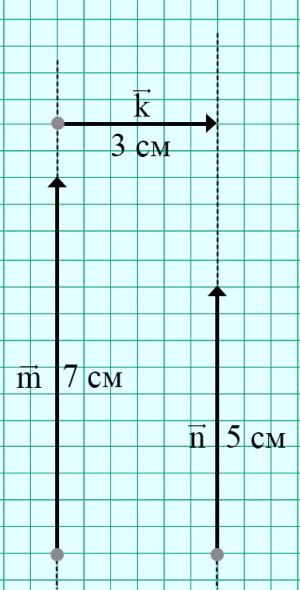 Рис. 9. Решение примера 4
Рис. 9. Решение примера 4
Чтобы векторы и были коллинеарны, они должны лежать, например, на параллельных прямых. Причём длина вектора равна 7 см, а длина вектора – 5 см.
Вектор изобразим так, чтобы он был не коллинеарным с вектором , а длина его была равна 3 см (Рис. 9).
Откладывание вектора от данной точки
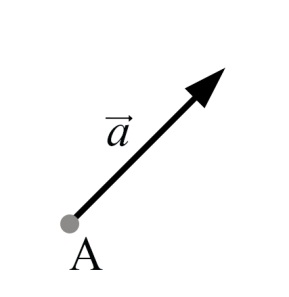 Рис. 10. Вектор отложен от точки
Рис. 10. Вектор отложен от точки
Если точка А является началом вектора , то говорят, что вектор отложен от точки А (Рис.10).
Утверждение:
От любой точки К можно отложить вектор, равный данному вектору , и притом только один.
Доказательство
1. Если – нулевой вектор, то = .
2. Если вектор ненулевой, точка A – начало этого вектора, а точка B – конец.
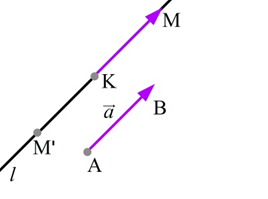 Рис. 11. Чертёж к доказательству
Рис. 11. Чертёж к доказательству
Проведём через точку K прямую l, параллельную AB.
На построенной прямой отложим отрезки KM и KM’, равные отрезку AB.
Выберем из векторов и вектор, который сонаправлен с вектором . На нашем чертеже (Рис. 11) это вектор .
Этот вектор будет равен вектору .
Из построения следует, что такой вектор единственный.
Упражнение 1
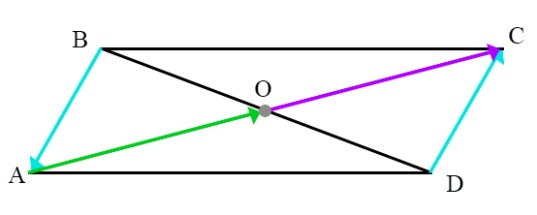 Рис. 12. Параллелограмм
Рис. 12. Параллелограмм
1. Перечислите все векторы, которые изображены на рисунке 12 (ABCD – параллелограмм). Укажите среди них: коллинеарные, сонаправленные, противоположно направленные и равные, используя обозначения.
 MNK" loading="lazy" />
Рис. 13. Треугольник MNK
MNK" loading="lazy" />
Рис. 13. Треугольник MNK
2. В треугольнике MNK стороны MN, NK и KM равны 8 см, 5 см и 10 см соответственно.
Точки P, O и L - середины сторон треугольника (Рис. 13).
Найти длины векторов
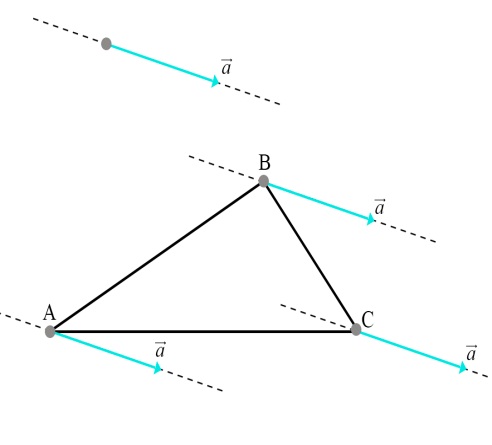
3. Отложите от вершин треугольника ABC векторы равные ненулевому вектору .
Контрольные вопросы
1. Дайте определение вектора.
2. Как обозначаются векторы?
3. Что значит нулевой вектор? Как обозначается?
4. Какие векторы называются коллинеарными? Как обозначаются?
5. Какие векторы являются сонаправленными, противоположно направленными? Как обозначаются?
6. Какое направление имеет нулевой вектор?
7. Какими свойствами обладают ненулевые коллинеарные векторы?
8. Что называется длиной (модулем) ненулевого вектора?
9. Сформулируйте определение равных векторов.
10. Объясните смысл выражения: «Вектор отложен от точки А».
1. Изображены векторы
2. 8 см; 5 см; 10 см; 4 см; 2,5 см; 5 см.
3.
- Понятие вектора
- Равенство векторов
- Откладывание вектора от данной точки
- Знать определения вектора, нулевого вектора, длины вектора, коллинеарных векторов, сонаправленных векторов, противоположно направленных и равных векторов
- Знать, как обозначаются коллинеарные векторы, сонаправленные и противоположно направленные векторы, длина вектора
- Уметь изображать и обозначать векторы, откладывать от данной точки вектор, равный данному.
- Установите, какие из величин характеризуются числовым значением, а какие и числовым значением, и направлением.
- температура
- масса
- скорость
- длина
- сила
- перемещение
Понятие вектора
Из физики известно, что некоторые величины характеризуются не только числовым значением, но и направлением.
 Рис. 1. Движение велосипедистов
Рис. 1. Движение велосипедистов
Величины бывают скалярными или векторными.
Скалярными называют величины, имеющие численное значение, но не имеющие направления.
Например, количество каких-нибудь предметов, длина, плотность.
Векторными величинами, или векторами, называют величины, имеющие и численное значение, и направление.
Например, если сказано, что велосипедист движется со скоростью 40 километров в час (то есть дано численное значение скорости), то про его движение известно не всё, потому что неизвестно, куда, в каком направлении он двигается. Примеры векторных величин — скорость, сила, перемещение.
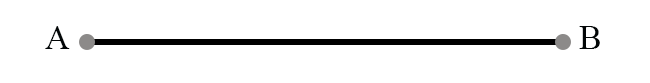 Рис. 2. Отрезок
Рис. 2. Отрезок
Рассмотрим произвольный отрезок АВ (Рис. 2). Точки А и В называют его концами или граничными точками.
 Рис. 3. Направленный отрезок
Рис. 3. Направленный отрезок
Итак, на данном отрезке можно указать два направления: от точки B к точке А и наоборот.
При выборе направления назовём одну граничную точку началом отрезка, в данном случае A, а другую — концом отрезка — B. Будем считать, что отрезок направлен от начала к концу (Рис. 3)
Отрезок, для которого указано, какая из его граничных точек считается началом, а какая — концом, называется направленным отрезком или вектором.
Вектор изображают в виде отрезка со стрелкой, показывающей направление вектора.
Вектор можно обозначить:
Двумя заглавными буквами, поставив над ними стрелочку; первая буква показывает начальную точку, вторая — конечную точку, например, − (читается: вектор AB);
Маленькой буквой со стрелочкой над ней, например, (читается: вектор a).
Если начальная и конечная точки вектора совпадают, получается нулевой вектор, который обозначается как . Любую точку на плоскости можно считать нулевым вектором.
Например, вектор, обозначенный точкой N, будет иметь название или .
Пример 1
Отметить точки M, N, K и P так, чтобы никакие 3 из них не лежали на одной прямой. Начертить все ненулевые векторы, начало и конец которых совпадают с какими-то двумя из этих точек. Выписать все полученные векторы и указать их начало и конец. Сколько векторов получилось?
Решение примера 1
 Рис. 4. Чертёж. Пример 1
Рис. 4. Чертёж. Пример 1
2. Составим таблицу, в которую будем записывать все полученные векторы, а также их начало и конец.
3. Построим искомые векторы.

Ответ: 12 векторов
 Рис. 5. Длина вектора
Рис. 5. Длина вектора
Можно говорить «модуль вектора АВ (модуль вектора а)».
При нахождении длины вектора мы не учитываем его направление.
Длина нулевого вектора равна 0:
Пример 2
 Рис. 6. Чертёж. Пример 2
Рис. 6. Чертёж. Пример 2
На рисунке 6 изображены векторы. Чему равна длина каждого вектора, если известно, что сторона клетки равна 1 см?
Решение
1. ||= || = 0 (см)
2. | | = CD = 3 (см)
3. || = FE = 7 (см)
4. || = AB = 9 (см)
5. || = ST = 5 (см)
Ответ: || = 0 см, || = 3 см, || = 7 см, || = 9 см, || = 5 см.
Равенство векторов
 Рис. 7. Движение в тандеме
Рис. 7. Движение в тандеме
(рис.7). Каждый из них движется в одном и том же направлении и с одной и той же скоростью. Скорость каждого спортсмена является векторной величиной, соответственно, изобразим её в виде вектора. Получим, что все направленные отрезки, изображающие скорости разных точек, имеют одинаковое направление и их длины равны. Этот пример даёт нам подсказку, как определить равенство векторов.
Но, прежде чем перейти к определению равенства векторов, введем несколько понятий, т. е. рассмотрим виды векторов.
Ненулевые векторы называются коллинеарными, если они лежат на одной прямой, либо на параллельных прямых. Нулевой вектор считается коллинеарным любому вектору. Если два вектора и коллинеарны, то это записывается так: || .
Если ненулевые коллинеарные векторы имеют одинаковое направление, то такие векторы будут сонаправленными. Если их направления противоположны, они называются противоположно направленными.
Для обозначения сонаправленных и противоположно направленных векторов существуют специальные обозначения: , если векторы и сонаправлены; , если векторы и противоположно направлены.
Что же с нулевым вектором? Его начало совпадает с концом. Поэтому он не имеет какого-то определённого направления. Другими словами, любое направление можно считать направлением нулевого вектора. А это значит, что нулевой вектор сонаправлен с любым вектором.
Ненулевые коллинеарные векторы обладают следующими свойствами:
Если , то
Если , то
Если , то
Пример 3
На рисунке 8 изображены векторы. Определите, какие векторы являются коллинеарными, какие не коллинеарными, сонаправленными и противоположно направленными.
Решение
 Рис. 8. Виды векторов
Рис. 8. Виды векторов
1. Определим, какие векторы коллинеарные и неколлинеарные.
Векторы .
Также , т.к. нулевой вектор коллинеарен любому вектору.
А векторы и , и , и , и неколлинеарные.
2. Определим сонаправленные векторы:
1) Вектор сонаправлен с любым из векторов.
2)
3. Определим противоположно направленные векторы:
Векторы называют равными, если они сонаправлены и их длины равны.
Пример 4
Начертить векторы и так, чтобы и были коллинеарны, а векторы и были не коллинеарны и длины векторов и были соответственно равны 7 см, 5 см и 3 см.
Решение
 Рис. 9. Решение примера 4
Рис. 9. Решение примера 4
Чтобы векторы и были коллинеарны, они должны лежать, например, на параллельных прямых. Причём длина вектора равна 7 см, а длина вектора – 5 см.
Вектор изобразим так, чтобы он был не коллинеарным с вектором , а длина его была равна 3 см (Рис. 9).
Откладывание вектора от данной точки
 Рис. 10. Вектор отложен от точки
Рис. 10. Вектор отложен от точки
Если точка А является началом вектора , то говорят, что вектор отложен от точки А (Рис.10).
Утверждение:
От любой точки К можно отложить вектор, равный данному вектору , и притом только один.
Доказательство
1. Если – нулевой вектор, то = .
2. Если вектор ненулевой, точка A – начало этого вектора, а точка B – конец.
 Рис. 11. Чертёж к доказательству
Рис. 11. Чертёж к доказательству
Проведём через точку K прямую l, параллельную AB.
На построенной прямой отложим отрезки KM и KM’, равные отрезку AB.
Выберем из векторов и вектор, который сонаправлен с вектором . На нашем чертеже (Рис. 11) это вектор .
Этот вектор будет равен вектору .
Из построения следует, что такой вектор единственный.
Упражнение 1
 Рис. 12. Параллелограмм
Рис. 12. Параллелограмм
1. Перечислите все векторы, которые изображены на рисунке 12 (ABCD – параллелограмм). Укажите среди них: коллинеарные, сонаправленные, противоположно направленные и равные, используя обозначения.
 MNK" loading="lazy" />
Рис. 13. Треугольник MNK
MNK" loading="lazy" />
Рис. 13. Треугольник MNK
2. В треугольнике MNK стороны MN, NK и KM равны 8 см, 5 см и 10 см соответственно.
Точки P, O и L - середины сторон треугольника (Рис. 13).
Найти длины векторов
3. Отложите от вершин треугольника ABC векторы равные ненулевому вектору .
Контрольные вопросы
1. Дайте определение вектора.
2. Как обозначаются векторы?
3. Что значит нулевой вектор? Как обозначается?
4. Какие векторы называются коллинеарными? Как обозначаются?
5. Какие векторы являются сонаправленными, противоположно направленными? Как обозначаются?
6. Какое направление имеет нулевой вектор?
7. Какими свойствами обладают ненулевые коллинеарные векторы?
8. Что называется длиной (модулем) ненулевого вектора?
9. Сформулируйте определение равных векторов.
10. Объясните смысл выражения: «Вектор отложен от точки А».
1. Изображены векторы
2. 8 см; 5 см; 10 см; 4 см; 2,5 см; 5 см.
3.


