Тест к уроку: Восточная Азия. Япония: «экономическое чудо»

Умножение вектора на число. Применение векторов к решению задач

План урока

Произведение вектора на число.
Применение векторов к решению задач
Средняя линия трапеции

Цели урока

Знать определение произведения вектора на число, свойства умножения вектора на число, правила действий с векторами, определение и свойство средней линии трапеции
Уметь применять свойства умножения вектора на число, применять векторы при доказательстве теорем и решении геометрических задач.

Разминка

В чём заключается правило многоугольника сложения нескольких векторов?
Какой вектор называется разностью двух векторов?
Какой вектор называется противоположным данному?
Что утверждает теорема о разности двух векторов?

Произведение вектора на число

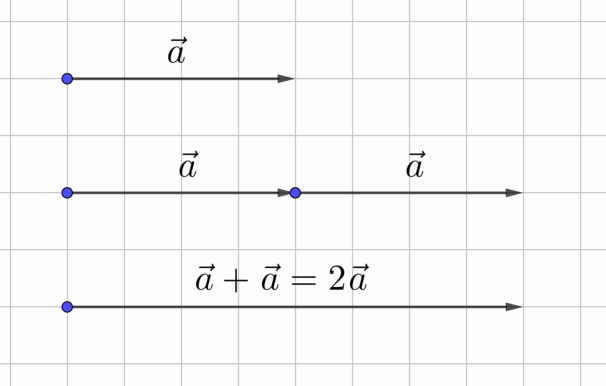Рис. 1.

Предположим, что нам надо сложить два равных вектора. В результате мы получим новый вектор, который будет сонаправлен с исходным, но его длина будет вдвое больше. Логично считать, что получившийся вектор вдвое больше исходного, то есть он получился при умножении вектора на число 2 (рис. 1).

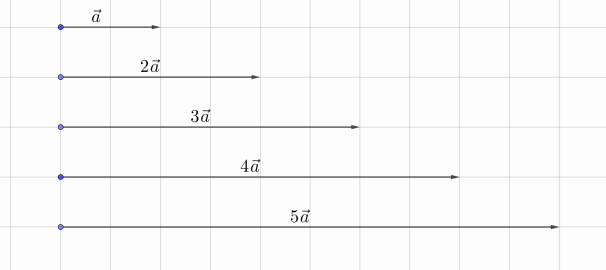Рис. 2. Умножение вектора на положительное число

Аналогично можно построить векторы, которые больше исходного не в 2, а в 3, 4 и т.д. раз (рис. 2). А как умножать вектор на отрицательное число?

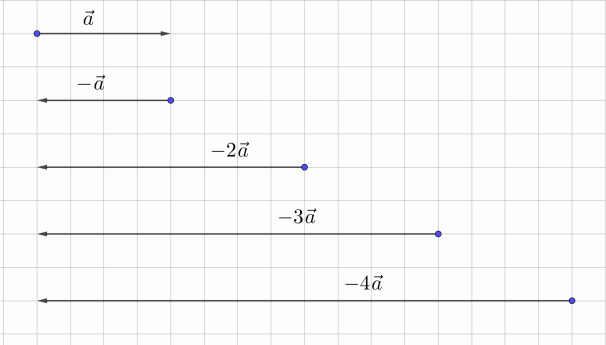Рис. 3. Умножение вектора на отрицательное число

Здесь нужно использовать противоположный вектор. Логично считать, что он получается при умножении (– 1) на вектор

(рис. 3). Данные примеры показывают, что удобно ввести операцию умножения вектора на число, и подсказывают, как дать соответствующее определение.

Произведением ненулевого вектора $\vec{a}$ на число $k$ называется такой вектор $\vec{b}$ , длина которого равна | $k$ |∙| $\vec{a}$ |, причем векторы $\vec{a}$ и $\vec{b}$ сонаправлены при $k \geq 0$ и противоположно направлены при $k < 0 .$

Из определения следует, что

Произведением нулевого вектора на любое число считается нулевой вектор.

Для любого числа $k$ и любого вектора $\vec{a}$ векторы $\vec{a}$ и $k \vec{a}$ коллинеарны.

Пример 1

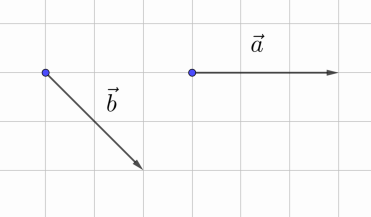Рис. 4. Пример 1

На рисунке 4 изображены два вектора. Найдите векторы $\vec{с} = 4 \vec{a} + 2 \vec{b}$ ,
$\vec{d} = 4 \vec{a} - 2 \vec{b}$

Решение

Рис. 5

1. Для построения

\vec{с}

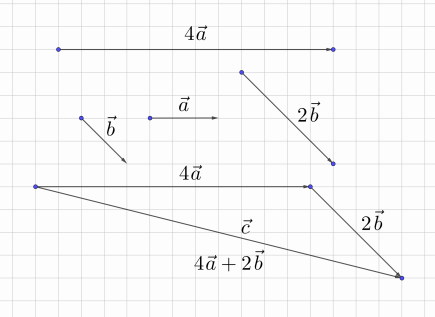нам надо сначала умножить исходные векторы на 4 и 2, а далее полученные результаты сложить по правилу треугольника (рис. 5).

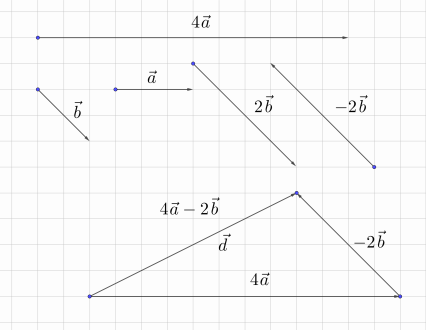Рис. 6

Для нахождения вектора $\vec{d}$ надо построить вектор, противоположный вектору $2 \vec{b}$ , и уже его складывать с $4 \vec{a}$ (рис. 6).

Умножение вектора на число обладает основными свойствами

Для любых чисел $k, l$ и любых векторов $\vec{a}, \vec{b}$ справедливы равенства:

1. $(k l) \vec{a} = k (l \vec{a})$ (сочетательный закон);

2. $(k + l) \vec{a} = k \vec{a} + l \vec{a}$ (первый распределительный закон);

3. $k (\vec{a} + \vec{b}) = k \vec{a} + k \vec{b}$ (второй распределительный закон).

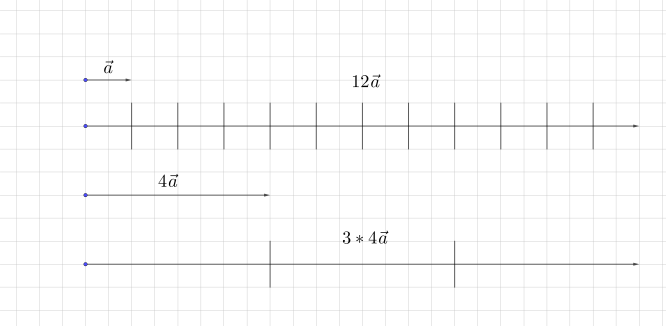Рис. 7. Сочетательный закон

Проиллюстрируем свойства на примерах:

Сочетательный закон (рис. 7). Рассмотрим вектор $12 \vec{a} = (3 \cdot 4) a ⃗ = 3 \cdot (4 \vec{a}) .$

Видно, что мы можем либо сразу умножить вектор $\vec{a}$ на число 12, либо сначала его умножить на 4, а потом на 3. Результат операции при этом не изменится

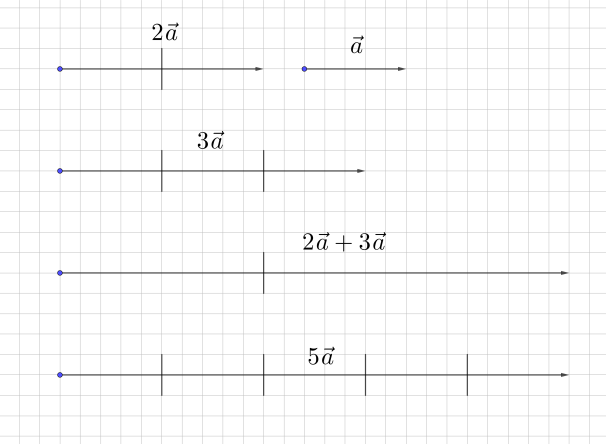Рис. 8. 1-ый распределительный закон

2. Первый распределительный закон (рис.8)

Необходимо сложить векторы 2 $\vec{a}$ и 3 $\vec{a}$ . Распределительный закон говорит, что мы можем поступить двумя способами. В первом случае мы просто строим векторы 2 $\vec{a}$ , 3 $\vec{a}$ и складываем их. Во втором случае мы складываем только числа 2 и 3 (получаем 5), и далее уже умножаем вектор $\vec{a}$ на число 5.

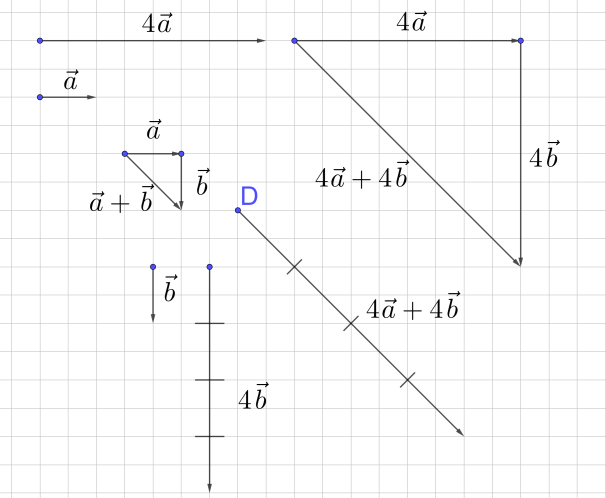Рис. 9. 2-ой распределительный закон

3. Второй распределительный закон (рис. 9), в котором в скобках находится уже сумма векторов, а не чисел. Необходимо, например, сложить векторы 4 $\vec{a}$ и 4 $\vec{b}$ . Конечно, можно просто построить их и сложить, однако закон говорит, что мы можем сначала сложить $\vec{a}$ и $\vec{b}$ , и уже потом эту сумму умножить на 4.

Сформулированные нами законы сложения и умножения векторов позволяют выполнять действия с векторами так же, как с числами. В том числе можно упрощать выражения, содержащие векторные величины. Например, пусть известны векторы $\vec{m}, \vec{n}$ и $\vec{k}$ , необходимо найти вектор

$\vec{p} = 2 (\vec{m} - \vec{n}) + (\vec{k} + \vec{m}) - 3 (\vec{n} - \vec{k} + \vec{m})$ .

Применим свойства: $\vec{p} = 2 \vec{m} - 2 \vec{n} + \vec{k} + \vec{m} - 3 \vec{n} + 3 \vec{k} - 3 \vec{m} = - 5 \vec{n} + 4 \vec{k} .$

Видно, что выражение значительно упростилось.

Применение векторов к решению задач

Векторы активно используются в физике при решении многих задач, однако они также помогают доказывать геометрические теоремы. Рассмотрим несколько примеров, и начнем со вспомогательной задачи.

Пример 2

Известно, что M – это середина отрезка EF. Докажите, что для любой точки O выполняется равенство: $\vec{О М} = \frac{1}{2} (\vec{О Е} + \vec{O F})$ .

Доказательство:

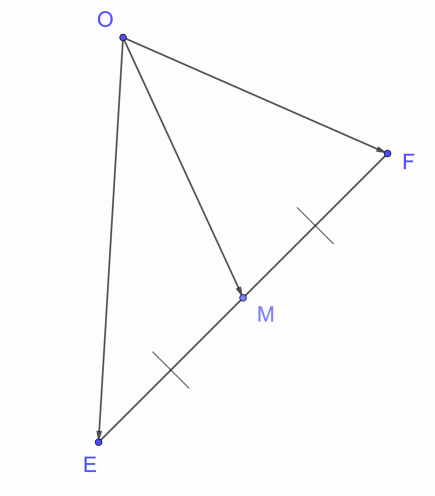Рис. 10

1. Используя правило треугольника, вектор $\vec{O M}$ можно представить в виде двух различных сумм:

$\vec{O M} = \vec{O E} + \vec{E M}, \vec{O M} = \vec{O F} + \vec{F M}$

2. Сложим правые и левые части этих равенств:

$2 \vec{O M} = \vec{O E} + \vec{O F} + \vec{E M} + \vec{F M} .$

3. Так как точка M – это середина отрезка EF, $\vec{E M}$ и $\vec{F M}$ - противоположные векторы, следовательно $\vec{E M} + \vec{F M} = \vec{0} .$

4. Значит, $2 \vec{O M} = \vec{O E} + \vec{O F}$ , $\vec{O M} = \frac{1}{2} (\vec{O E} + \vec{O F})$ .

Пример 3

Докажите, что если в трапеции провести прямую, проходящую через середины ее оснований, то она также пройдет через точку, в которой пересекаются продолжения боковых сторон трапеции.

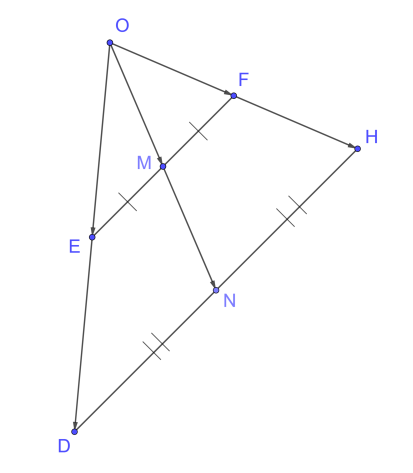Рис. 11. Пример 3

Доказательство

1. Построим трапецию DEFH, основаниями которой будут отрезки EF и DH. M и N – их середины соответственно. Прямые DE и FH пересекаются в точке O. Необходимо доказать, что прямая MN также проходит через О.

2. Заметим, что ∆ОFE и ∆ОHD подобны по двум углам. Действительно, у них есть общий угол DOH, а ∠ОFE = ∠OHD как соответственные углы при пересечении параллельных прямых секущей FH.

3. Обозначим коэффициент подобия буквой $k,$ тогда можно записать, что OD = $k$ ∙ OE,
OH = $k$ ∙ OF.

4. Так как $\vec{O D} ↑ ↑ \vec{O E}$ и $\vec{O H} ↑ ↑ \vec{O F}$ , то $\vec{O D} = k \cdot \vec{O E}$ , $\vec{O H} = k \cdot \vec{O F}$ .

5. M – это середина отрезка EF, поэтому $\vec{O M} = \frac{1}{2} \vec{(O E} + \vec{O F)}$ – см. доказательство Пример 2.

По аналогии $\vec{O N} = \frac{1}{2} (\vec{O D} + \vec{O H})$

6. Подставив в $\vec{O N} = \frac{1}{2} (\vec{O D} + \vec{O H})$ вместо $\vec{O D}$ и $\vec{O H}$ соответствующие равенства, получим $\vec{O N} = k \cdot \frac{1}{2} (\vec{O E} + \vec{O F}) = k \cdot \vec{O M}$ , следовательно $\vec{O N} ∥ \vec{O M}$ , N и M лежат на одной прямой (на параллельных прямых лежать не могут, т.к. имеют общую точку) и, значит, прямая MN проходит через О

Средняя линия трапеции

Отрезок, соединяющий середины боковых сторон трапеции, называется её средней линией.

Докажем теорему о средней линии трапеции, используя понятие вектора.

Теорема

Средняя линия трапеции параллельна основаниям и равна их полусумме.

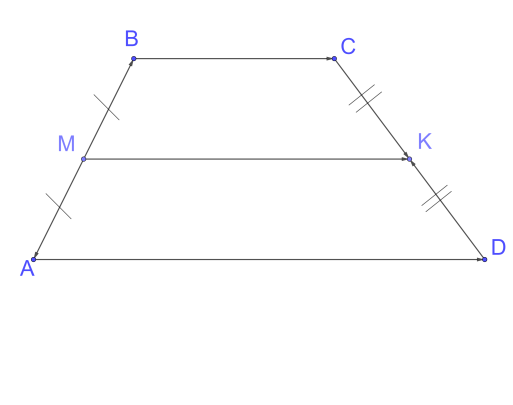Рис. 12. Чертёж. Теорема

Доказательство

1. Построим трапецию ABCD так, что отрезки AD и BC являются основаниями трапеции, а отрезки АВ и CD – боковыми сторонами. Проведем среднюю линию МК. Необходимо доказать: $М К ∥ A D$ , $M K = \frac{1}{2} (A D + B C) .$

2. Выразим вектор $\vec{M K}$ через сумму векторов по правилу многоугольника сначала одним, а затем другим способом.

$\vec{M K} = \vec{M B} + \vec{B C} + \vec{C K}$ , $\vec{M K} = \vec{M A} + \vec{A D} + \vec{D K}$ .

3. Сложим почленно два равенства и упростим получившееся выражение:

$2 \vec{M K} = \vec{(M B} + \vec{M A)} + (\vec{B C} + \vec{A D}) + \vec{(C K} + \vec{D K})$ ,

$2 \vec{M K} = \vec{0} + (\vec{B C} + \vec{A D}) + \vec{0} = \vec{B C} + \vec{A D}$ .

4. Выразим вектор $\vec{М К}$ через векторы $\vec{B C} и \vec{A D} : \vec{M K} = \frac{1}{2} (\vec{B C} + \vec{A D}), \vec{B C} ↑ ↑ \vec{A D}$ , тогда $\vec{M K} ↑ ↑ \vec{A D}$ , т.е. $M K ∥ A D$ .

5. Выразим длину вектора

$\vec{M K} : 2 | \vec{M K} | = | \vec{B C} + \vec{A D} | = | \vec{B C} | + | \vec{A D} | = \overset{}{В С} + \overset{}{A D}$ ,

значит $M K = \frac{1}{2} (В С + A D) .$

Следовательно, длина средней линии трапеции равна полусумме её оснований.

Упражнение 1

1. На рисунке 4 изображены два вектора. Найдите вектор $\vec{e} = - 4 \vec{a} + 2 \vec{b} .$

2. Дан произвольный треугольник MNK. Докажите, что существует треугольник, стороны которого соответственно параллельны и равны медианам треугольника MNK.

3. В равнобедренной трапеции MNKF перпендикуляр, опущенный из вершины N на большее основание MF, делит это основание на два отрезка, больший из которых равен 7 см. Найдите среднюю линию трапеции.

Контрольные вопросы

1. Какой вектор называется произведением данного вектора на число?

2. Чему равно произведение $k \vec{a}$ , если: $\vec{a} = \vec{0}$ , $k = 0$ ?

3. Могут ли векторы $\vec{a}$ и $k \vec{a}$ быть неколлинеарными?

4. Сформулируйте основные свойства умножения вектора на число.

5. Приведите пример применения векторов к решению задач.

6. Какой вектор называется разностью двух векторов? Постройте разность двух данных векторов.

7. Какой отрезок называется средней линией трапеции?

8. Сформулируйте и докажите теорему о средней линии трапеции.

Ответы

Упражнение 1

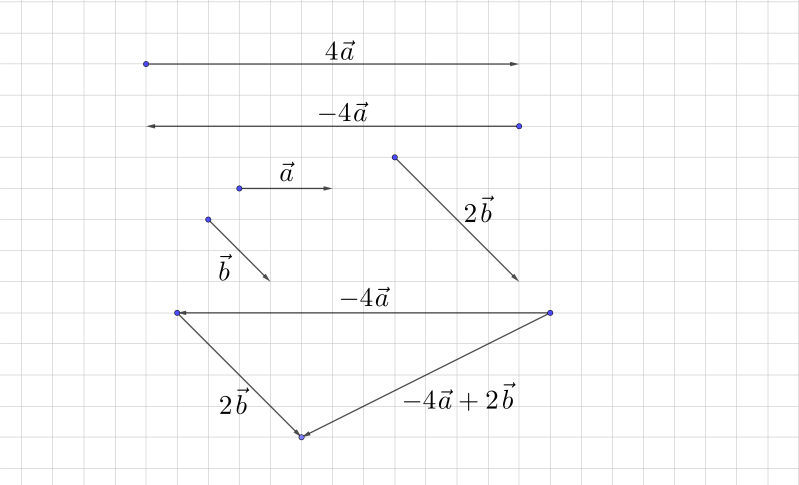1. Рис. 13

Рис. 13

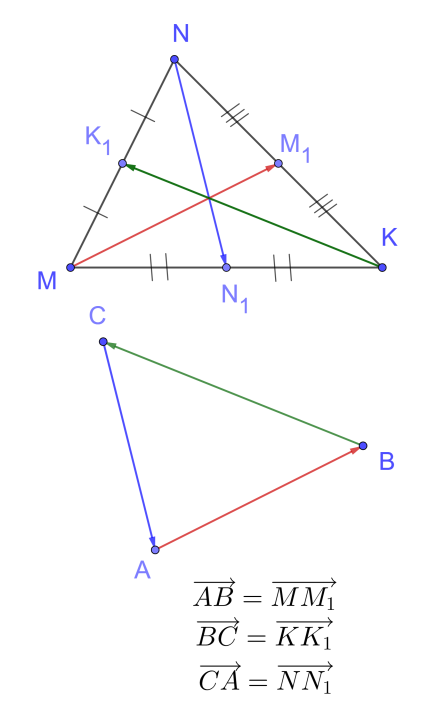2. Рис. 14

Рис. 14

3. 7 см

Конспект урока: Умножение вектора на число

Векторы на плоскости и в пространстве

Произведение вектора на число

Применение векторов к решению задач

Средняя линия трапеции