Уравнение окружности

План урока

Уравнение окружности
Взаимное расположение двух окружностей

Цели урока

Знать уравнение окружности данного радиуса с центром в данной точке в прямоугольной системе координат
Уметь выводить уравнение окружности, рассмотрев решение этой задачи как одну из возможностей применения метода координат
Уметь распознавать уравнение окружности по предложенному уравнению, составлять уравнение окружности по готовому чертежу, строить окружность по заданному уравнению
Знать все случаи взаимного расположения двух окружностей на плоскости
Знать в каком случае две окружности имеют одну общую точку, какие существуют виды касаний, когда две окружности пересекаются
Знать какие окружности называются концентрическими
Уметь определять взаимное расположение двух окружностей по их радиусам и расстоянию между центрами

Разминка

Какое уравнение называется уравнением данной линии?
Как найти длину dtrnjhf по его координатам?
Как вычислить расстояние между двумя точками по их координатам?
Что такое окружность, радиус окружности?

Уравнение окружности

Найдём по геометрическим свойствам линии ее уравнение. В качестве линии рассмотрим окружность. Сформулируем определение окружности:

Окружностью называется множество всех точек плоскости, равноудаленных от одной точки – от центра.

Рис. 1. Окружность (C; r)

Выведем уравнение окружности радиуса r с центром в точке C (рис. 1).

1. Пусть центр окружности имеет координаты (x₀; y₀).

2. Возьмем на окружности произвольную точку M (x; y).

3. Запишем формулу расстояния между точками C и M: $M C = \sqrt{{(x - x ₀)}^{2} + {(y - y ₀)}^{2}}$ ;

4. Мы знаем, что длина отрезка, который соединяет любую точку на окружности с центром окружности – это радиус.

Поэтому можно записать, что MC = r.

5. Возведем MC в квадрат и получим уравнение MC² = r².

6. Заменим MC² на выражение ${(x - x ₀)}^{2} + {(y - y ₀)}^{2}$

и получим, что если точка лежит на окружности радиуса r и с центром в точке с координатами $(x_{0}; y_{0})$ , то координаты этой точки удовлетворяют уравнению ${(x - x ₀)}^{2} + {(y - y ₀)}^{2} = r^{2}$

7. Если точка не лежит на окружности, например, K и N (рис. 1), то расстояние от этих точек до центра окружности не равно радиусу, поэтому координаты таких точек не будут удовлетворять полученному уравнению. Можно сказать, что

В прямоугольной системе координат уравнение окружности радиуса r с центром в точке C(x₀; y₀) имеет вид:

${(x - x ₀)}^{2} + {(y - y ₀)}^{2} = r^{2}$ .

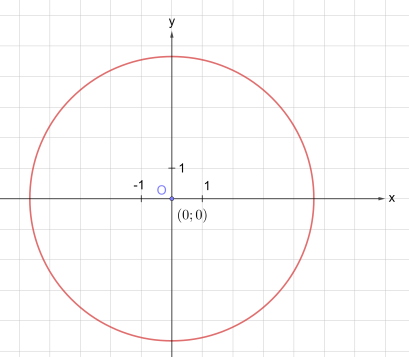Рис. 2. Окружность (O; r)

Запишем уравнение окружности радиуса r и с центром в начале координат (рис. 2).

Начало координат имеет координаты (0; 0). Подставим их в уравнение окружности ${(x - x ₀)}^{2} + {(y - y ₀)}^{2} = r^{2}$ и получим, что

Уравнение окружности радиуса r и с центром в начале координат имеет вид: x² + y² = r²

Пример 1

Постройте окружность, заданную уравнением

(x – 5)² + (y – 3)² = 4.

Решение

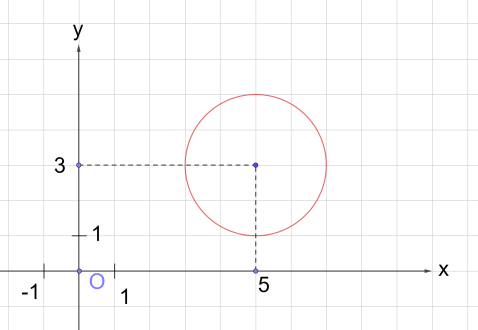Рис. 3

1. Запишем уравнение окружности в общем виде: ${(x - x ₀)}^{2} + {(y - y ₀)}^{2} = r^{2}$

2. Проанализируем исходное уравнение

(x – 5)² + (y – 3)² = 4.

Определимся с координатами центра окружности. Это будут числа 5 и 3, т.е. $(x_{0}; y_{0}) = (5; 3)$ .

Определим величину радиуса окружности. Поскольку в правой части формулы стоит квадрат радиуса, то для того, чтобы найти радиус надо извлечь квадратный корень из 4,

$r = \sqrt{4} = 2 .$

3. Значит, формула (x – 5)² + (y – 3)² = 4 задает окружность с центром в точке с координатами (5; 3) и радиусом, равным 2 (рис. 3).

Ответ: рис. 3.

Пример 2

Постройте окружность, заданную уравнением

x² + y² = 9

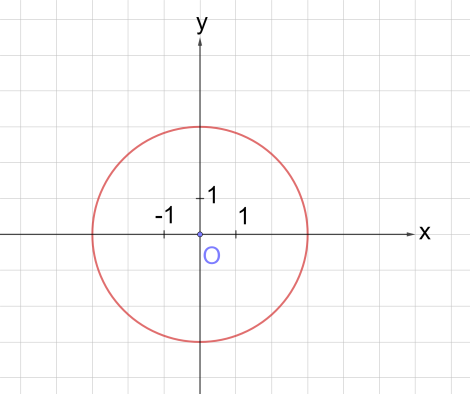Рис. 4

Решение

1. Уравнениями типа x² + y² = 9 описываются окружности с центром в начале координат.

2. Определим величину радиуса окружности. Поскольку в правой части формулы стоит квадрат радиуса, то для того, чтобы найти радиус надо извлечь квадратный корень из 9.

Таким образом, $r = \sqrt{9} = 3 .$

3. Значит, уравнение x² + y² = 9 задает окружность с центром в точке с координатами (0; 0) и радиусом, равным 3.

Ответ: рис. 4.

Пример 3

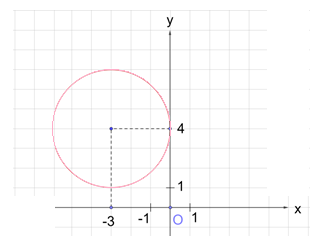Рис. 5

Составить уравнение окружности, которая показана на рисунке 5.

Решение

1. Найдём координаты (x₀; y₀) центра окружности: (-3; 4).

2. Определим радиус: r = 3.

3. Запишем общее уравнение окружности: ${(x - x ₀)}^{2} + {(y - y ₀)}^{2} = r^{2} .$

4. Подставим в уравнение найденные значения r, x₀, y₀:

(x + 3)² + (y – 4)² = 3².

(x + 3)² + (y – 4)² = 9 – искомое уравнение

Ответ: (x + 3)² + (y – 4)² = 9

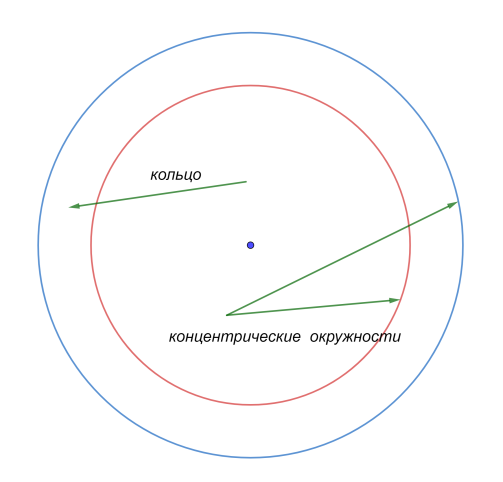Рис. 6. Кольцо и концентрические окружности

Взаимное расположение двух окружностей

Исследуем, как могут располагаться две окружности.

Для начала рассмотрим случай, когда центры окружностей совпадают
(рис. 6):

Если центры окружностей совпадают, то такие окружности называются концентрическими .

Если радиусы окружностей не равны, то такие окружности образуют кольцо .

Если радиусы окружностей равны, то окружности совпадают .

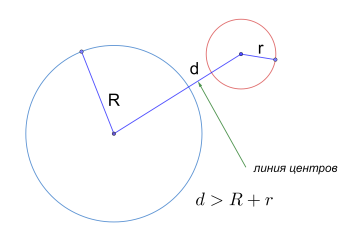Рис. 7. Окружности не пересекаются

Рассмотрим случаи, когда центры окружностей не совпадают. Соединим их, расстояние между ними обозначим d, и назовем линией центров данной пары окружностей (рис. 7).

В данном случае взаимное расположение окружностей будет зависеть от соотношения между величиной d и величинами радиусов окружностей.

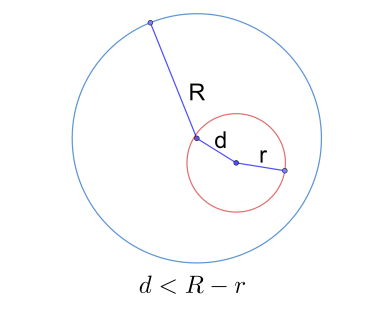Рис. 8. Окружности не пересекаются

Для того, чтобы было понятно, о какой окружности идет речь, радиус одной из окружностей обозначим за r, а радиус второй окружности – за R.

И будем считать, что r ≤ R.

Если d > R + r, то, очевидно, что окружности не пересекаются. В этом случае говорят, что одна окружность лежит вне другой (рис. 7).
Если d < R - r, то тогда одна окружность лежит внутри другой, но они не пересекаются (рис. 8).

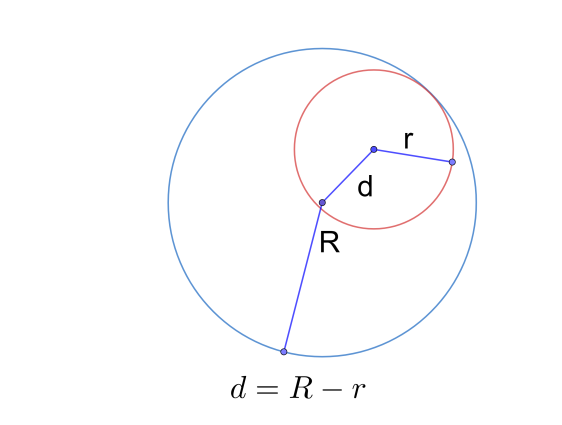Рис. 9. Внутренне касающиеся окружности

Если d = R - r, тогда малая окружность лежит внутри большой, но имеет с ней одну общую точку на линии центров. Такой случай называют внутренним касанием, а такие окружности называют внутренне касающимися (рис. 9)

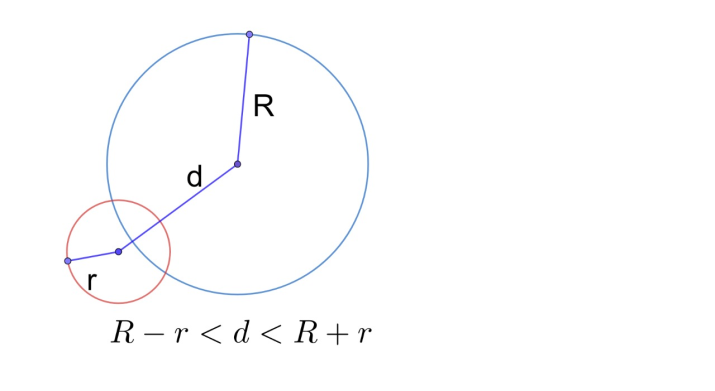Рис.10. Пересекающиеся окружности

Если R – r < d < R + r , то окружности пересекаются в двух точках и называются пересекающимися (рис. 10).

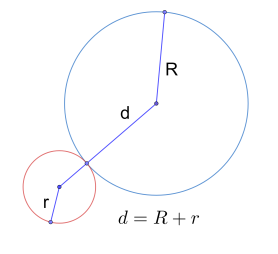Рис.11. Внешне касающиеся окружности

Если d = R + r, то такие окружности имеют одну общую точку, причем центр одной из них расположен за пределами второй окружности. Такой вид касания называется внешним касанием, а такие окружности называются внешне касающимися. Точка касания внешне касающихся окружностей лежит на линии центров (рис. 11).

Пример 4

Как располагаются окружности, если:

а) d = 15, R = 10, r = 5; б) d = 4, R = 8, r = 2

Решение

а) 15 = 10 + 5, значит d = R + r, таким образом, это внешне касающиеся окружности.

б) 4 < 8 – 2, значит, d < R - r, тогда одна окружность лежит внутри другой, но они не пересекаются.

Ответ: а) внешне касающиеся окружности; б) одна окружность лежит внутри другой, но они не пересекаются.

Пример 5

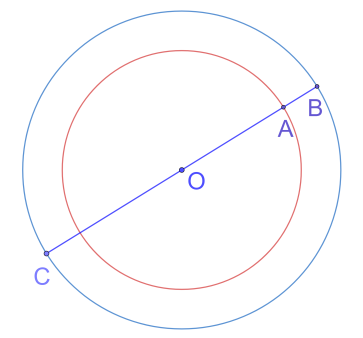Рис. 12. Пример 5

Наименьшее расстояние между точками двух концентрических окружностей равно 4 , а наибольшее равно 16. Найдите радиусы этих окружностей (рис. 12).

Решение

AB = 4;

AC = 16;

AC = AB + 2 ∙ OA;

2 ∙ OA = AC – AB;

2 ∙ OA = 12;

OA = 6;

OB = OA + AB;

OB = 6 + 4;

OB = 10.

Ответ: r = 6; R = 10.

Упражнение 1

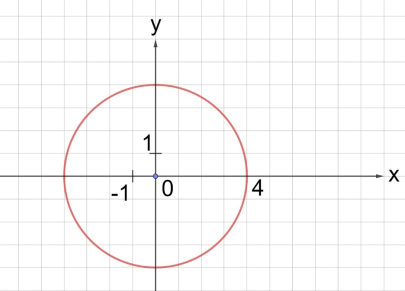Рис. 13. Упражнение 1.2

1. Написать уравнение окружности с диаметром MN, если N (2; 3), M (6; 3).

2. Составить уравнение окружности, которая показана на рисунке 13.

3. Как располагаются окружности, если:

а) d = 12, R = 6, r = 5; б) d = 7, R = 5,
r = 3

Контрольные вопросы

1. Выведите уравнение окружности данного радиуса с центром в данной точке.

2. Напишите уравнение окружности данного радиуса с центром в начале координат.

3. Как могут располагаться две окружности?

4. В каком случае окружности имеют одну общую точку?

5. Какие виды касаний вам известны?

6. Когда окружности пересекаются?

7. Какие окружности называются концентрическими?

Ответы

(x - 4)² + (y – 3)² = 4
x² + y² = 16

а) 12 > 6 + 5, окружности не пересекаются, одна окружность лежит вне другой;

б) 5-3 < 7 < 5+3, окружности пересекаются в двух точках (пересекающиеся окружности)

Конспект урока: Уравнение окружности

Окружность

Уравнение окружности

Взаимное расположение двух окружностей