- Длина окружности;
- Число Пи;
- Площадь круга;
- Площадь кругового сектора.
- Знать формулы длины окружности и длины дуги;
- Уметь применять формулы длины окружности и длины дуги для решения задач;
- Знать какое число обозначается буквой и чему равно его приближенное значение;
- Знать определения круга, кругового сектора и кругового сегмента;
- Знать формулы площади круга, площади кругового сектора и кругового сегмента;
- Уметь выводить формулы площади круга, площади кругового сектора и кругового сегмента, применять их при решении задач.
- Какой многоугольник называется правильным?
- Можно ли правильные многоугольники вписать в окружность?
- Можно ли описать окружность около правильного многоугольника?
- Чем круг отличается от окружности?
- Что такое дуга? Хорда?
Длина окружности
Для начала вспомним, что такое окружность.
Окружность – это геометрическое место точек, равноудаленных от данной точки. Эта точка называется центром окружности.
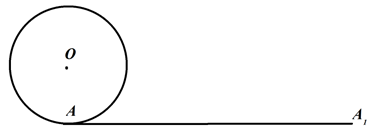 Рис. 1. Длина окружности
Рис. 1. Длина окружности
Чтобы получить наглядное представление о длине окружности, представим себе, что окружность сделана из нерастяжимой нити. Если разрезать эту нить в какой-нибудь точке и распрямить, то получится отрезок, длина которого будет равна длине окружности (рис.1).
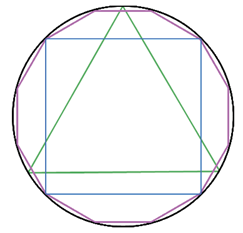 Рис. 2. Приближенное значение длины окружности
Рис. 2. Приближенное значение длины окружности
Если около правильного многоугольника описать окружность, то периметр этого многоугольника является приближенным значением длины окружности. Это приближенное значение длины окружности при увеличении числа сторон многоугольника становится практически равным периметру многоугольника (рис.2). Такое значение длины окружности - это предел, к которому стремится периметр правильного вписанного в окружность многоугольника при неограниченном увеличении числа его сторон.
Выведем формулу, выражающую длину окружности через её радиус.
Пусть и – длины окружностей радиусов и . В каждую из этих окружностей впишем правильный -угольник. Пусть и – периметры этих
-угольников, а и – их стороны. По формуле стороны правильного многоугольника , можно выразить периметр:
Тогда можно составить отношение
.
При любых значениях это равенство имеет место. Теперь будем неограниченно увеличивать значение . При , , тогда предел отношения равен . Но, с другой стороны, этот предел равен отношению . Таким образом, получаем:
.
Из этого равенства несложно получить:
.
В итоге мы показали, что отношение длины окружности к ее диаметру есть одно и то же число для всех окружностей. Это число принято обозначать как (читается «пи»).
Тогда из равенства получим формулу для вычисления длины окружности:
Длина окружности находится по формуле:
,
где - радиус окружности, - число, приближенно равное 3,14.
Длина дуги окружности находится по формуле:
,
где - радиус окружности, - число, приближенно равное 3,14, - градусная мера дуги окружности.
Докажем вторую формулу. Длина всей окружности равна , тогда длина дуги окружности, равной 1°, будет равна , Получили, что длина дуги с градусной мерой будет равна .
Пример 1
Найдите длину окружности, если её диаметр равен 10.
Решение
Сначала найдем радиус окружности как половину диаметра:
.
Вычислим длину окружности по формуле , приняв число :
Ответ: 31,4.
Упражнение 1
1. Найдите длину окружности, если её диаметр равен 18 ().
2. Найдите длину дуги окружности, если , градусная мера дуги ().
Число пи
Для всех окружностей отношение длины окружности к ее диаметру - это одно и то же число. Его принято обозначать греч. буквой (читается «пи»).
Это бесконечная непериодическая десятичная дробь.
Обозначение числа происходит от первой буквы греческих слов периферия, что означает «окружность» и периметр.
Рациональное число является приближенным значением числа с точностью до 0,002. Это приближенное значение было найдено ещё в III в. до н. э. великим греческим ученым Архимедом.
В XX в. с приходом компьютерных систем и вычислительной техники дело пошло быстрее: теперь уже точные десятичные значения высчитывали машины. С помощью специальных алгоритмов математики во всем мире продолжают определять новые, более точные значения числа пи, устанавливая рекорды по количеству цифр десятичного разложения (после запятой в десятичной дроби).
При решении задач обычно используют приближенное значение числа , равное 3,14.
Площадь круга
Круг – это часть плоскости, ограниченная окружностью.
Площадь круга равна квадрату радиуса, умноженному на отношение длины окружности к ее диаметру, т.е.
.
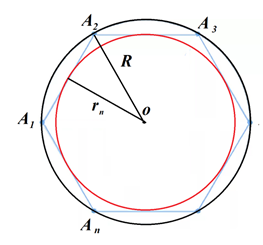 Рис. 3. Площадь круга
Рис. 3. Площадь круга
Докажем эту формулу. Пусть дан круг радиуса и с центром в точке (рис. 3).
Впишем в круг какой-нибудь правильный многоугольник . Легко заметить, что площадь круга будет больше площади правильного многоугольника , ведь многоугольник целиком лежит в круге. В многоугольник впишем круг радиуса с центром в точке . Его площадь будет меньше площади многоугольника , так как круг целиком лежит в многоугольнике. Таким образом, можно записать неравенство:
Представим себе, что число сторон правильного многоугольника неограниченно увеличивается, т.е. . По изученной ранее формуле: , где - радиус вписанной окружности, а - радиус описанной окружности. При значение , значит .
Мы получили, что при неограниченном увеличении сторон правильного многоугольника вписанная в него окружность «стремится» к описанной окружности, и тогда при .
Из формулы, где - периметр многоугольника , учитывая, что , , при , получим:
.
Задача
Построить с помощью циркуля и линейки квадрат, равновеликий данному кругу (равновеликие – имеющие одинаковую площадь).
Эта задача, известная под названием квадратуры круга, не может быть решена. Действительно, если обозначить буквой сторону искомого квадрата, а буквой радиус круга, то получим уравнение:
,
т.е. есть среднее пропорциональное между полуокружностью и радиусом. Значит, если известен отрезок, длина которого равна длине полуокружности, то легко построить квадрат, равновеликий данному кругу, и обратно: если известна сторона квадрата, равновеликого кругу, то можно построить отрезок, равный по длине полуокружности. Но с помощью циркуля и линейки нельзя построить отрезок, длина которого равнялась бы длине полуокружности; следовательно, нельзя в точности решить задачу о построении квадрата, равновеликого кругу. Приближенное решение можно выполнить, если предварительно найти приближенную длину полуокружности и затем построить среднее пропорциональное между отрезком этой длины и радиусом.
Пример 2
Найдите площадь круга, если его диаметр равен 12 .
Решение
Найдем радиус круга, как половину диаметра:
Вычислим площадь круга по формуле :
Ответ: 113,04.
Площадь кругового сектора
Круговым сектором (или просто сектором) называется часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга (рис. 4).
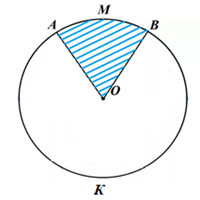 Рис. 4. Круговой сектор
Рис. 4. Круговой сектор
На рисунке 4 изображено два круговых сектора. Первый закрашенный сектор с дугой АМВ и второй сектор с дугой АКВ.
Площадь кругового сектора находится по формуле:
, где - радиус кругового сектора, - градусная мера дуги, ограничивающей сектор.
Действительно, так как площадь всего круга равна , то площадь сектора, ограниченного дугой в 1°, будет составлять . Поэтому площадь сектора, ограниченного дугой с градусной мерой будет составлять .
Круговым сегментом или просто сегментом называется часть круга, ограниченная дугой окружности и хордой, соединяющей концы этой дуги (рис. 5).
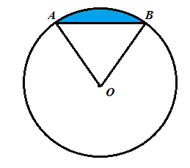 Рис. 5. Круговой сегмент
Рис. 5. Круговой сегмент
Очевидно, что если градусная мера дуги меньше 180°, то площадь сегмента легко найти, вычитая из площади сектора площадь равнобедренного треугольника, сторонами которого являются два радиуса и хорда сегмента.
Пример 3
Из круга, радиус которого равен 20 см, вырезан сектор с дугой в 90°. Чему равна площадь оставшейся части круга? .
Решение
Найдем площадь всего круга:
.
Найдем площадь сектора
.
Найдем площадь оставшейся части круга. Для этого из площади круга вычтем площадь сектора:
.
Ответ: 942 см2.
Упражнение 2
1. Найдите площадь круга, если его диаметр равен 24 ().
2. Из круга, радиус которого равен 30 см, вырезан сектор с дугой в 60°. Чему равна площадь оставшейся части круга ()?
Контрольные вопросы
1. Выведите формулу для вычисления длины окружности
2. Чему равно число ? Что оно означает?
3. Что такое круг?
4. Выведите формулу для вычисления площади круга
5. Что называется круговым сектором? Чему равна его площадь?
6. Что называется круговым сегментом? Чему равна его площадь?
Упражнение 1
1. 56,52.
2. 28,26
Упражнение 2
1. 452,16.
2. 2355 см2.
- Длина окружности;
- Число Пи;
- Площадь круга;
- Площадь кругового сектора.
- Знать формулы длины окружности и длины дуги;
- Уметь применять формулы длины окружности и длины дуги для решения задач;
- Знать какое число обозначается буквой и чему равно его приближенное значение;
- Знать определения круга, кругового сектора и кругового сегмента;
- Знать формулы площади круга, площади кругового сектора и кругового сегмента;
- Уметь выводить формулы площади круга, площади кругового сектора и кругового сегмента, применять их при решении задач.
- Какой многоугольник называется правильным?
- Можно ли правильные многоугольники вписать в окружность?
- Можно ли описать окружность около правильного многоугольника?
- Чем круг отличается от окружности?
- Что такое дуга? Хорда?
Длина окружности
Для начала вспомним, что такое окружность.
Окружность – это геометрическое место точек, равноудаленных от данной точки. Эта точка называется центром окружности.
 Рис. 1. Длина окружности
Рис. 1. Длина окружности
Чтобы получить наглядное представление о длине окружности, представим себе, что окружность сделана из нерастяжимой нити. Если разрезать эту нить в какой-нибудь точке и распрямить, то получится отрезок, длина которого будет равна длине окружности (рис.1).
 Рис. 2. Приближенное значение длины окружности
Рис. 2. Приближенное значение длины окружности
Если около правильного многоугольника описать окружность, то периметр этого многоугольника является приближенным значением длины окружности. Это приближенное значение длины окружности при увеличении числа сторон многоугольника становится практически равным периметру многоугольника (рис.2). Такое значение длины окружности - это предел, к которому стремится периметр правильного вписанного в окружность многоугольника при неограниченном увеличении числа его сторон.
Выведем формулу, выражающую длину окружности через её радиус.
Пусть и – длины окружностей радиусов и . В каждую из этих окружностей впишем правильный -угольник. Пусть и – периметры этих
-угольников, а и – их стороны. По формуле стороны правильного многоугольника , можно выразить периметр:
Тогда можно составить отношение
.
При любых значениях это равенство имеет место. Теперь будем неограниченно увеличивать значение . При , , тогда предел отношения равен . Но, с другой стороны, этот предел равен отношению . Таким образом, получаем:
.
Из этого равенства несложно получить:
.
В итоге мы показали, что отношение длины окружности к ее диаметру есть одно и то же число для всех окружностей. Это число принято обозначать как (читается «пи»).
Тогда из равенства получим формулу для вычисления длины окружности:
Длина окружности находится по формуле:
,
где - радиус окружности, - число, приближенно равное 3,14.
Длина дуги окружности находится по формуле:
,
где - радиус окружности, - число, приближенно равное 3,14, - градусная мера дуги окружности.
Докажем вторую формулу. Длина всей окружности равна , тогда длина дуги окружности, равной 1°, будет равна , Получили, что длина дуги с градусной мерой будет равна .
Пример 1
Найдите длину окружности, если её диаметр равен 10.
Решение
Сначала найдем радиус окружности как половину диаметра:
.
Вычислим длину окружности по формуле , приняв число :
Ответ: 31,4.
Упражнение 1
1. Найдите длину окружности, если её диаметр равен 18 ().
2. Найдите длину дуги окружности, если , градусная мера дуги ().
Число пи
Для всех окружностей отношение длины окружности к ее диаметру - это одно и то же число. Его принято обозначать греч. буквой (читается «пи»).
Это бесконечная непериодическая десятичная дробь.
Обозначение числа происходит от первой буквы греческих слов периферия, что означает «окружность» и периметр.
Рациональное число является приближенным значением числа с точностью до 0,002. Это приближенное значение было найдено ещё в III в. до н. э. великим греческим ученым Архимедом.
В XX в. с приходом компьютерных систем и вычислительной техники дело пошло быстрее: теперь уже точные десятичные значения высчитывали машины. С помощью специальных алгоритмов математики во всем мире продолжают определять новые, более точные значения числа пи, устанавливая рекорды по количеству цифр десятичного разложения (после запятой в десятичной дроби).
При решении задач обычно используют приближенное значение числа , равное 3,14.
Площадь круга
Круг – это часть плоскости, ограниченная окружностью.
Площадь круга равна квадрату радиуса, умноженному на отношение длины окружности к ее диаметру, т.е.
.
 Рис. 3. Площадь круга
Рис. 3. Площадь круга
Докажем эту формулу. Пусть дан круг радиуса и с центром в точке (рис. 3).
Впишем в круг какой-нибудь правильный многоугольник . Легко заметить, что площадь круга будет больше площади правильного многоугольника , ведь многоугольник целиком лежит в круге. В многоугольник впишем круг радиуса с центром в точке . Его площадь будет меньше площади многоугольника , так как круг целиком лежит в многоугольнике. Таким образом, можно записать неравенство:
Представим себе, что число сторон правильного многоугольника неограниченно увеличивается, т.е. . По изученной ранее формуле: , где - радиус вписанной окружности, а - радиус описанной окружности. При значение , значит .
Мы получили, что при неограниченном увеличении сторон правильного многоугольника вписанная в него окружность «стремится» к описанной окружности, и тогда при .
Из формулы, где - периметр многоугольника , учитывая, что , , при , получим:
.
Задача
Построить с помощью циркуля и линейки квадрат, равновеликий данному кругу (равновеликие – имеющие одинаковую площадь).
Эта задача, известная под названием квадратуры круга, не может быть решена. Действительно, если обозначить буквой сторону искомого квадрата, а буквой радиус круга, то получим уравнение:
,
т.е. есть среднее пропорциональное между полуокружностью и радиусом. Значит, если известен отрезок, длина которого равна длине полуокружности, то легко построить квадрат, равновеликий данному кругу, и обратно: если известна сторона квадрата, равновеликого кругу, то можно построить отрезок, равный по длине полуокружности. Но с помощью циркуля и линейки нельзя построить отрезок, длина которого равнялась бы длине полуокружности; следовательно, нельзя в точности решить задачу о построении квадрата, равновеликого кругу. Приближенное решение можно выполнить, если предварительно найти приближенную длину полуокружности и затем построить среднее пропорциональное между отрезком этой длины и радиусом.
Пример 2
Найдите площадь круга, если его диаметр равен 12 .
Решение
Найдем радиус круга, как половину диаметра:
Вычислим площадь круга по формуле :
Ответ: 113,04.
Площадь кругового сектора
Круговым сектором (или просто сектором) называется часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга (рис. 4).
 Рис. 4. Круговой сектор
Рис. 4. Круговой сектор
На рисунке 4 изображено два круговых сектора. Первый закрашенный сектор с дугой АМВ и второй сектор с дугой АКВ.
Площадь кругового сектора находится по формуле:
, где - радиус кругового сектора, - градусная мера дуги, ограничивающей сектор.
Действительно, так как площадь всего круга равна , то площадь сектора, ограниченного дугой в 1°, будет составлять . Поэтому площадь сектора, ограниченного дугой с градусной мерой будет составлять .
Круговым сегментом или просто сегментом называется часть круга, ограниченная дугой окружности и хордой, соединяющей концы этой дуги (рис. 5).
 Рис. 5. Круговой сегмент
Рис. 5. Круговой сегмент
Очевидно, что если градусная мера дуги меньше 180°, то площадь сегмента легко найти, вычитая из площади сектора площадь равнобедренного треугольника, сторонами которого являются два радиуса и хорда сегмента.
Пример 3
Из круга, радиус которого равен 20 см, вырезан сектор с дугой в 90°. Чему равна площадь оставшейся части круга? .
Решение
Найдем площадь всего круга:
.
Найдем площадь сектора
.
Найдем площадь оставшейся части круга. Для этого из площади круга вычтем площадь сектора:
.
Ответ: 942 см2.
Упражнение 2
1. Найдите площадь круга, если его диаметр равен 24 ().
2. Из круга, радиус которого равен 30 см, вырезан сектор с дугой в 60°. Чему равна площадь оставшейся части круга ()?
Контрольные вопросы
1. Выведите формулу для вычисления длины окружности
2. Чему равно число ? Что оно означает?
3. Что такое круг?
4. Выведите формулу для вычисления площади круга
5. Что называется круговым сектором? Чему равна его площадь?
6. Что называется круговым сегментом? Чему равна его площадь?
Упражнение 1
1. 56,52.
2. 28,26
Упражнение 2
1. 452,16.
2. 2355 см2.



