- Координаты середины отрезка;
- Вычисление длины вектора по его координатам;
- Расстояние между двумя точками.
- Уметь находить координаты середины отрезка;
- Знать формулу длины вектора по его координатам;
- Уметь находить длину вектора по его координатам;
- Знать формулу расстояния между точками;
- Уметь находить расстояние между двумя точками.
- Что такое вектор?
- Как найти координаты вектора в пространстве?
- Что означает запись ?
Координаты середины отрезка
В курсе планиметрии вы уже рассматривали подобные задачи.
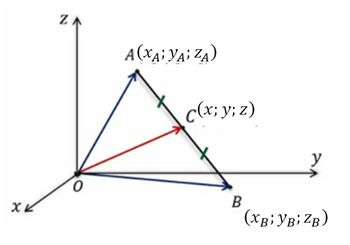 Рис. 1. Координаты середины отрезка
Рис. 1. Координаты середины отрезка
Обратимся к рисунку 1.
В прямоугольной системе координат отмечены три точки , и , причём - середина отрезка .
Построим три радиус-вектора: , и .
Из курса планиметрии известно, что если - середина отрезка , то
.
Пусть и . Координаты радиус-векторов и равны координатам этих точек соответственно, т.е. и . Тогда можем выразить координаты вектора
Получили, что . Так как координаты радиус-вектора совпадают с координатами точки то
.
Каждая координата середины отрезка равна полусумме соответствующих координат его концов.
Пример 1
Точка - середина отрезка . Найти координаты точки если и .
Решение
Так как - середина отрезка , то каждая её координата равна полусумме соответствующих координат его концов, т.е.
.
Выразим координаты точки :
.
Подставим координаты точек и :
.
Получили
.
Ответ: .
Упражнение 1
1. Найти координаты точки , если - середина отрезка и координаты концов равны:
а) и ;
б) и .
2. Точка - середина отрезка . Найти координаты точки если
а) и ;
б) и .
Вычисление длины вектора по его координатам
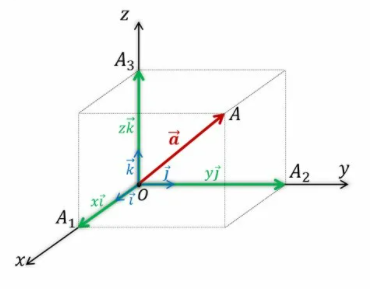 Рис. 2. Длина вектора по координатам
Рис. 2. Длина вектора по координатам
В прямоугольной системе координат (рис. 2) отмечена точка . Построим радиус-вектор . Если точка имеет координаты то вектор можно представить в виде
,
где , и .
Таким образом, имеем, что вектор является диагональю прямоугольного параллелепипеда, построенного на векторах , и , т.е.
.
Так как , и , то
.
Длина вектора вычисляется по формуле:
.
Для получения этой формулы, мы воспользовались свойством диагонали прямоугольного параллелепипеда, т.е. рассмотрели случай, когда точка не лежит на координатных плоскостях. Если бы точка лежала в одной из координатных плоскостей, то одна из её координат равнялась бы нулю (если она лежит на координатной прямой – две координаты равны нулю). Значит, формула верна для любого вектора в пространстве.
Пример 2
Длина вектора равна 7. Найти если .
Решение
Формула длины вектора имеет вид:
.
Подставим данные из условия:
,
отсюда
,
.
Так как , то .
Ответ: 6.
Упражнение 2
1. Найти длину вектора если
а) ; б) .
2. Длина вектора равна 3. Найти .
3. Длина вектора равна 15. Найти .
Расстояние между двумя точками
Расстояние между двумя точками – это длина отрезка, соединяющего эти точки.
Зная координаты двух точек в пространстве, можно найти координаты вектора. Зная координаты вектора, можно найти его длину. А так как длина вектора равна длине отрезка между этими точками, то с помощью формулы длины вектора, можно найти расстояние между двумя точками.
Пусть точка имеет координаты , а точка – координаты . Тогда координаты вектора имеют вид . Можно вычислить длину этого вектора по формуле: .
Соответственно, если расстояние между точками и , то .
Расстояние между двумя точками и вычисляется по формуле
.
Пример 3
Найдите периметр треугольника если , и .
Решение
Периметр – это сумма длин всех сторон, т.е.
.
Длины сторон равны расстоянию между соответствующими точками. Найдем эти длины:
,
,
.
Тогда
.
Ответ: .
Упражнение 3
Найдите периметр треугольника если , и .
Уравнение сферы
 R с центром A (x0; y0; z0)" loading="lazy" />
Рис. 3. Сфера радиуса R с центром A (x0; y0; z0)
R с центром A (x0; y0; z0)" loading="lazy" />
Рис. 3. Сфера радиуса R с центром A (x0; y0; z0)
Также, как и окружность на плоскости, сфера имеет свое уравнение в пространстве.
Пусть точка — центр сферы с координатами (; ; ) в прямоугольной системе координат , а — радиус этой сферы (рис. 3).
Отметим точку на сфере.
С одной стороны, является радиусом сферы, так как этот отрезок соединяет центр сферы с её точкой.
С другой стороны, длину отрезка можно вычислить с помощью формулы расстояния между двумя точками. Тогда получим:
или
.
В прямоугольной системе координат уравнение сферы радиуса с центром имеет вид
.
Пример 4
Написать уравнение сферы с центром в точке и радиусом .
Решение
Подставим в уравнение сферы координаты центра и длину радиуса:
,
.
Ответ: .
Упражнение 4
1. Напишите уравнение сферы с центром в точке и радиусом , если
а) , ; б) , .
2. Определите координаты центра и радиус, если уравнение сферы имеет вид:
а) ; б) .
Контрольные вопросы
1. Как найти координаты середины отрезка, если известны координаты его концов?
2. Как найти длину вектора в пространстве, если известны его координаты?
3. Почему формулы длины вектора по координатам и расстояния между двумя точками имеет один вид?
Упражнение 1
1.а) (0; 4; -1); б) (1,5; 0; -1,5);
2. а) (1; 2; 13); б) (10; -2; 11).
Упражнение 2
1 a) ; б) .
2. -2.
3. .
Упражнение 3
Упражнение 4
1. а) ;
б) .
2. а) , ;
б) , .
- Координаты середины отрезка;
- Вычисление длины вектора по его координатам;
- Расстояние между двумя точками.
- Уметь находить координаты середины отрезка;
- Знать формулу длины вектора по его координатам;
- Уметь находить длину вектора по его координатам;
- Знать формулу расстояния между точками;
- Уметь находить расстояние между двумя точками.
- Что такое вектор?
- Как найти координаты вектора в пространстве?
- Что означает запись ?
Координаты середины отрезка
В курсе планиметрии вы уже рассматривали подобные задачи.
 Рис. 1. Координаты середины отрезка
Рис. 1. Координаты середины отрезка
Обратимся к рисунку 1.
В прямоугольной системе координат отмечены три точки , и , причём - середина отрезка .
Построим три радиус-вектора: , и .
Из курса планиметрии известно, что если - середина отрезка , то
.
Пусть и . Координаты радиус-векторов и равны координатам этих точек соответственно, т.е. и . Тогда можем выразить координаты вектора
Получили, что . Так как координаты радиус-вектора совпадают с координатами точки то
.
Каждая координата середины отрезка равна полусумме соответствующих координат его концов.
Пример 1
Точка - середина отрезка . Найти координаты точки если и .
Решение
Так как - середина отрезка , то каждая её координата равна полусумме соответствующих координат его концов, т.е.
.
Выразим координаты точки :
.
Подставим координаты точек и :
.
Получили
.
Ответ: .
Упражнение 1
1. Найти координаты точки , если - середина отрезка и координаты концов равны:
а) и ;
б) и .
2. Точка - середина отрезка . Найти координаты точки если
а) и ;
б) и .
Вычисление длины вектора по его координатам
 Рис. 2. Длина вектора по координатам
Рис. 2. Длина вектора по координатам
В прямоугольной системе координат (рис. 2) отмечена точка . Построим радиус-вектор . Если точка имеет координаты то вектор можно представить в виде
,
где , и .
Таким образом, имеем, что вектор является диагональю прямоугольного параллелепипеда, построенного на векторах , и , т.е.
.
Так как , и , то
.
Длина вектора вычисляется по формуле:
.
Для получения этой формулы, мы воспользовались свойством диагонали прямоугольного параллелепипеда, т.е. рассмотрели случай, когда точка не лежит на координатных плоскостях. Если бы точка лежала в одной из координатных плоскостей, то одна из её координат равнялась бы нулю (если она лежит на координатной прямой – две координаты равны нулю). Значит, формула верна для любого вектора в пространстве.
Пример 2
Длина вектора равна 7. Найти если .
Решение
Формула длины вектора имеет вид:
.
Подставим данные из условия:
,
отсюда
,
.
Так как , то .
Ответ: 6.
Упражнение 2
1. Найти длину вектора если
а) ; б) .
2. Длина вектора равна 3. Найти .
3. Длина вектора равна 15. Найти .
Расстояние между двумя точками
Расстояние между двумя точками – это длина отрезка, соединяющего эти точки.
Зная координаты двух точек в пространстве, можно найти координаты вектора. Зная координаты вектора, можно найти его длину. А так как длина вектора равна длине отрезка между этими точками, то с помощью формулы длины вектора, можно найти расстояние между двумя точками.
Пусть точка имеет координаты , а точка – координаты . Тогда координаты вектора имеют вид . Можно вычислить длину этого вектора по формуле: .
Соответственно, если расстояние между точками и , то .
Расстояние между двумя точками и вычисляется по формуле
.
Пример 3
Найдите периметр треугольника если , и .
Решение
Периметр – это сумма длин всех сторон, т.е.
.
Длины сторон равны расстоянию между соответствующими точками. Найдем эти длины:
,
,
.
Тогда
.
Ответ: .
Упражнение 3
Найдите периметр треугольника если , и .
Уравнение сферы
 R с центром A (x0; y0; z0)" loading="lazy" />
Рис. 3. Сфера радиуса R с центром A (x0; y0; z0)
R с центром A (x0; y0; z0)" loading="lazy" />
Рис. 3. Сфера радиуса R с центром A (x0; y0; z0)
Также, как и окружность на плоскости, сфера имеет свое уравнение в пространстве.
Пусть точка — центр сферы с координатами (; ; ) в прямоугольной системе координат , а — радиус этой сферы (рис. 3).
Отметим точку на сфере.
С одной стороны, является радиусом сферы, так как этот отрезок соединяет центр сферы с её точкой.
С другой стороны, длину отрезка можно вычислить с помощью формулы расстояния между двумя точками. Тогда получим:
или
.
В прямоугольной системе координат уравнение сферы радиуса с центром имеет вид
.
Пример 4
Написать уравнение сферы с центром в точке и радиусом .
Решение
Подставим в уравнение сферы координаты центра и длину радиуса:
,
.
Ответ: .
Упражнение 4
1. Напишите уравнение сферы с центром в точке и радиусом , если
а) , ; б) , .
2. Определите координаты центра и радиус, если уравнение сферы имеет вид:
а) ; б) .
Контрольные вопросы
1. Как найти координаты середины отрезка, если известны координаты его концов?
2. Как найти длину вектора в пространстве, если известны его координаты?
3. Почему формулы длины вектора по координатам и расстояния между двумя точками имеет один вид?
Упражнение 1
1.а) (0; 4; -1); б) (1,5; 0; -1,5);
2. а) (1; 2; 13); б) (10; -2; 11).
Упражнение 2
1 a) ; б) .
2. -2.
3. .
Упражнение 3
Упражнение 4
1. а) ;
б) .
2. а) , ;
б) , .
