- Уравнение поверхности;
- Уравнение плоскости;
- Расстояние от точки до плоскости.
- Знать, что называют уравнением поверхности;
- Уметь записывать уравнение плоскости;
- Уметь находить расстояние от точки до плоскости.
- Что такое нормальный вектор плоскости?
- Что называют расстоянием от точки до плоскости?
- Какое уравнение задает прямую на плоскости?
Уравнение поверхности
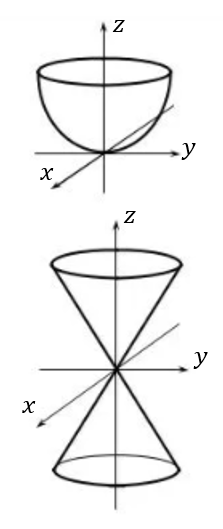 Рис. 1. Уравнения поверхности
Рис. 1. Уравнения поверхности
Если в пространстве задана прямоугольная система координат и дана некоторая поверхность то уравнение с тремя переменными называется уравнением поверхности , если этому уравнению удовлетворяют координаты любой точки поверхности и не удовлетворяют координаты никакой точки, не лежащей на этой поверхности.
На рисунке 1 изображены две поверхности и их уравнения:
1) ; 2) .
Уравнение плоскости
Вспомним, что нормальный вектор определяет плоскость. Нормальный вектор перпендикулярен плоскости, а значит и любой прямой, лежащей в этой плоскости.
Пусть плоскость проходит через точку и перпендикулярна вектору . Можем выбрать любую точку , принадлежащую плоскости . Тогда вектор и взаимно перпендикулярны, значит, их скалярное произведение равно нулю:
.
Если же точка не принадлежит плоскости, то векторы и не перпендикулярны и их скалярное произведение не равно нулю, т.е.
.
Мы вывели уравнение плоскости. Если раскрыть скобки, то можно получить уравнение в общем виде.
Уравнение является уравнением плоскости, проходящей через точку и перпендикулярной вектору .
Уравнение можно записать в виде , где .
Уравнение плоскости в прямоугольной системе координат является уравнением первой степени.
Пример 1
В единичном кубе напишите уравнение плоскости .
Решение
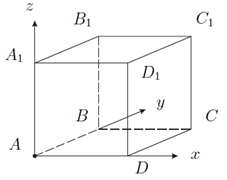 Рис. 2. Единичный куб
Рис. 2. Единичный куб
Введем систему координат с началом в точке (рис. 2)
Вектор перпендикулярен плоскости .
Определим координаты точки принадлежащей плоскости и точек :
.
Тогда координаты вектора .
Осталось подставить координаты вектора и точки в уравнение плоскости
,
,
.
Ответ: .
Упражнение 1
В единичном кубе напишите уравнение плоскости . Использовать систему координат из рисунка 2.
Расстояние от точки до плоскости
Рассмотрим плоскость , которая задана уравнением , и точку , лежащую вне этой плоскости.
Пусть точка – проекция на плоскость . Тогда координаты этой точки удовлетворяют уравнению плоскости , т.е.
.
Векторы и параллельны, так как перпендикулярны одной плоскости. Это значит, что , т.е.
.
Расстояние от точки до плоскости равно длине вектора , т.е.
.
Осталось выяснить чему равен коэффициент . Воспользуемся следующими полученными соотношениями:
;
.
Получим
,
.
Тогда
,
.
Пример 2
В единичном кубе найдите расстояние от точки пересечения диагоналей грани до плоскости .
Решение
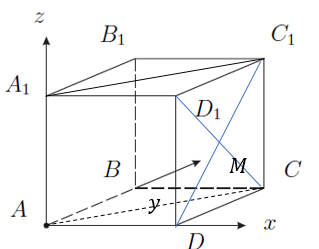 Рис. 3. Единичный куб
Рис. 3. Единичный куб
Введем систему координат с началом в точке (рис. 3).
Уравнение плоскости мы получили в примере 1:
.
Найдем координаты точки :
.
Подставим все в формулу расстояния:
,
.
Ответ: .
Упражнение 2
В единичном кубе найдите расстояние от точки пересечения диагоналей грани до плоскости .
Контрольные вопросы
1. Что такое уравнение поверхности?
2. Что нужно знать, чтобы записать уравнение плоскости?
3. Как найти расстояние от точки до плоскости методом координат?
Упражнение 1
.
Упражнение 2
.
- Уравнение поверхности;
- Уравнение плоскости;
- Расстояние от точки до плоскости.
- Знать, что называют уравнением поверхности;
- Уметь записывать уравнение плоскости;
- Уметь находить расстояние от точки до плоскости.
- Что такое нормальный вектор плоскости?
- Что называют расстоянием от точки до плоскости?
- Какое уравнение задает прямую на плоскости?
Уравнение поверхности
 Рис. 1. Уравнения поверхности
Рис. 1. Уравнения поверхности
Если в пространстве задана прямоугольная система координат и дана некоторая поверхность то уравнение с тремя переменными называется уравнением поверхности , если этому уравнению удовлетворяют координаты любой точки поверхности и не удовлетворяют координаты никакой точки, не лежащей на этой поверхности.
На рисунке 1 изображены две поверхности и их уравнения:
1) ; 2) .
Уравнение плоскости
Вспомним, что нормальный вектор определяет плоскость. Нормальный вектор перпендикулярен плоскости, а значит и любой прямой, лежащей в этой плоскости.
Пусть плоскость проходит через точку и перпендикулярна вектору . Можем выбрать любую точку , принадлежащую плоскости . Тогда вектор и взаимно перпендикулярны, значит, их скалярное произведение равно нулю:
.
Если же точка не принадлежит плоскости, то векторы и не перпендикулярны и их скалярное произведение не равно нулю, т.е.
.
Мы вывели уравнение плоскости. Если раскрыть скобки, то можно получить уравнение в общем виде.
Уравнение является уравнением плоскости, проходящей через точку и перпендикулярной вектору .
Уравнение можно записать в виде , где .
Уравнение плоскости в прямоугольной системе координат является уравнением первой степени.
Пример 1
В единичном кубе напишите уравнение плоскости .
Решение
 Рис. 2. Единичный куб
Рис. 2. Единичный куб
Введем систему координат с началом в точке (рис. 2)
Вектор перпендикулярен плоскости .
Определим координаты точки принадлежащей плоскости и точек :
.
Тогда координаты вектора .
Осталось подставить координаты вектора и точки в уравнение плоскости
,
,
.
Ответ: .
Упражнение 1
В единичном кубе напишите уравнение плоскости . Использовать систему координат из рисунка 2.
Расстояние от точки до плоскости
Рассмотрим плоскость , которая задана уравнением , и точку , лежащую вне этой плоскости.
Пусть точка – проекция на плоскость . Тогда координаты этой точки удовлетворяют уравнению плоскости , т.е.
.
Векторы и параллельны, так как перпендикулярны одной плоскости. Это значит, что , т.е.
.
Расстояние от точки до плоскости равно длине вектора , т.е.
.
Осталось выяснить чему равен коэффициент . Воспользуемся следующими полученными соотношениями:
;
.
Получим
,
.
Тогда
,
.
Пример 2
В единичном кубе найдите расстояние от точки пересечения диагоналей грани до плоскости .
Решение
 Рис. 3. Единичный куб
Рис. 3. Единичный куб
Введем систему координат с началом в точке (рис. 3).
Уравнение плоскости мы получили в примере 1:
.
Найдем координаты точки :
.
Подставим все в формулу расстояния:
,
.
Ответ: .
Упражнение 2
В единичном кубе найдите расстояние от точки пересечения диагоналей грани до плоскости .
Контрольные вопросы
1. Что такое уравнение поверхности?
2. Что нужно знать, чтобы записать уравнение плоскости?
3. Как найти расстояние от точки до плоскости методом координат?
Упражнение 1
.
Упражнение 2
.
