- Прямоугольная система координат в пространстве;
- Координаты вектора;
- Связь между координатами векторов и координатами точек.
- Знать, что представляет собой прямоугольная система координат в пространстве;
- Знать, что называют координатами вектора;
- Уметь выполнять сложение, вычитание векторов и умножение вектора на число в координатной форме;
- Уметь вычислять координаты вектора по координатам начала и конца вектора.
- Какие прямые называются перпендикулярными в пространстве?
- Что представляет собой прямоугольная система координат на плоскости?
- Что такое вектор?
Прямоугольная система координат в пространстве
Проведём три взаимно перпендикулярные прямые, пересекающиеся в одной точке O. Выберем единичный отрезок и направление для каждой из проведённых прямых. В результате получим прямоугольную систему координат.
Определение 1
Три взаимно перпендикулярные прямые, пересекающиеся в одной точке, с выбранными направлениями и единичным отрезком представляют собой прямоугольную систему координат в пространстве.
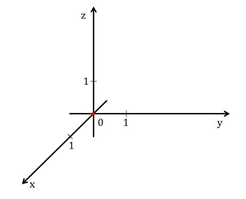 Рис. 1.
Рис. 1.
Точка пересечения осей называется началом координат и обозначается буквой . Координатные оси обозначаются , и и соответственно называются осью абсцисс, осью ординат и осью аппликат. Выбранное положительное направление на каждой оси указывается стрелкой (рис. 1).
Плоскости, проходящие через координатные оси и , и , и , называются координатными плоскостями и обозначаются соответственно , и .
Каждая из осей координат точкой делится на два луча. Луч, направление которого совпадает с направлением оси, называется положительной полуосью, другой – отрицательной полуосью.
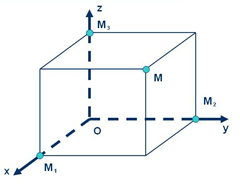 Рис. 2.
Рис. 2.
Если задана прямоугольная система координат, то каждой точке пространства соответствует некоторая тройка чисел (; ; ), которые называются координатами данной точки. Чтобы определить координаты точки (рис. 2), проведём через неё три плоскости, перпендикулярные к осям координат, и обозначим , , точки пересечения этих плоскостей соответственно с осями , , .
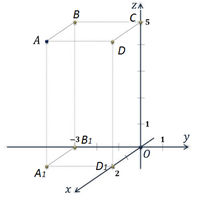 Рис. 3.
Рис. 3.
Координатой точки называют число, равное по абсолютной величине длине отрезка : положительное, если лежит на положительной полуоси , и отрицательное, если эта точка лежит на отрицательной полуоси. Аналогично определяются координаты и точки . Координаты точки при этом записываются следующим образом (; ; ).
Сначала записывает абсцисса, потом – ордината, и в последнюю очередь – аппликата.
Пользуясь этим правилом, запишем координаты точек, изображённых на рисунке 3:
,
.
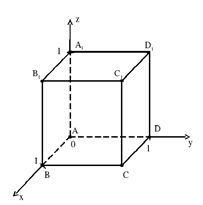 Рис. 4.
Рис. 4.
Упражнение 1
Запишите координаты вершин куба, изображённого на рисунке 4.
Координаты вектора
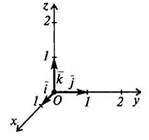 Рис. 5.
Рис. 5.
Рассмотрим в пространстве прямоугольную систему координат . На каждой из осей от начала координат в положительном направлении отложим вектор, длина которого равна единице (единичный вектор).
Введём следующие обозначения:
– единичный вектор оси абсцисс;
– единичный вектор оси ординат;
– единичный вектор оси аппликат.
Эти векторы называют координатными векторами (рис. 5).
Так как координатные векторы не компланарны, то любой вектор можно разложить по этим векторам, т.е. представить в виде
,
где , и – некоторые числа (коэффициенты разложения), определяемые единственным образом. Эти коэффициенты называются координатами вектора в данной системе координат и записывают .
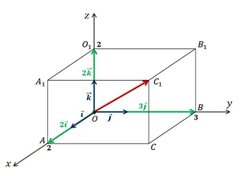 Рис. 6.
Рис. 6.
Пример 1
На рисунке 6 в прямоугольном параллелепипеде , , . Найдите координаты векторов , , , , , , , .
Решение
;
;
;
;
;
;
;
.
Рассмотрим правила, с помощью которых по координатам данных векторов можно найти координаты суммы и разности данных векторов, а также произведения данного вектора на данное число.
- Если , – данные векторы, то вектор имеет координаты или каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов.
- Если , – данные векторы, то вектор имеет координаты или каждая координата разности двух векторов равна разности соответствующих координат этих векторов.
- Если – данный вектор, – данное число, то вектор имеет координаты или каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.
Упражнение 2
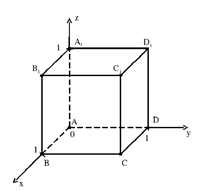 Рис. 7.
Рис. 7.
- На рисунке 7 изображён куб с ребром, равным 1. Запишите координаты векторов .
- Запишите координаты векторов: , , , , .
- Даны векторы и . Найдите координаты векторов:
а) ; б) ; в) ; г) ; д) .
Координаты точки и координаты вектора
Определение 2
Радиус-вектором данной точки называется вектор, начало которого совпадает с началом координат, а конец – с данной точкой.
Из определения следует, что координаты точки являются координатами и радиус-вектора этой точки, т.е.
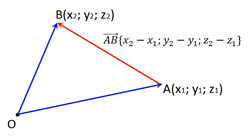 Рис. 8.
Рис. 8.
Рассмотрим теперь две произвольные точки и (рис. 8).
Вектор равен разности векторов и .
Выполним вычитание векторов в координатной форме
Таким образом, установили связь межу координатами вектора и координатами начала и конца этого вектора.
Каждая координата вектора равна разности соответствующих координат его конца и начала.
Упражнение 3
- Вычислите координаты векторов , и , если , , .
- Даны точки , , , . Докажите, что векторы и равны.
Контрольные вопросы
- Как определяются координаты точки в пространстве?
- Как определяются координаты вектора в пространстве?
- Как связаны координаты вектора с координатами его начала и конца?
Ответы
Упражнение 1
;
.
Упражнение 2
1. ;
.
2. ;
3. а) ; б) ; в) ;
г) д) .
Упражнение 3
.
- Прямоугольная система координат в пространстве;
- Координаты вектора;
- Связь между координатами векторов и координатами точек.
- Знать, что представляет собой прямоугольная система координат в пространстве;
- Знать, что называют координатами вектора;
- Уметь выполнять сложение, вычитание векторов и умножение вектора на число в координатной форме;
- Уметь вычислять координаты вектора по координатам начала и конца вектора.
- Какие прямые называются перпендикулярными в пространстве?
- Что представляет собой прямоугольная система координат на плоскости?
- Что такое вектор?
Прямоугольная система координат в пространстве
Проведём три взаимно перпендикулярные прямые, пересекающиеся в одной точке O. Выберем единичный отрезок и направление для каждой из проведённых прямых. В результате получим прямоугольную систему координат.
Определение 1
Три взаимно перпендикулярные прямые, пересекающиеся в одной точке, с выбранными направлениями и единичным отрезком представляют собой прямоугольную систему координат в пространстве.
 Рис. 1.
Рис. 1.
Точка пересечения осей называется началом координат и обозначается буквой . Координатные оси обозначаются , и и соответственно называются осью абсцисс, осью ординат и осью аппликат. Выбранное положительное направление на каждой оси указывается стрелкой (рис. 1).
Плоскости, проходящие через координатные оси и , и , и , называются координатными плоскостями и обозначаются соответственно , и .
Каждая из осей координат точкой делится на два луча. Луч, направление которого совпадает с направлением оси, называется положительной полуосью, другой – отрицательной полуосью.
 Рис. 2.
Рис. 2.
Если задана прямоугольная система координат, то каждой точке пространства соответствует некоторая тройка чисел (; ; ), которые называются координатами данной точки. Чтобы определить координаты точки (рис. 2), проведём через неё три плоскости, перпендикулярные к осям координат, и обозначим , , точки пересечения этих плоскостей соответственно с осями , , .
 Рис. 3.
Рис. 3.
Координатой точки называют число, равное по абсолютной величине длине отрезка : положительное, если лежит на положительной полуоси , и отрицательное, если эта точка лежит на отрицательной полуоси. Аналогично определяются координаты и точки . Координаты точки при этом записываются следующим образом (; ; ).
Сначала записывает абсцисса, потом – ордината, и в последнюю очередь – аппликата.
Пользуясь этим правилом, запишем координаты точек, изображённых на рисунке 3:
,
.
 Рис. 4.
Рис. 4.
Упражнение 1
Запишите координаты вершин куба, изображённого на рисунке 4.
Координаты вектора
 Рис. 5.
Рис. 5.
Рассмотрим в пространстве прямоугольную систему координат . На каждой из осей от начала координат в положительном направлении отложим вектор, длина которого равна единице (единичный вектор).
Введём следующие обозначения:
– единичный вектор оси абсцисс;
– единичный вектор оси ординат;
– единичный вектор оси аппликат.
Эти векторы называют координатными векторами (рис. 5).
Так как координатные векторы не компланарны, то любой вектор можно разложить по этим векторам, т.е. представить в виде
,
где , и – некоторые числа (коэффициенты разложения), определяемые единственным образом. Эти коэффициенты называются координатами вектора в данной системе координат и записывают .
 Рис. 6.
Рис. 6.
Пример 1
На рисунке 6 в прямоугольном параллелепипеде , , . Найдите координаты векторов , , , , , , , .
Решение
;
;
;
;
;
;
;
.
Рассмотрим правила, с помощью которых по координатам данных векторов можно найти координаты суммы и разности данных векторов, а также произведения данного вектора на данное число.
- Если , – данные векторы, то вектор имеет координаты или каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов.
- Если , – данные векторы, то вектор имеет координаты или каждая координата разности двух векторов равна разности соответствующих координат этих векторов.
- Если – данный вектор, – данное число, то вектор имеет координаты или каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.
Упражнение 2
 Рис. 7.
Рис. 7.
- На рисунке 7 изображён куб с ребром, равным 1. Запишите координаты векторов .
- Запишите координаты векторов: , , , , .
- Даны векторы и . Найдите координаты векторов:
а) ; б) ; в) ; г) ; д) .
Координаты точки и координаты вектора
Определение 2
Радиус-вектором данной точки называется вектор, начало которого совпадает с началом координат, а конец – с данной точкой.
Из определения следует, что координаты точки являются координатами и радиус-вектора этой точки, т.е.
 Рис. 8.
Рис. 8.
Рассмотрим теперь две произвольные точки и (рис. 8).
Вектор равен разности векторов и .
Выполним вычитание векторов в координатной форме
Таким образом, установили связь межу координатами вектора и координатами начала и конца этого вектора.
Каждая координата вектора равна разности соответствующих координат его конца и начала.
Упражнение 3
- Вычислите координаты векторов , и , если , , .
- Даны точки , , , . Докажите, что векторы и равны.
Контрольные вопросы
- Как определяются координаты точки в пространстве?
- Как определяются координаты вектора в пространстве?
- Как связаны координаты вектора с координатами его начала и конца?
Ответы
Упражнение 1
;
.
Упражнение 2
1. ;
.
2. ;
3. а) ; б) ; в) ;
г) д) .
Упражнение 3
.


