Умножение дробей. Возведение дроби в степень

План урока

Правило умножения дробей
Применение правила умножения дробе
Правило возведения дроби в натуральную степень;
Применение правила возведения дроби в натуральную степень

Цели урока

Знать правило умножения дробей
Уметь выполнять преобразование в дробь произведение двух и более дробей (в том числе, если один из множителей многочлен)
Знать правило возведения дроби в натуральную степень
Уметь выполнять преобразования выражений, содержащих степень дроби

Разминка

Представьте в виде степени с основанием y:

а) $y \cdot y^{3}$ ; б) ${(y^{3})}^{5}$ ; в) ${(\frac{y^{3}}{y})}^{4}$ .

Выполните действия:

а) $\frac{5}{7} \cdot \frac{2}{3}$ ; б) $\frac{1}{4} \cdot \frac{12}{3}$ ; в) $\frac{1}{3} \cdot 2$ ; г) $\frac{5}{6} \cdot 18$ .

Правило умножения дробей

Умножение рациональных дробей выполняется по тому же правилу, что и умножение обыкновенных дробей:

$\frac{a}{b} \cdot \frac{c}{d} = \frac{a c}{b d}$ ,

где a, b, c, d — некоторые многочлены, причем b и d — ненулевые многочлены.

Чтобы умножить дробь на дробь, нужно перемножить их числители и перемножить их знаменатели и первое произведение записать числителем, а второе — знаменателем дроби.

Применение правила умножения дробей

Рассмотрим применение правила умножения дробей на конкретных примерах.

Пример 1

Выполните умножение дробей: $\frac{2 y}{9 x} \cdot \frac{3 x}{y^{2}}$ .

Решение

Воспользуемся правилом умножения дробей:

$\frac{2 y}{9 x} \cdot \frac{3 x}{y^{2}} = \frac{2 y \cdot 3 x}{9 x \cdot y^{2}} = \frac{6 x y}{9 x y^{2}} = \frac{2}{3 y}$ .

Ответ: $\frac{2}{3 y}$ .

Пример 2

Выполните умножение дробей: $\frac{x - y}{x^{2} + x y} \cdot \frac{y^{2} + x y}{(x - y)^{2}} .$

Решение

Разложим на множители знаменатель первой дроби и числитель второй дроби, воспользуемся правилом умножения дробей, и сократим полученную дробь:

$\frac{x - y}{x^{2} + x y} \cdot \frac{y^{2} + x y}{(x - y)^{2}} = \frac{(x - y) \cdot y (x + y)}{x (x + y) \cdot (x - y)^{2}} = \frac{y}{x (x - y)} = \frac{y}{x^{2} - x y}$ .

Ответ: $\frac{y}{x^{2} - x y}$ .

Пример 3

Представьте произведение $\frac{y + 2}{x - y} \cdot \frac{y}{x + y}$ в виде рациональной дроби.

Решение

$\frac{y + 2}{x - y} \cdot \frac{y}{x + y} = \frac{(y + 2) \cdot y}{(x - y) \cdot (x + y)} = \frac{y^{2} + 2 y}{x^{2} - y^{2}}$ .

Ответ: $\frac{y^{2} + 2 y}{x^{2} - y^{2}}$ .

Пример 4

Выполните действия: $\frac{x - 2}{x^{2} - 4 x + 4} \cdot (x^{2} - 4)$ .

Решение

При умножении дроби на многочлен этот многочлен записывают в виде дроби со знаменателем 1 и затем применяют правило умножения дробей:

$\frac{x - 2}{x^{2} - 4 x + 4} \cdot (x^{2} - 4) = \frac{x - 2}{(x - 2)^{2}} \cdot \frac{(x^{2} - 4)}{1} = \frac{1 \cdot (x - 2) (x + 2)}{(x - 2) \cdot 1} = x + 2$ .

Ответ: $x + 2$ .

Упражнение 1

Выполните действия с дробями:

а) $\frac{a^{2} b}{12 c} \cdot \frac{4 c}{a b^{2}}$ ; б) $6 x \cdot \frac{a}{3 x^{2}}$ ; в) $\frac{3}{x^{2} - 2 x} \cdot \frac{2 x - 4}{x}$ ; г) $(3 a - 6 b) \cdot \frac{a + 2 b}{a^{2} - 4 b^{2}}$ .

Правило умножения дробей можно распространить на случай произведения трёх и более рациональных дробей, сгруппировав множители попарно:

$\frac{a}{b} \cdot \frac{c}{d} \cdot \frac{k}{l} = (\frac{a}{b} \cdot \frac{c}{d}) \cdot \frac{k}{l} = \frac{a c}{b d} \cdot \frac{k}{l} = \frac{a c k}{b d l}$ .

Правило возведения дроби в степень

Докажем правило возведения рациональной дроби в степень. Воспользуемся определением степени числа:

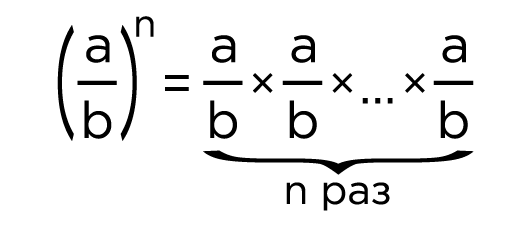
Применим правило умножения дробей в случае нескольких множителей:

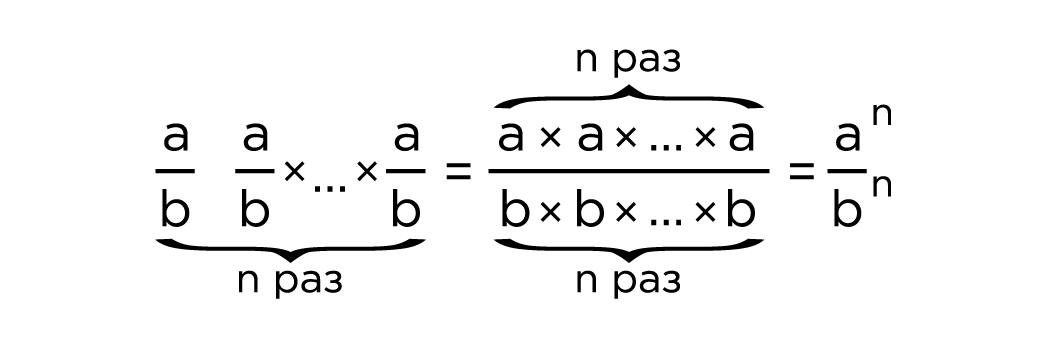
Таким образом, ${(\frac{a}{b})}^{n} = \frac{a^{n}}{b^{n}}$ .

Чтобы возвести дробь в степень, надо возвести в эту степень числитель и знаменатель и первый результат записать в числителе, а второй — в знаменателе дроби.

Применение правила возведения дроби в натуральную степень

Рассмотрим пример применения правила возведения дроби в натуральную степень.

Пример 5

Возведите дробь $\frac{3 x^{2}}{2 y^{3}}$ в четвертую степень.

Решение

Воспользуемся правилом возведения дроби в степень и свойствами степеней чисел с натуральным показателем:

${(\frac{3 x^{2}}{2 y^{3}})}^{4} = \frac{(3 x^{2})^{4}}{(2 y^{3})^{4}} = \frac{3^{4} (x^{2})^{4}}{2^{4} (y^{3})^{4}} = \frac{81 x^{8}}{16 y^{12}}$ .

Ответ: $\frac{81 x^{8}}{16 y^{12}}$ .

Упражнение 2

Выполните действия с дробями:

а) ${(\frac{4 x}{3 y^{2}})}^{3}$ ; б) ${(\frac{2 k^{3}}{5 m^{3}})}^{4}$ ; в) ${(- \frac{5 a^{3}}{3 b^{4}})}^{3}$ ; г) ${(- \frac{x + 1}{2 z^{2}})}^{4}$ .

Контрольные вопросы

1. По какому правилу выполняется умножение рациональных дробей?

2. Каким образом можно умножить многочлен на рациональную дробь?

3. Сформулируйте правило умножения нескольких (более двух) рациональных дробей.

Ответы

Упражнение 1

а) $\frac{a}{3 b}$ ; б) $\frac{2 a}{x}$ ; в) $\frac{6}{x^{2}}$ ; г) 3.

Упражнение 2

а) $\frac{64 x^{3}}{27 y^{6}}$ ; б) $\frac{16 k^{12}}{625 m^{12}}$ ; в) $- \frac{125 a^{9}}{27 b^{12}}$ ; г) $\frac{{(x + 1)}^{4}}{16 z^{8}}$ .

Конспект урока: Умножение дробей. Возведение дроби в степень

Алгебраические выражения

Правило умножения дробей

Правило возведения дроби в степень