Конспект урока: Примеры комбинаторных задач

Комбинаторика

Приступим к изучению ещё одного очень важного раздела математики. Люди пользуются комбинаторикой в своей жизни, даже не замечая этого. Областей применения комбинаторных задач очень много: учебные заведения (составление расписаний), сфера общественного питания (составление меню), лингвистика (рассмотрение вариантов комбинаций букв), география (раскраска карт), спортивные соревнования (расчёт количества игр между участниками), производство (распределение нескольких видов работ между рабочими), агротехника (размещение посевов на нескольких полях). И это лишь малая часть.

Слово «комбинаторика» происходит от латинского слова combinare, которое означает «соединять, сочетать».

Перебор вариантов

Комбинаторные задачи являются задачами математики, поэтому есть несколько способов их решения. Первый из них — перебор вариантов. Его суть состоит в том, чтобы составить и выписать всевозможные варианты.

На завтрак Вова может выбрать два из пяти бутербродов, приготовленных мамой. В этот раз на тарелке лежат бутерброды с маслом, с колбасой, с сыром, с джемом, с арахисовой пастой. Сколькими способами Вова может выбрать себе завтрак.

Решение

Для начала виды бутербродов обозначим первой буквой их составляющих: М (масло), К (колбаса), С (сыр), Д (джем), П (паста).

Составим все завтраки, в которых есть бутерброд с маслом:

МК, МС, МД, МП.

Теперь выпишем завтраки с бутербродом с колбасой, но без масла:

КС, КД, КП.

Используя бутерброды с сыром, джемом и пастой, составим оставшиеся завтраки:

СД, СП.

И остался вариант бутербродов с джемом и пастой

ДП.

Осталось посчитать: $4+3+2+1=10$. То есть существует 10 способов выбрать 2 бутерброда из пяти.

Ответ: $10$.

Сколько видов мороженого можно получить, соединяя три вида из имеющихся: банан, манго, киви, дыня, пломбир, шоколад?

Дерево событий

Второй способ решения комбинаторных задач — построение дерева событий. Он очень похож на предыдущий метод, только графический.

Сколько трехзначных чисел можно составить из цифр $2, 5, 6, 9$, при условии, что цифры не могут повторяться и первая цифра обязательно чётная.

Решение

Построим дерево событий. 

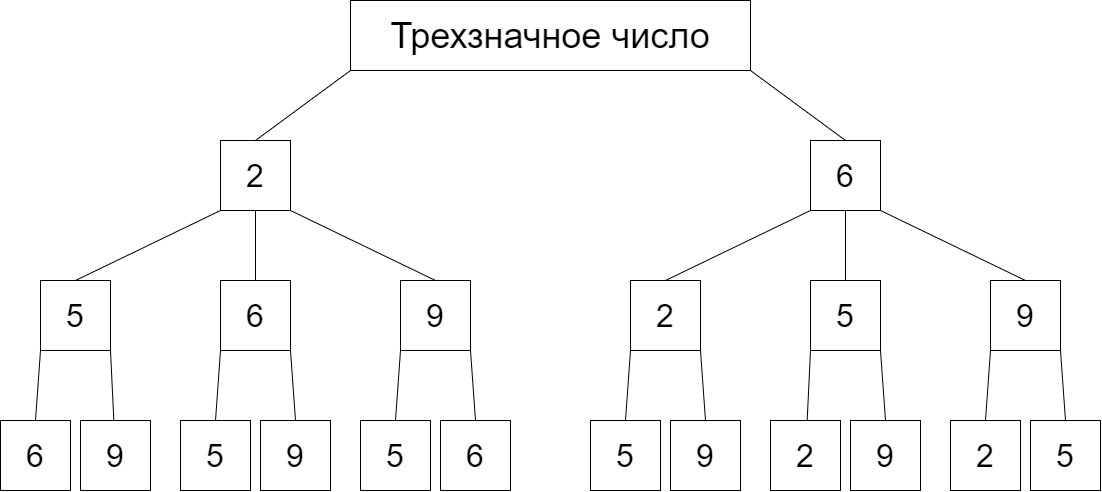
На первое место можно поставить $2$ или $6$; на второе любую из оставшихся, не повторяющих $2$ или $6$; а на третьем месте должна быть цифра, которая не повторяет две предыдущие.

Таким образом, получили $12$ чисел.

Ответ: $12$.

Сколько трёхзначных чисел можно составить из цифр $0, 1, 2, 7, 9$, если цифры не могут повторяться?

Правило умножения

Последний из способов не предполагает записи вариантов в любом виде. Этот метод — аналитический. Для решения комбинаторных задач с помощью этого способа достаточно воспользоваться комбинаторным правилом умножения . Это значительно сокращает время решения комбинаторной задачи, то при этом теряется наглядность решения.

Другими словами, чтобы получить количество различных комбинаций из конечного числа элементов нужно перемножить между собой количество способов выбора элементов на каждое место в этой комбинации.

Катя решила распланировать свой выходной день. Утром она может выйти на пробежку или сходить в бассейн; днем — встретиться с Машей или Светой, или навестить бабушку; вечером — почитать книгу, поиграть с братом на приставке, погулять с собакой или посмотреть фильм с родителями. Сколько вариантов расписания у неё могло получиться?

Решение

Утро может быть запланировано двумя вариантами, день — тремя, а вечер — с помощью четырех.

Тогда общее количество исходов равно произведению $2\times 3\times 4=24$. Т. е. $24$ варианта расписания у неё могло получиться.

Ответ: $24$.

Учителю необходимо составить тест из трех вопросов. Для этого он берет из одного сборника по одному вопросу. При этом в первом сборнике 15 вопросов, во втором — 10, а в третьем — 20. Сколько вариантов теста он может составить?

Упражнение 1

1. $20$.

Упражнение 2

1. $48$.

Упражнение 3

1. $3 000$.