Конспект урока: Функция y=x^n

Степенная функция $y=x^n$

Функциональные зависимости существуют во всех сферах жизни человека. Во многих областях науки при изучении различных явлений и процессов обнаруживается одна общая степенная зависимость между двумя переменными величинами, участвовавшими в данном процессе. 

При радиоактивном распаде, скорость распада или восстановления измеряется временем, в течение которого распадается (соответственно восстанавливается) половина вещества. По закону степенной функции размножалось бы все живое на Земле, если бы для этого имелись благоприятные условия.

Рассмотрим функцию, заданную формулой $y=x^n$, где $x$ — независимая переменная, а $n$ — натуральное число.

Степенные функции при $n=1,2$и $3$, т.е. функции $y=x$, $y=x^2$ и $y=x^3$, вы уже рассматривали. Их свойства и графики вам известны.

Выясним теперь свойства степенной функции и особенности её графика при любом натуральном $n$. Выражение $x^n$, где $n$ — натуральное число, имеет смысл при любом $x$. 

Областью определения степенной функции с натуральным показателем является множество всех действительных чисел.

Свойства степенной функции $y=x^n$ при чётном $n$

Сначала рассмотрим случай, когда показатель $n$ - чётное число. На рисунке 1 изображены графики функций $y=x^2$ и $y=x^4$.

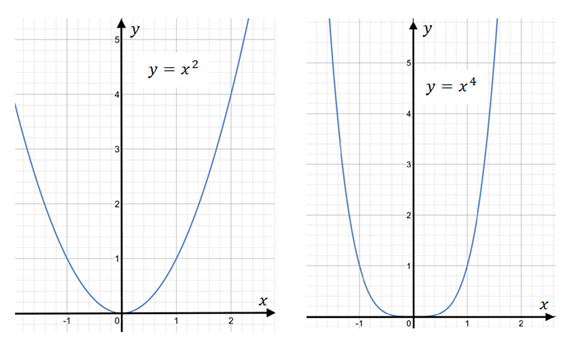Рис. 1. Графики функций y=x² и y=x⁴

Свойства функции $y=x^n$ при чётном $n$ аналогичны свойствам функции $y=x^2.$

1. Если $x=0$, то $y=0$. График функции проходит через начало координат.

2. Если $x\ne 0$, то $y>0$. Это следует из того, что чётная степень как положительного, так и отрицательного числа положительна. График функции расположен в первой и второй координатных четвертях.

3. Противоположным значениям аргумента соответствуют равные значения функции. Это следует из того, что при чётном $n$ равенство $(-x{)}^n=x^n$ верно при любых значениях $x$.

4. Функция возрастает в промежутке $[0; +\infty )$ и убывает в промежутке $(-\infty ;0]$.

5. Область значений функции есть множество неотрицательных чисел — $y \in [0; +\infty )$.

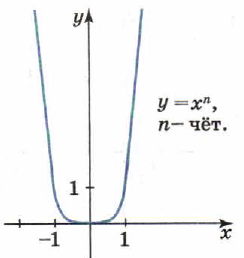Рис. 2. График функции y=xⁿ при четном показателе n

На рисунке 2 показано, как выглядит график функции $y=x^n$ при чётном показателе $n$.

 

График степенной функции $y=x^n$ при чётном показателе $n$ пересекает любая прямая $y=a$, если $a\ge 0$. Если же $a<0$, то прямая $y=a$ не пересекает график.

Свойства степенной функции $y=x^n$ при нечётном $n$

Рассмотрим случай, когда показатель $n$ — нечётное число. На рисунке 3 изображены графики функций $y=x^3$ и $y=x^5$.

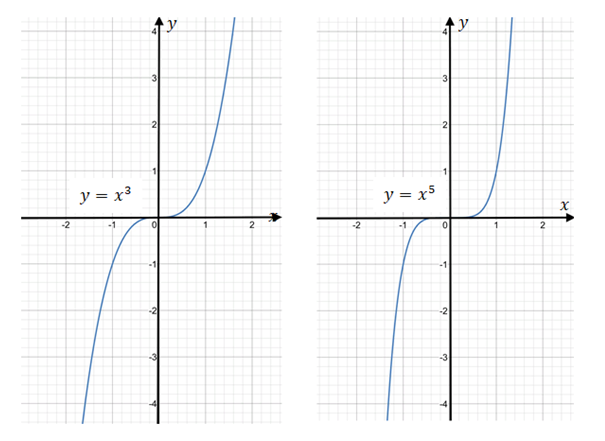Рис. 3. Графики функций y=x³ и y=x⁵

Свойства функции $y=x^n$ при нечётном $n$ аналогичны свойствам функции $y=x^3$.

1. Если $x=0$, то $y=0$. График функции проходит через начало координат.

2. Если $x>0$, то $y>0$, если $x<0$, то $y<0$. График функции расположен в первой и третьей координатных четвертях.

3. Противоположным значениям аргумента соответствуют противоположные значения функции. Это следует из того, что при нечётном $n$ для любого значения $x$ верно равенство $(-x{)}^n=-x^n$.

4. Функция возрастает на всей области определения.

5. Область значений функции есть множество всех действительных чисел.

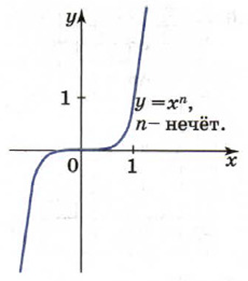Рис. 4. График функции y=xⁿ при нечётном показателе n>1

На рисунке 4 показано, как выглядит график функции $y=x^n$ при нечётном показателе $n$.

 

График степенной функции $y=x^n$  при нечётном показателе $n$ пересекает любая прямая $y=a$.

Ответы

Упражнение

 

1. а, в, г. 

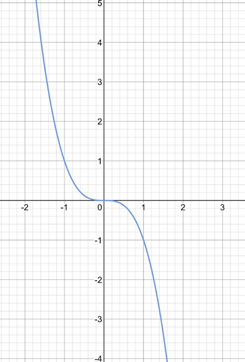
2. а) $x=0$ нуль функции; область определения $x \in (-\infty ; +\infty )$; область значений $y\in (-\infty ; +\infty );$функция убывает на всей области определения; наименьшего и наибольшего значений функции нет.

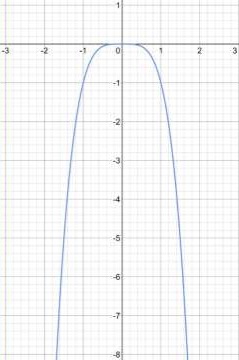
б) $x=0$ — нуль функции; область определения $x\in (-\infty ; +\infty )$; область значений $y\in (-\infty ; 0];$функция возрастает на $(-\infty ; 0]$ функция убывает на $[0; +\infty )$; наибольшее значение функции $y=0$, при $x=0;$ наименьшего значения нет.