- Квадратичная функция;
- Функция и её график в зависимости от значения ;
- Свойства функции .
- Знать определение квадратичной функции;
- Уметь строить график функции ;
- Знать свойства функции .
- Как называется график функции ?
- В чем отличие графиков функций и ?
- Как построить график функции ?
Квадратичная функция
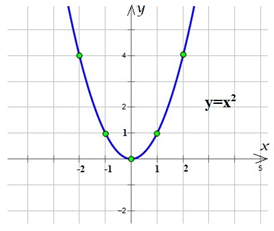 Рис. 1. График функции y=x2
Рис. 1. График функции y=x2
С несколькими функциями и их графиками вы уже знакомы. Парабола, которая служит графиком функции (рис. 1), - одна из них. Параболу можно встретить везде и не только в объектах, созданных человеком, как, например, в фонтанах, бокалах и даже сёдлах для лошади, но и в самой природе, где не касалась рука человека: в виде горных хребтов, морских заливов и в других знакомых нам объектов.
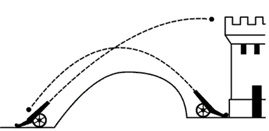 Рис. 2. Параболическая траектория
Рис. 2. Параболическая траектория
Парабола задает форму изгиба спутниковых тарелок. Также по параболической траектории летят в воздухе пушечные ядра, лыжники-фристайлеры и взмывают из воды дельфины (рис. 2).
Квадратичной функцией называется функция, которую можно задать формулой вида:
,
где - независимая переменная, , и – некоторые числа, причём .
Областью определения квадратичной функции является множество всех чисел .
Одним из самым популярных примеров квадратичной функции является зависимость координаты тела от времени при равноускоренном движении. Эта зависимость выражается формулой:
,
где (м/c2) – ускорение тела, (м/c) – начальная скорость движения, (м) - начальная координата, (c) – время, (м) – координата тела.
Если, например, , , , то
.
Функция и её график в зависимости от значения
Изучение квадратичной функции начнем с частного случая – функции .
При формула принимает вид . Об этой функции и её графике мы поговорили в самом начале (рис.1).
Построим график функции (рис.3а).
Составим таблицу значений этой функции:
|
|
-2
|
-1.5
|
-1
|
-0.5
|
0
|
0.5
|
1
|
1.5
|
2
|
|
|
16
|
9
|
4
|
1
|
0
|
1
|
4
|
9
|
16
|
При любом значения функции больше соответствующего значения функции в 4 раза. Получаем, что все точки графика функции можно получить путем перемещения точек графика функции вверх так, чтобы расстояние от оси до каждой точки увеличилось в 4 раза. Иными словами, график функции можно получить из параболы растяжением от оси в 4 раза (рис. 3. б).
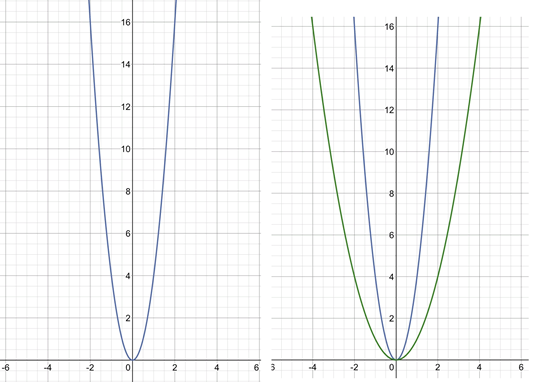 Рис. 3. а) График функции y=4x2, б) Графики функции y=4x2 и y=x2
Рис. 3. а) График функции y=4x2, б) Графики функции y=4x2 и y=x2
Теперь построим график функции и . Для этого составим таблицу значений для первой функции:
|
|
-4
|
-3
|
-2
|
-1
|
0
|
1
|
2
|
3
|
4
|
|
|
4
|
2.25
|
1
|
0.25
|
0
|
0.25
|
1
|
2.25
|
4
|
Составим таблицу значений для второй функции:
|
|
-4
|
-3
|
-2
|
-1
|
0
|
1
|
2
|
3
|
4
|
|
|
-4
|
-2.25
|
-1
|
-0.25
|
0
|
-0.25
|
-1
|
-2.25
|
-4
|
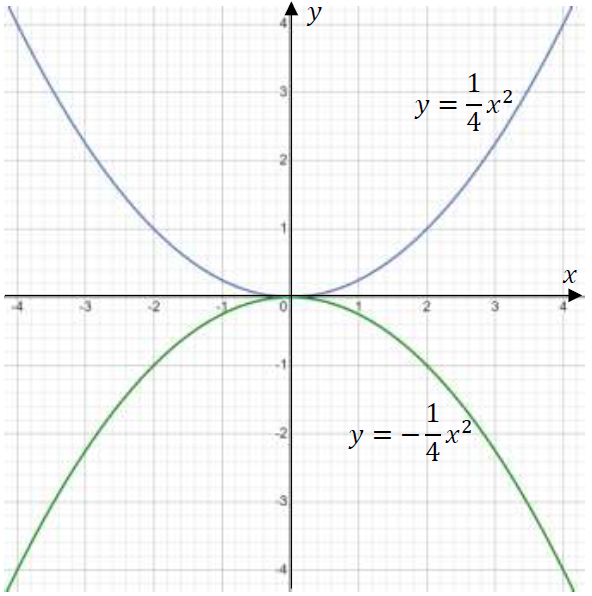 Рис. 4. Графики функций
Рис. 4. Графики функций
Построим оба графика в одной координатной плоскости (рис. 4).
Сравнив таблицы значений и графики функций и , можно увидеть, что при любом значения этих функций являются противоположными числами. Таким образом, можно сделать вывод, что графики этих функций симметричны относительно оси .
Графики функций и (при ) симметричны относительно оси .
График функции где , как и график функции называется параболой .
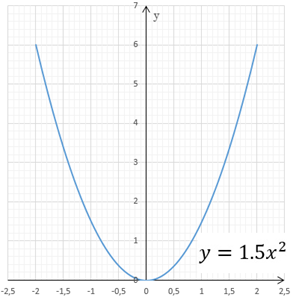
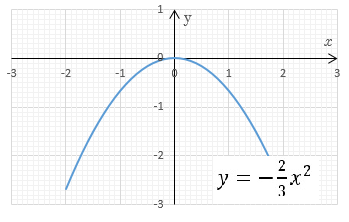
Упражнение 1
- Построить график функции .
- Построить график функции .
Свойства функции
Сформулируем свойства функции при .
1. Если , то . График функции проходит через начало координат.
2. Если , то . График расположен в верхней полуплоскости.
3. Противоположным значениям аргумента соответствуют равные значения функции. График функции симметричен относительно оси .
4. Функция убывает в промежутке и возрастает в промежутке .
5. Наименьшее значение, равное нулю, функция принимает при наибольшего значения функция не имеет.
6. Областью значений функции является промежуток .
Теперь сформулируем свойства функции при .
1. Если то . График функции проходит через начало координат.
2. Если , то . График расположен в нижней полуплоскости.
3. Противоположным значениям аргумента соответствуют равные значения функции. График функции симметричен относительно оси .
4. Функция возрастает в промежутке и убывает в промежутке .
5. Наибольшее значение, равное нулю, функция принимает при , наименьшего значения функция не имеет.
6. Областью значений функции является промежуток .
Из перечисленных свойств следует, что при ветви параболы направлены вверх, а при - вниз. Ось является осью симметрии параболы.
Точку пересечения параболы с её осью симметрии называют вершиной параболы .
График функции можно получить из графика функции с помощью симметрии относительно оси .
График функции можно получить из графика функции с помощью растяжения от оси в раз, если , и с помощью сжатия к оси в раза, если .
Упражнение 2
- Опишите свойства функции ;
- Опишите свойства функции .
Контрольные вопросы:
1. Что называют квадратичной функцией?
2. Какие свойства функции являются одинаковыми для положительных и отрицательных значений коэффициента ?
3. Как получить график функции из графика функции используя симметрию и растяжение/сжатие?
Упражнение 1
1.
2.
Упражнение 2
1. – нуль функции; область определения ; область значений ; функция возрастает в ; функция убывает в ;
наименьшее значение функции при ; наибольшего значения нет.
2. – нуль функции; область определения ; область значений ; функция возрастает в функция убывает в ;
наибольшее значение функции , при ; наименьшего значения нет.

