- Определение функции;
- Область определения и область значений функции;
- График функции;
- Линейная функция;
- Функция обратной пропорциональности;
- Графики других функций.
- Знать, что такое функция, зависимая и независимая переменные, область определения и область значений функции;
- Знать формулы, задающие линейную функцию, функцию обратной пропорциональности;
- Уметь находить значения функции по заданным значениям аргумента;
- Уметь находить область определения функции;
- Уметь определять вид графика функции.
- Приведите примеры известных вам функций.
- Какой вид имеют графики этих функций?
- Как прочитать запись ?
Определение функции
Функция – это одно из самых фундаментальных математических понятий, оно применяется во всех точных науках. Функция в общем виде – это зависимость величин. Любая физическая формула выражает зависимость одного параметра от другого. Так, связь между давлением газа и его температурой при постоянном объеме выражается формулой: .
Функцией называют такую зависимость переменной от переменной , при которой каждому значению переменной соответствует единственное значение переменной .
Переменную называют независимой переменной или аргументом. Переменную называют зависимой переменной. Значения зависимой переменной называются значениями функции.
Говорят также, что переменная является функцией от переменной .
Функция позволяет установить соответствие между двумя множествами таким образом, что каждому элементу первого множества соответствует единственный элемент второго множества. При этом данное соответствие выражается определенным правилом или законом.
Коротко зависимость от записывают так: (читают: « равно от »). Символом обозначают значение функции, соответствующее значению аргумента, равному .
В записи вида вместо можно употреблять и другие буквы: , , и т.п.
Пример 1
Функция задана формулой . Найти значения функции для значений , равных и .
Решение
Т.к. функция имеет вид , то .
Чтобы найти значение функции при заданных значениях, необходимо подставить эти значения в саму функцию вместо переменной .
Ответ:
Упражнение 1
1. Найдите значения функции вида для значений переменной
а) б) в)
2. Найдите значения функции вида для значений переменной :
а) б) в)
3. Функция имеет вид . Найти .
Область определения и область значений функции
Все значения независимой переменной образуют область определения функции.
Все значения, которые принимает зависимая переменная, образуют область значений функции.
Функция считается заданной, если указана область определения и правило, согласно которому каждому значению независимой переменной поставлено в соответствие единственное значение зависимой переменной. Областью определения функции может быть множество всех чисел, тогда пишут: . Также встречаются функции, область значений которых отличается от множества действительных чисел. Если функция имеет вид рациональной дроби, т.е. в знаменателе есть независимая переменная, то знаменатель этой дроби не должен обращаться в нуль. Если же в записи функции присутствует квадратный корень, то выражение под знаком корня должно быть неотрицательным.
Пример 2
Найдите область определения следующих функций:
а) б) в)
Решение
- Область определения первой функции – это множество действительных чисел .
- В знаменателе функции стоит выражение . Это выражение не может быть равно нулю, т.к. на нуль делить нельзя. Значит, , , т.е. область определения или .
- Функция имеет вид , следовательно выражение под корнем должно быть неотрицательное, т.е. , .
Ответ: 1) ; 2) ; 3) .
Упражнение 2
1. У какой(-их) из предложенных функций область определения – множество действительных чисел?
a)
б)
в)
2. Найдите область определения функции вида:
График функции
С понятием «график» любой человек сталкивается постоянно. У всех на слуху: график движения поезда, график продаж и график изменения температуры. Это удобная форма представления информации, которая используется в самых разных областях повседневной деятельности человека. Графики применяются во всех сферах жизнедеятельности человека. Любая зависимость может быть задана с помощью графика функции . По сути график является графической иллюстрацией некоторой зависимости.
График функции – это множество точек на координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – значениям функции.
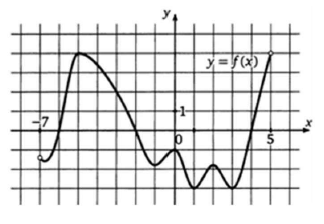 Рис. 1. График функции
Рис. 1. График функции
По графику функции можно найти области определения и значений функции, значения функции в некоторых точках, наибольшее и наименьшее значения функции.
Так на рисунке 1 изображен график функции областью определения которой является интервал . Также по графику можно найти, что , , . Наименьшее значение функции равно , а наибольшее равно . При этом любое число от до является значением данной функции, т.е. область значений функции – отрезок .
Упражнение 3
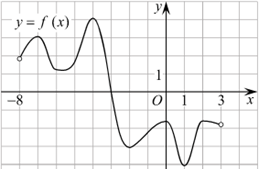 Рис. 2. График функции f(x)
Рис. 2. График функции f(x)
По графику функции (рисунок 2) определить:
1. область определения;
2. область значений;
3. ,
Линейная функция
Вы уже знакомы с некоторыми функциями, которые изучали в предыдущих классах. Первая из них – это линейная функция, задаваемая формулой , где и - некоторые числа. Вторая функция – это частный случай линейной функции или функция прямой пропорциональности, которая задана формулой , где .
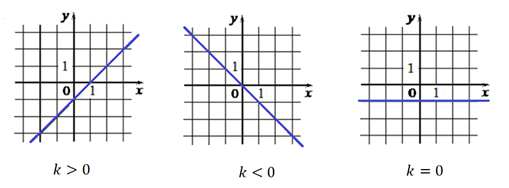 Рис. 3. График функции 𝑦 = 𝑘𝑥 + 𝑏
Рис. 3. График функции 𝑦 = 𝑘𝑥 + 𝑏
Графиком функции служит прямая (рис. 3).
Область определения этой функции – это множество действительных чисел.
Область значений этой функции – это множество действительных чисел при ; при множество значений состоит из одного числа .
Функция обратной пропорциональности
Третья функция, с которой вы уже знакомы, - это функция обратной пропорциональности, которая имеет вид , где .
Графиком функции служит гипербола (рис. 4).
Область определения и область значений этой функции одинаковые – это множество действительных чисел кроме нуля, т.е. .
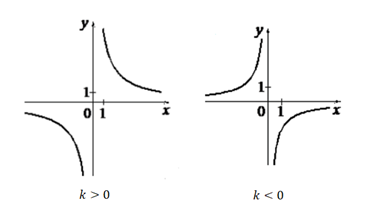 Рис. 4. График функции y = k/x
Рис. 4. График функции y = k/x
Графики некоторых функций
Ранее вы изучали функции, заданные формулами , , . Их графики изображены на рисунке 5.
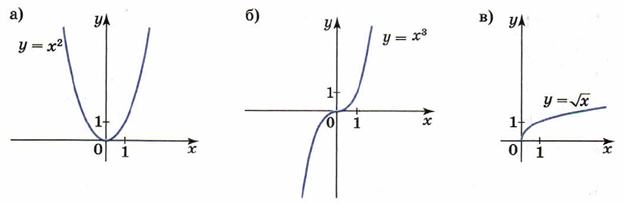 Рис. 5. Графики функций
Рис. 5. Графики функций
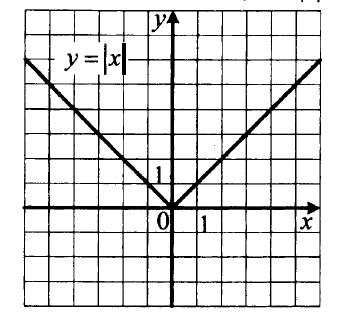 Рис. 6. График функции y = |x|
Рис. 6. График функции y = |x|
Еще одна функция, заданная формулой имеет интересный график, который вы легко можете построить, если вспомните, что такое модуль. А именно:
Графики функций и строить вы умеете. Поэтому достаточно построить графики этих функций и стереть лишнее.
Контрольные вопросы:
1. Чем отличается область определения функции от области значений?
2. Как найти значение функции при заданном значении независимой переменной?
3. Что можно определить по графику функции?
4. Что является графиком линейной функции?
5. Какая область определения у функции обратной пропорциональности?
Упражнение 1
1. а) 1; б) -29; в) 1,25. 2. а) 7; б) 25; в) 19,5. 3. -4
Упражнение 2
1. а, в 2.
Упражнение 3
1. 2. 3.

