- Затухающие и вынужденные колебания
- Амплитудно-частотная характеристика колебательной системы. Резонанс
- знать понятия: затухающие и вынужденные колебания, резонанс; физический смысл резонансной частоты
- уметь объяснять причины уменьшения амплитуды затухающих колебаний; объяснять зависимость резонансной частоты от сил трения в системе
- Как будет меняться с течением времени амплитуда и энергия колебательной системы, если учесть трение?
- По какой формуле можно рассчитать период колебаний пружинного маятника?
- Зависит ли период математического маятника от груза, висящего на нити?
Затухающие и вынужденные колебания
В предыдущем параграфе мы рассмотрели превращения энергии в колебательной системе, в которой механическая энергия системы не изменяется с течением времени. В реальных условиях на систему всегда действуют внешние силы, в том числе силы трения, поэтому получить свободные гармонические колебания в ходе эксперимента невозможно.
Пусть пружинный маятник в начале колебательного движения находится в амплитудном положении, в точке с координатой х = хmax. Начальная механическая энергия системы равна Е0.
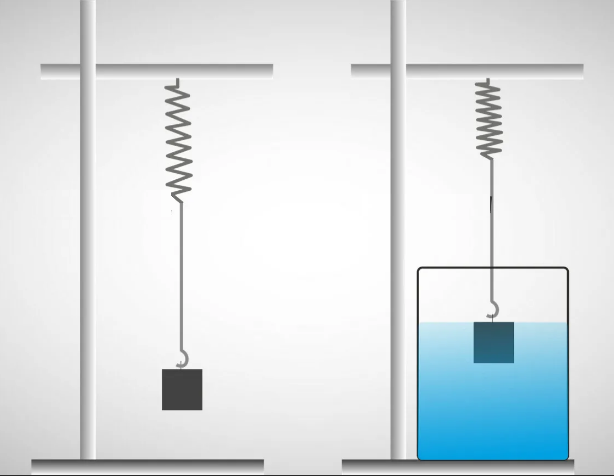 Рис. 1. Чем больше трение в колебательной системе, тем быстрее уменьшается амплитуда колебаний
Рис. 1. Чем больше трение в колебательной системе, тем быстрее уменьшается амплитуда колебаний
Если сумма работ внешних и внутренних сил трения в колебательной системе не равна нулю, то через некоторое время t механическая энергия системы будет равна
.
Если сумма работ Aтр + Aex будет меньше нуля, то механическая энергия системы будет уменьшаться: в результате с течением времени будет уменьшаться амплитуда колебаний и в некоторый момент маятник прекратит движение.
Понятно, что чем больше модуль величины , тем скорее маятник остановится.
Например, рассмотрим зависимости смещения от времени двух одинаковых маятников, один из которых находится в воздухе, а другой опущен в воду (рис. 1).
В обоих случаях механическая энергия системы будет уменьшаться, но в случае с маятником, погружённым в воду, эти изменения будут происходит намного быстрее. График зависимости смещения данных маятников от времени приведён на рисунке 2.
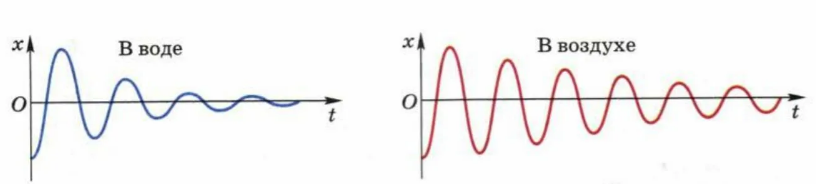 Рис. 2. График зависимости смещения одинаковых маятников, один из которых находится в воде, другой — в воздухе
Рис. 2. График зависимости смещения одинаковых маятников, один из которых находится в воде, другой — в воздухе
Представим иную ситуацию: вы раскачиваете друга на качелях, периодически прикладывая к качелям некоторую силу. В результате амплитуда колебаний качелей будет увеличиваться. Это значит, что положительная работа внешней силы, которую вы прикладываете к качелям, по модулю больше отрицательной работы силы трения , сумма этих работ положительна . В результате механическая энергия системы будет увеличиваться.
Колебания, происходящие под действием изменяющейся со временем внешней силы, называются вынужденными.
Если прикладывать к качелям внешнюю силу, равную по модулю силам трения, препятствующим движению, сумма работ этих сил будет равна нулю Aтр + Aex = 0, в этом случае механическая энергия системы не будет изменяться с течением времени: качели будут колебаться с одинаковой амплитудой.
Такие колебания называются установившимися вынужденными колебаниями. Внешнюю силу, совершающую положительную работу, равную работе сил трения, называют вынуждающей силой.
Амплитудно-частотная характеристика колебательной системы. Резонанс
Вернёмся к пружинному маятнику, погружённому в воду (рис. 1). Если на тело не будет действовать вынуждающая сила, колебания с течением времени будут затухать. Поместим под сосуд с водой электромагнит, действующий на груз маятника с периодически изменяющейся силой. При включении электромагнита первоначально покоившийся маятник начнёт колебательное движение, механическая энергия системы будет увеличиваться, но в определённый момент времени амплитуда колебаний перестанет увеличиваться и будет оставаться постоянной с течением времени — это значит, что в системе установились вынужденные колебания.
Частота установившихся вынужденных колебаний равна частоте вынуждающей силы.
Амплитуда установившихся вынужденных колебаний зависит от частоты вынуждающей силы.
Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы называется амплитудно-частотной характеристикой колебательной системы или сокращено АЧХ.
На рисунке 3 представлена амплитудно-частотная характеристика пружинного маятника, помещённого в воду.
Вынуждающая сила данного маятника изменяется по гармоническому закону с постоянной амплитудой.
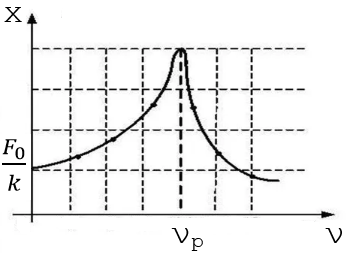 Рис. 3. Амплитудно-частотная характеристика
Рис. 3. Амплитудно-частотная характеристика
Рассмотрим представленный график. Когда частота изменений вынуждающей силы достаточно мала, а модуль вынуждающей силы достигает некоторого значения , деформация пружины изменяется на величину, равную , где k — коэффициент жёсткости пружины. Величина представляет собой амплитуду установившихся вынужденных колебаний при малой частоте .
Увеличение частоты приводит к увеличению амплитуды вынужденных колебаний. При достижении максимальной часты смещение достигает некоторого максимально возможного значения.
Если частота изменения вынуждающей силы продолжит увеличиваться, амплитуда колебаний будет уменьшаться. Это происходит по причине того, что груз вследствие своей инертности не успевает сместиться на ту величину, которой соответствует значение вынуждающей силы. Сила же очень быстро меняет направление своего действия и начинает тянуть маятник в противоположную сторону. В результате таких воздействий груз совершает колебания с очень маленькой амплитудой.
Явление достижения амплитудой установившихся вынужденных колебаний максимального значения при достижении частоты вынуждающей силой некоторого значения называется резонансом.
Частота вынуждающей силы, при которой достигается максимальное значение амплитуды колебаний, называется резонансной частотой .
Следует понимать, что увеличение амплитуды является следствием резонанса. Причина увеличения амплитуды — совпадение частоты вынуждающей силы с собственной частотой колебательной системы.
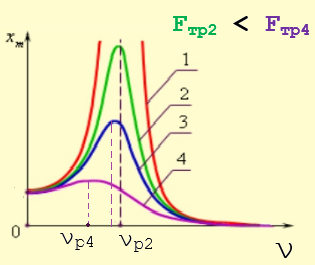 Рис. 4. Изменение резонансной частоты в зависимости от сил трения в колебательной системе
Рис. 4. Изменение резонансной частоты в зависимости от сил трения в колебательной системе
Чем больше трение в системе, тем меньше резонансная частота. Говорят, что при сильном трении резонанс «тупой», при слабом — «острый» (рис. 4).
Это объясняется тем, что при увеличении вязкого трения, а также взаимного трения между частями колебательной системы, амплитуда и скорость колебаний груза под действием вынуждающей силы уменьшаются, следовательно, резонансная частота также снижается.
Понятно, что, если трение в системе мало, амплитуда колебаний будет иметь большое значение даже при небольших значениях вынуждающей силы. Теоретически, при отсутствии трения смещение груза относительно положения равновесия будет стремиться к бесконечности — график 1 на рисунке 4. В реальных условиях изменение амплитуды колебаний при очень большой деформации перестаёт подчиняться закону Гука, такие колебания уже не будут гармоническими. Помимо этого, при очень больших деформациях колебательная система может разрушиться.
Итоги
- Колебания, происходящие под действием изменяющейся со временем внешней силы, называются вынужденными.
- Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы называется амплитудно-частотной характеристикой (АЧХ) колебательной системы.
- Явление достижения амплитудой установившихся вынужденных колебаний максимального значения при достижении частоты вынуждающей силой некоторого значения называется резонансом.
- Частота вынуждающей силы, при которой достигается максимальное значение амплитуды колебаний, называется резонансной частотой .
- При увеличении трения в системе резонансная частота уменьшается.
Контрольные вопросы
1. В каком случае колебания называют вынужденными?
2. Что такое амплитудно-частотная характеристика системы?
3. От чего зависит резонансная частота?
- Затухающие и вынужденные колебания
- Амплитудно-частотная характеристика колебательной системы. Резонанс
- знать понятия: затухающие и вынужденные колебания, резонанс; физический смысл резонансной частоты
- уметь объяснять причины уменьшения амплитуды затухающих колебаний; объяснять зависимость резонансной частоты от сил трения в системе
- Как будет меняться с течением времени амплитуда и энергия колебательной системы, если учесть трение?
- По какой формуле можно рассчитать период колебаний пружинного маятника?
- Зависит ли период математического маятника от груза, висящего на нити?
Затухающие и вынужденные колебания
В предыдущем параграфе мы рассмотрели превращения энергии в колебательной системе, в которой механическая энергия системы не изменяется с течением времени. В реальных условиях на систему всегда действуют внешние силы, в том числе силы трения, поэтому получить свободные гармонические колебания в ходе эксперимента невозможно.
Пусть пружинный маятник в начале колебательного движения находится в амплитудном положении, в точке с координатой х = хmax. Начальная механическая энергия системы равна Е0.
 Рис. 1. Чем больше трение в колебательной системе, тем быстрее уменьшается амплитуда колебаний
Рис. 1. Чем больше трение в колебательной системе, тем быстрее уменьшается амплитуда колебаний
Если сумма работ внешних и внутренних сил трения в колебательной системе не равна нулю, то через некоторое время t механическая энергия системы будет равна
.
Если сумма работ Aтр + Aex будет меньше нуля, то механическая энергия системы будет уменьшаться: в результате с течением времени будет уменьшаться амплитуда колебаний и в некоторый момент маятник прекратит движение.
Понятно, что чем больше модуль величины , тем скорее маятник остановится.
Например, рассмотрим зависимости смещения от времени двух одинаковых маятников, один из которых находится в воздухе, а другой опущен в воду (рис. 1).
В обоих случаях механическая энергия системы будет уменьшаться, но в случае с маятником, погружённым в воду, эти изменения будут происходит намного быстрее. График зависимости смещения данных маятников от времени приведён на рисунке 2.
 Рис. 2. График зависимости смещения одинаковых маятников, один из которых находится в воде, другой — в воздухе
Рис. 2. График зависимости смещения одинаковых маятников, один из которых находится в воде, другой — в воздухе
Представим иную ситуацию: вы раскачиваете друга на качелях, периодически прикладывая к качелям некоторую силу. В результате амплитуда колебаний качелей будет увеличиваться. Это значит, что положительная работа внешней силы, которую вы прикладываете к качелям, по модулю больше отрицательной работы силы трения , сумма этих работ положительна . В результате механическая энергия системы будет увеличиваться.
Колебания, происходящие под действием изменяющейся со временем внешней силы, называются вынужденными.
Если прикладывать к качелям внешнюю силу, равную по модулю силам трения, препятствующим движению, сумма работ этих сил будет равна нулю Aтр + Aex = 0, в этом случае механическая энергия системы не будет изменяться с течением времени: качели будут колебаться с одинаковой амплитудой.
Такие колебания называются установившимися вынужденными колебаниями. Внешнюю силу, совершающую положительную работу, равную работе сил трения, называют вынуждающей силой.
Амплитудно-частотная характеристика колебательной системы. Резонанс
Вернёмся к пружинному маятнику, погружённому в воду (рис. 1). Если на тело не будет действовать вынуждающая сила, колебания с течением времени будут затухать. Поместим под сосуд с водой электромагнит, действующий на груз маятника с периодически изменяющейся силой. При включении электромагнита первоначально покоившийся маятник начнёт колебательное движение, механическая энергия системы будет увеличиваться, но в определённый момент времени амплитуда колебаний перестанет увеличиваться и будет оставаться постоянной с течением времени — это значит, что в системе установились вынужденные колебания.
Частота установившихся вынужденных колебаний равна частоте вынуждающей силы.
Амплитуда установившихся вынужденных колебаний зависит от частоты вынуждающей силы.
Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы называется амплитудно-частотной характеристикой колебательной системы или сокращено АЧХ.
На рисунке 3 представлена амплитудно-частотная характеристика пружинного маятника, помещённого в воду.
Вынуждающая сила данного маятника изменяется по гармоническому закону с постоянной амплитудой.
 Рис. 3. Амплитудно-частотная характеристика
Рис. 3. Амплитудно-частотная характеристика
Рассмотрим представленный график. Когда частота изменений вынуждающей силы достаточно мала, а модуль вынуждающей силы достигает некоторого значения , деформация пружины изменяется на величину, равную , где k — коэффициент жёсткости пружины. Величина представляет собой амплитуду установившихся вынужденных колебаний при малой частоте .
Увеличение частоты приводит к увеличению амплитуды вынужденных колебаний. При достижении максимальной часты смещение достигает некоторого максимально возможного значения.
Если частота изменения вынуждающей силы продолжит увеличиваться, амплитуда колебаний будет уменьшаться. Это происходит по причине того, что груз вследствие своей инертности не успевает сместиться на ту величину, которой соответствует значение вынуждающей силы. Сила же очень быстро меняет направление своего действия и начинает тянуть маятник в противоположную сторону. В результате таких воздействий груз совершает колебания с очень маленькой амплитудой.
Явление достижения амплитудой установившихся вынужденных колебаний максимального значения при достижении частоты вынуждающей силой некоторого значения называется резонансом.
Частота вынуждающей силы, при которой достигается максимальное значение амплитуды колебаний, называется резонансной частотой .
Следует понимать, что увеличение амплитуды является следствием резонанса. Причина увеличения амплитуды — совпадение частоты вынуждающей силы с собственной частотой колебательной системы.
 Рис. 4. Изменение резонансной частоты в зависимости от сил трения в колебательной системе
Рис. 4. Изменение резонансной частоты в зависимости от сил трения в колебательной системе
Чем больше трение в системе, тем меньше резонансная частота. Говорят, что при сильном трении резонанс «тупой», при слабом — «острый» (рис. 4).
Это объясняется тем, что при увеличении вязкого трения, а также взаимного трения между частями колебательной системы, амплитуда и скорость колебаний груза под действием вынуждающей силы уменьшаются, следовательно, резонансная частота также снижается.
Понятно, что, если трение в системе мало, амплитуда колебаний будет иметь большое значение даже при небольших значениях вынуждающей силы. Теоретически, при отсутствии трения смещение груза относительно положения равновесия будет стремиться к бесконечности — график 1 на рисунке 4. В реальных условиях изменение амплитуды колебаний при очень большой деформации перестаёт подчиняться закону Гука, такие колебания уже не будут гармоническими. Помимо этого, при очень больших деформациях колебательная система может разрушиться.
Итоги
- Колебания, происходящие под действием изменяющейся со временем внешней силы, называются вынужденными.
- Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы называется амплитудно-частотной характеристикой (АЧХ) колебательной системы.
- Явление достижения амплитудой установившихся вынужденных колебаний максимального значения при достижении частоты вынуждающей силой некоторого значения называется резонансом.
- Частота вынуждающей силы, при которой достигается максимальное значение амплитуды колебаний, называется резонансной частотой .
- При увеличении трения в системе резонансная частота уменьшается.
Контрольные вопросы
1. В каком случае колебания называют вынужденными?
2. Что такое амплитудно-частотная характеристика системы?
3. От чего зависит резонансная частота?



