- Механические колебания
- Пружинный маятник
- Гармонические колебания
- Нитяной маятник
- знать понятия: колебательное движение, период и частота колебаний, гармонические колебания; из каких элементов состоят пружинный и математический маятники
- уметь описывать движение пружинного и математического маятника в процессе их колебательного движения
- Как движется тело под действием постоянной силы?
- Как будет двигаться тело, если сила, действующая на него, будет периодически изменяться?
- Что такое маятник?
Механические колебания
Согласно второму закону Ньютона, если сумма всех сил, действующих на тело, остаётся постоянной, тело движется с постоянным ускорением: оно может двигаться прямолинейно равноускоренно или равномерно, криволинейно равноускоренно или двигаться по окружности с постоянной по модулю скоростью.
Понятно, что, если равнодействующая сил, действующих на тело, будет изменяться с течением времени, будет меняться и ускорение тела. В этой статье мы познакомимся с одним из видов такого движения — колебательным.
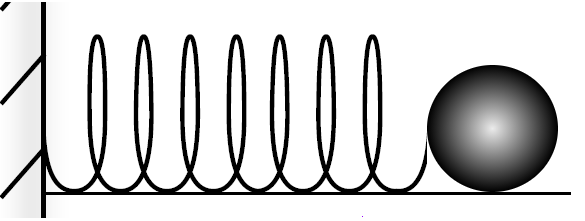 Рис. 1. Колебательная система, состоящая из пружины и прикреплённого к ней груза
Рис. 1. Колебательная система, состоящая из пружины и прикреплённого к ней груза
В повседневной жизни мы постоянно сталкиваемся с различными видами колебаний: это могут быть колебания волн на воде, колебания маятника настенных часов, колебания струн музыкальных инструментов, в результате которых мы слышим мелодию.
Рассмотрим основные характеристики механических колебаний.
Пусть шарик на пружине лежит на горизонтальной поверхности (рис. 1).
Если растянуть пружину — вывести систему из состояния равновесия — возникнет сила упругости, стремящаяся вернуть шарик с пружиной в состояние равновесия. Под действием силы упругости шарик вернётся в исходное положение, а затем по инерции продолжит движение в обратную сторону, сжимая пружину. Результатом сжатия будет возникновение противоположно направленной силы упругости, вследствие чего шарик вновь устремится к положению равновесия и т. д. Если бы в системе не было сил трения, такой цикл повторялся бы бесконечно. Понятно, что в таком процессе есть определённая периодичность: в конкретные моменты времени шарик имеет одинаковую координату, ускорение и др.
Колебательное движение — это такое движение, при котором все его характеристики периодически повторяются.
Промежуток времени, через который повторяются все характеристики колебательного движения, называется периодом колебаний Т.
Период колебаний, как и период движения по окружности, обозначается Т и в СИ измеряется в секундах (с).
Если период движения по окружности — это время, за которое материальная точка делает один оборот, то период колебательного движения — это время одного полного колебания.
Например, в приведённом примере с шариком на пружинке периодом колебаний является промежуток времени, через который шарик первый раз вернётся в исходное, крайнее правое положение. То есть тело, совершившее одно полное колебание, должно вернуться в ту же точку пространства и иметь в ней те же скорость и ускорение, что и в начале колебания.
Частота колебаний — это количество периодических колебаний в единицу времени.
Частота обозначается греческой буквой и в СИ измеряется в герцах (Гц):
1 Гц = 1 с-1.
Один герц — это частота такого колебательного движения, при котором за 1 секунду совершается 1 полное колебание.
Как и в случае с движением по окружности, частота и период являются взаимно обратными величинами:
или .
В рассмотренном примере с шариком на пружине колебательное движение осуществляется без постоянного воздействия внешних сил: достаточно лишь один раз вывести систему из состояния равновесия, сообщить ей начальный запас энергии. Такие колебания называются свободными.
Колебания в системе, обусловленные действием только внутренних сил, называются свободными.
Колебательная система — это система тел, в которой возможны свободные колебания.
Колебательная система всегда обладает положением устойчивого равновесия. Если вывести такую систему из равновесия, возникнут возвращающие силы, стремящиеся вернуть систему в первоначальное состояние.
Пружинный маятник
Пружинный маятник — это колебательная система, состоящая из упругой пружины, один конец которой жёстко закреплён, а на втором находится груз массы m. Пусть шарик с пружиной находятся на гладкой поверхности стола
(рис. 2).
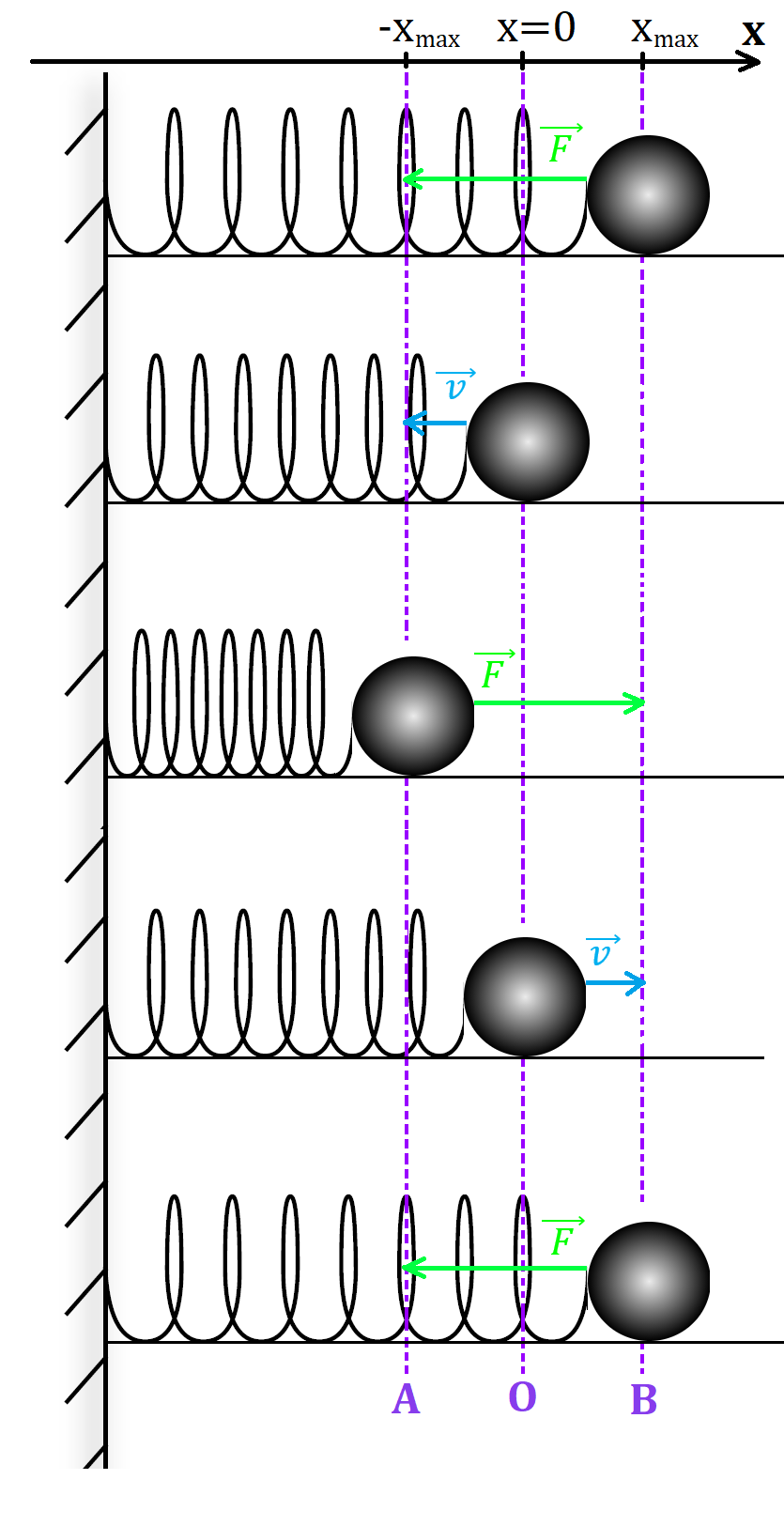 Рис. 2. Положение пружинного маятника в разные моменты времени
Рис. 2. Положение пружинного маятника в разные моменты времени
Так как поверхность стола гладкая, трение в данной системе не влияет на характер колебательного движения. Сила тяжести и сила реакции опоры в данном случае равны по модулю и противоположны по направлению — эти силы уравновешивают друг друга. Следовательно, причиной колебательного движения является только сила упругости, возникающая в пружине при её растяжении или сжатии.
Ось ОХ направим вдоль поверхности стола, начало отсчёта совместим с точкой О — положением устойчивого равновесия системы.
Шарик может отклоняться влево и вправо от положения равновесия.
Отклонение тела от положения равновесия называется смещением.
В рассматриваемой системе максимальное по модулю смещение равно хmax: когда пружина растягивается, смещение положительно, когда сжимается — отрицательно.
Сообщим системе начальный запас энергии, для этого растянем шарик с пружиной так, чтобы он оказался в точке с координатой хmax. Пока мы удерживаем шарик в таком положении, его скорость равна нулю = 0. В пружине возникает возвращающая сила упругости, направленная в сторону, противоположную смещению. Пока шарик находится в крайнем правом положении, проекция силы упругости равна:
.
Опустим шарик и включим секундомер. Под действием силы упругости пружина начнёт сжиматься, шарик будет двигаться к положению равновесия. Модуль силы упругости пропорционален величине деформации (смещению), поэтому при приближении к положению равновесия модуль силы упругости будет уменьшаться. Когда шарик достигнет координаты х = 0, сила упругости окажется равной нулю Fупр = 0, так как в состоянии равновесия пружина не деформирована. В то же время в процессе движения от точки В к точке О скорость шарика увеличится до некоторого максимально возможного значения скорости . Поэтому, достигнув положения равновесия, шарик не остановится, а продолжит движение в сторону точки А.
При движении тела от точки О к точке А пружина сжимается, возникает сила упругости, равная , значение которой будет расти по мере приближения к крайнему левому положению. Сила упругости будет препятствовать деформации, поэтому скорость шарика начнёт снижаться.
Когда шарик окажется в координате -хmax, соответствующей точке А, скорость тела будет равна нулю = 0. На шарик будет действовать сила упругости, направленная в сторону положения равновесия, проекция данной силы будет равна
.
Сила упругости, возникшая в сжатой пружине, начнёт выталкивать шарик к положению равновесия. По мере приближения к положению равновесия скорость тела будет расти, а смещение и сила упругости уменьшаться. Достигнув положения равновесия, шарик вновь будет иметь скорость , а сила упругости в пружине уменьшится до нуля Fупр = 0.
Благодаря запасу кинетической энергии шарик продолжит движение в сторону точки В, растягивая пружину и теряя скорость из-за возрастающей силы упругости. В точке В, соответствующей координате хmax, скорость тела упадёт до нуля = 0, а сила упругости будет иметь максимальное значение, проекция силы будет равна:
.
Таким образом, шарик оказался в исходном положении, а время, которое покажет секундомер, будет соответствовать периоду колебания.
Если в системе отсутствуют силы трения, процесс будет повторяться вновь и вновь: шарик будет бесконечно колебаться между точками с координатами -хmax и хmax.
Модуль максимального смещения тела при периодическом колебательном движении называется амплитудой колебаний.
В нашем примере амплитуда колебаний равна значению хmax.
Гармонические колебания
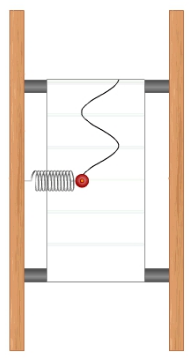 Рис. 3. Получение графической зависимости смещения от времени
Рис. 3. Получение графической зависимости смещения от времени
Прикрепим к колеблющемуся на пружинке шарику карандаш и расположим пружинный маятник над бумажной лентой (рис. 3). Если в процессе колебательного движения пружинного маятника равномерно тянуть бумажную ленту перпендикулярно направлению колебаний, мы получим характерный рисунок — волнообразную линию. Полученная картина представляет собой графическую зависимость координаты маятника от времени х(t).
На рисунке 4 изображён пример зависимости х(t) для маятника, который начал движение из амплитудного положения.
Кривая подобного вида в зависимости от начальной координаты называется косинусоида или синусоида.
Подробнее с данными графиками вы познакомитесь на математике.
Колебания, при которых зависимость смещения от времени представляет собой косинусоиду или синусоиду, называются гармоническими колебаниями.
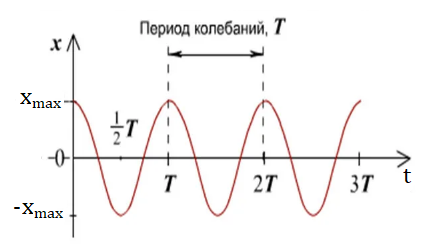 Рис. 4. Зависимость координаты от времени при гармонических колебаниях
Рис. 4. Зависимость координаты от времени при гармонических колебаниях
Гармонические колебания происходят под действием только возвращающей силы, при этом последняя должна удовлетворять двум условиям:
1. Модуль возвращающей силы должен быть пропорционален смещению тела.
2. Направление возвращающей силы противоположно направлению смещения.
Нитяной маятник
Нитяной маятник представляет собой подвешенный на нити шарик (рис. 5). Положение 2 соответствует положению устойчивого равновесия.
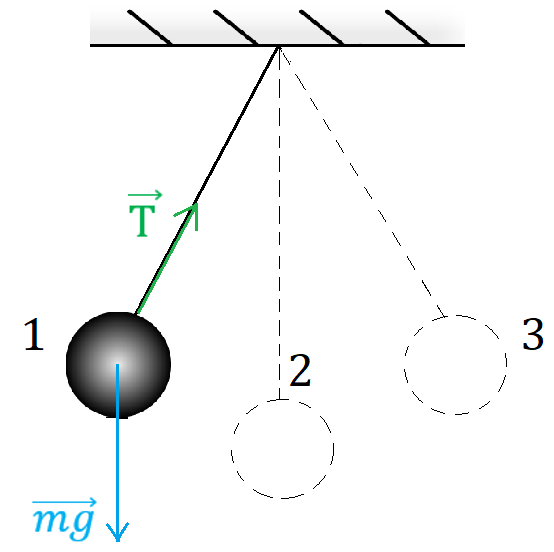 Рис. 5. Нитяной маятник
Рис. 5. Нитяной маятник
Если вывести маятник из положения равновесия, отклонить его так, чтобы он оказался в положении 1, на него начнёт действовать возвращающая сила, которая в данном случае равна сумме силы тяжести и силы натяжения нити . Под действием возвращающей силы шарик будет двигаться к положению равновесия 2, достигнув его, шарик разовьёт максимально возможную в данных условиях скорость и продолжит движение к положению 3.
Сумма сил и в положении равновесия равна нулю, но по мере приближения к положению 3 возвращающая сила будет расти, а скорость шарика уменьшаться вплоть до нуля.
Оказавшись в положении 3, шарик остановится, а затем начнёт движение в обратную сторону.
Зависимость смещения координаты реального нитяного маятника от времени не является ни синусоидой, ни косинусоидой: нитяной маятник совершает негармонические колебания.
Если растяжение нити в процессе колебаний ничтожно мало, размеры нити много больше размеров шарика, а масса шарика много больше массы нити, то шарик можно принять за материальную точку, сам маятник в этом случае называется математическим.
Математическим маятником называется материальная точка, совершающая колебания под действием силы тяжести на невесомой нерастяжимой нити, второй конец которой жёстко закреплён.
В случае, если в системе отсутствуют силы трения, а амплитуда колебаний достаточно мала, колебания математического маятника можно считать гармоническими.
Итоги
- Колебательное движение — это такое движение, при котором все его характеристики периодически повторяются.
- Промежуток времени, через который повторяются все характеристики колебательного движения, называется периодом колебаний Т. Частота колебаний — это количество периодических колебаний в единицу времени. Частота и период связаны следующим соотношением: .
- Колебания в системе, обусловленные действием только внутренних сил, называются свободными.
- Колебательная система — это система тел, в которой возможны свободные колебания.
- Модуль максимального смещения тела при периодическом колебательном движении называется амплитудой колебаний.
- Колебания, при которых зависимость смещения от времени представляет собой косинусоиду или синусоиду, называются гармоническими колебаниями.
Контрольные вопросы
1. Опишите этапы, которые проходит пружинный маятник в процессе одного полного колебания.
2. Что такое амплитуда колебаний?
3. Какие колебания называются гармоническими?
4. Что такое математический маятник?
5. Чему равна частота колебаний пружинного маятника, если период равен 5 с?
- Механические колебания
- Пружинный маятник
- Гармонические колебания
- Нитяной маятник
- знать понятия: колебательное движение, период и частота колебаний, гармонические колебания; из каких элементов состоят пружинный и математический маятники
- уметь описывать движение пружинного и математического маятника в процессе их колебательного движения
- Как движется тело под действием постоянной силы?
- Как будет двигаться тело, если сила, действующая на него, будет периодически изменяться?
- Что такое маятник?
Механические колебания
Согласно второму закону Ньютона, если сумма всех сил, действующих на тело, остаётся постоянной, тело движется с постоянным ускорением: оно может двигаться прямолинейно равноускоренно или равномерно, криволинейно равноускоренно или двигаться по окружности с постоянной по модулю скоростью.
Понятно, что, если равнодействующая сил, действующих на тело, будет изменяться с течением времени, будет меняться и ускорение тела. В этой статье мы познакомимся с одним из видов такого движения — колебательным.
 Рис. 1. Колебательная система, состоящая из пружины и прикреплённого к ней груза
Рис. 1. Колебательная система, состоящая из пружины и прикреплённого к ней груза
В повседневной жизни мы постоянно сталкиваемся с различными видами колебаний: это могут быть колебания волн на воде, колебания маятника настенных часов, колебания струн музыкальных инструментов, в результате которых мы слышим мелодию.
Рассмотрим основные характеристики механических колебаний.
Пусть шарик на пружине лежит на горизонтальной поверхности (рис. 1).
Если растянуть пружину — вывести систему из состояния равновесия — возникнет сила упругости, стремящаяся вернуть шарик с пружиной в состояние равновесия. Под действием силы упругости шарик вернётся в исходное положение, а затем по инерции продолжит движение в обратную сторону, сжимая пружину. Результатом сжатия будет возникновение противоположно направленной силы упругости, вследствие чего шарик вновь устремится к положению равновесия и т. д. Если бы в системе не было сил трения, такой цикл повторялся бы бесконечно. Понятно, что в таком процессе есть определённая периодичность: в конкретные моменты времени шарик имеет одинаковую координату, ускорение и др.
Колебательное движение — это такое движение, при котором все его характеристики периодически повторяются.
Промежуток времени, через который повторяются все характеристики колебательного движения, называется периодом колебаний Т.
Период колебаний, как и период движения по окружности, обозначается Т и в СИ измеряется в секундах (с).
Если период движения по окружности — это время, за которое материальная точка делает один оборот, то период колебательного движения — это время одного полного колебания.
Например, в приведённом примере с шариком на пружинке периодом колебаний является промежуток времени, через который шарик первый раз вернётся в исходное, крайнее правое положение. То есть тело, совершившее одно полное колебание, должно вернуться в ту же точку пространства и иметь в ней те же скорость и ускорение, что и в начале колебания.
Частота колебаний — это количество периодических колебаний в единицу времени.
Частота обозначается греческой буквой и в СИ измеряется в герцах (Гц):
1 Гц = 1 с-1.
Один герц — это частота такого колебательного движения, при котором за 1 секунду совершается 1 полное колебание.
Как и в случае с движением по окружности, частота и период являются взаимно обратными величинами:
или .
В рассмотренном примере с шариком на пружине колебательное движение осуществляется без постоянного воздействия внешних сил: достаточно лишь один раз вывести систему из состояния равновесия, сообщить ей начальный запас энергии. Такие колебания называются свободными.
Колебания в системе, обусловленные действием только внутренних сил, называются свободными.
Колебательная система — это система тел, в которой возможны свободные колебания.
Колебательная система всегда обладает положением устойчивого равновесия. Если вывести такую систему из равновесия, возникнут возвращающие силы, стремящиеся вернуть систему в первоначальное состояние.
Пружинный маятник
Пружинный маятник — это колебательная система, состоящая из упругой пружины, один конец которой жёстко закреплён, а на втором находится груз массы m. Пусть шарик с пружиной находятся на гладкой поверхности стола
(рис. 2).
 Рис. 2. Положение пружинного маятника в разные моменты времени
Рис. 2. Положение пружинного маятника в разные моменты времени
Так как поверхность стола гладкая, трение в данной системе не влияет на характер колебательного движения. Сила тяжести и сила реакции опоры в данном случае равны по модулю и противоположны по направлению — эти силы уравновешивают друг друга. Следовательно, причиной колебательного движения является только сила упругости, возникающая в пружине при её растяжении или сжатии.
Ось ОХ направим вдоль поверхности стола, начало отсчёта совместим с точкой О — положением устойчивого равновесия системы.
Шарик может отклоняться влево и вправо от положения равновесия.
Отклонение тела от положения равновесия называется смещением.
В рассматриваемой системе максимальное по модулю смещение равно хmax: когда пружина растягивается, смещение положительно, когда сжимается — отрицательно.
Сообщим системе начальный запас энергии, для этого растянем шарик с пружиной так, чтобы он оказался в точке с координатой хmax. Пока мы удерживаем шарик в таком положении, его скорость равна нулю = 0. В пружине возникает возвращающая сила упругости, направленная в сторону, противоположную смещению. Пока шарик находится в крайнем правом положении, проекция силы упругости равна:
.
Опустим шарик и включим секундомер. Под действием силы упругости пружина начнёт сжиматься, шарик будет двигаться к положению равновесия. Модуль силы упругости пропорционален величине деформации (смещению), поэтому при приближении к положению равновесия модуль силы упругости будет уменьшаться. Когда шарик достигнет координаты х = 0, сила упругости окажется равной нулю Fупр = 0, так как в состоянии равновесия пружина не деформирована. В то же время в процессе движения от точки В к точке О скорость шарика увеличится до некоторого максимально возможного значения скорости . Поэтому, достигнув положения равновесия, шарик не остановится, а продолжит движение в сторону точки А.
При движении тела от точки О к точке А пружина сжимается, возникает сила упругости, равная , значение которой будет расти по мере приближения к крайнему левому положению. Сила упругости будет препятствовать деформации, поэтому скорость шарика начнёт снижаться.
Когда шарик окажется в координате -хmax, соответствующей точке А, скорость тела будет равна нулю = 0. На шарик будет действовать сила упругости, направленная в сторону положения равновесия, проекция данной силы будет равна
.
Сила упругости, возникшая в сжатой пружине, начнёт выталкивать шарик к положению равновесия. По мере приближения к положению равновесия скорость тела будет расти, а смещение и сила упругости уменьшаться. Достигнув положения равновесия, шарик вновь будет иметь скорость , а сила упругости в пружине уменьшится до нуля Fупр = 0.
Благодаря запасу кинетической энергии шарик продолжит движение в сторону точки В, растягивая пружину и теряя скорость из-за возрастающей силы упругости. В точке В, соответствующей координате хmax, скорость тела упадёт до нуля = 0, а сила упругости будет иметь максимальное значение, проекция силы будет равна:
.
Таким образом, шарик оказался в исходном положении, а время, которое покажет секундомер, будет соответствовать периоду колебания.
Если в системе отсутствуют силы трения, процесс будет повторяться вновь и вновь: шарик будет бесконечно колебаться между точками с координатами -хmax и хmax.
Модуль максимального смещения тела при периодическом колебательном движении называется амплитудой колебаний.
В нашем примере амплитуда колебаний равна значению хmax.
Гармонические колебания
 Рис. 3. Получение графической зависимости смещения от времени
Рис. 3. Получение графической зависимости смещения от времени
Прикрепим к колеблющемуся на пружинке шарику карандаш и расположим пружинный маятник над бумажной лентой (рис. 3). Если в процессе колебательного движения пружинного маятника равномерно тянуть бумажную ленту перпендикулярно направлению колебаний, мы получим характерный рисунок — волнообразную линию. Полученная картина представляет собой графическую зависимость координаты маятника от времени х(t).
На рисунке 4 изображён пример зависимости х(t) для маятника, который начал движение из амплитудного положения.
Кривая подобного вида в зависимости от начальной координаты называется косинусоида или синусоида.
Подробнее с данными графиками вы познакомитесь на математике.
Колебания, при которых зависимость смещения от времени представляет собой косинусоиду или синусоиду, называются гармоническими колебаниями.
 Рис. 4. Зависимость координаты от времени при гармонических колебаниях
Рис. 4. Зависимость координаты от времени при гармонических колебаниях
Гармонические колебания происходят под действием только возвращающей силы, при этом последняя должна удовлетворять двум условиям:
1. Модуль возвращающей силы должен быть пропорционален смещению тела.
2. Направление возвращающей силы противоположно направлению смещения.
Нитяной маятник
Нитяной маятник представляет собой подвешенный на нити шарик (рис. 5). Положение 2 соответствует положению устойчивого равновесия.
 Рис. 5. Нитяной маятник
Рис. 5. Нитяной маятник
Если вывести маятник из положения равновесия, отклонить его так, чтобы он оказался в положении 1, на него начнёт действовать возвращающая сила, которая в данном случае равна сумме силы тяжести и силы натяжения нити . Под действием возвращающей силы шарик будет двигаться к положению равновесия 2, достигнув его, шарик разовьёт максимально возможную в данных условиях скорость и продолжит движение к положению 3.
Сумма сил и в положении равновесия равна нулю, но по мере приближения к положению 3 возвращающая сила будет расти, а скорость шарика уменьшаться вплоть до нуля.
Оказавшись в положении 3, шарик остановится, а затем начнёт движение в обратную сторону.
Зависимость смещения координаты реального нитяного маятника от времени не является ни синусоидой, ни косинусоидой: нитяной маятник совершает негармонические колебания.
Если растяжение нити в процессе колебаний ничтожно мало, размеры нити много больше размеров шарика, а масса шарика много больше массы нити, то шарик можно принять за материальную точку, сам маятник в этом случае называется математическим.
Математическим маятником называется материальная точка, совершающая колебания под действием силы тяжести на невесомой нерастяжимой нити, второй конец которой жёстко закреплён.
В случае, если в системе отсутствуют силы трения, а амплитуда колебаний достаточно мала, колебания математического маятника можно считать гармоническими.
Итоги
- Колебательное движение — это такое движение, при котором все его характеристики периодически повторяются.
- Промежуток времени, через который повторяются все характеристики колебательного движения, называется периодом колебаний Т. Частота колебаний — это количество периодических колебаний в единицу времени. Частота и период связаны следующим соотношением: .
- Колебания в системе, обусловленные действием только внутренних сил, называются свободными.
- Колебательная система — это система тел, в которой возможны свободные колебания.
- Модуль максимального смещения тела при периодическом колебательном движении называется амплитудой колебаний.
- Колебания, при которых зависимость смещения от времени представляет собой косинусоиду или синусоиду, называются гармоническими колебаниями.
Контрольные вопросы
1. Опишите этапы, которые проходит пружинный маятник в процессе одного полного колебания.
2. Что такое амплитуда колебаний?
3. Какие колебания называются гармоническими?
4. Что такое математический маятник?
5. Чему равна частота колебаний пружинного маятника, если период равен 5 с?



