- Взаимодействие тел. Третий закон Ньютона
- Примеры решения задач
- знать формулировку третьего закона Ньютона
- уметь решать задачи на движение взаимодействующих тел
- Сформулируйте первый и второй законы Ньютона.
- Куда направлен вес тела?
- С какой силой человек массой 60 кг притягивает к себе Землю?
Взаимодействие тел. Третий закон Ньютона
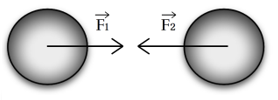 Рис. 1. Взаимное притяжение двух тел
Рис. 1. Взаимное притяжение двух тел
Вам уже известно, что если одно тело действует на другое с некоторой силой, то и второе тело также будет действовать на первое с той же самой силой. Так, если Земля притягивает к себе тело, расположенное на её поверхности, то и данное тело тоже будет притягивать к себе Землю (рис. 1).
Взаимодействие двух тел описывается третьим законом Ньютона.
Третий закон Ньютона: в инерциальной системе отсчёта два тела взаимодействуют с силами и , равными по модулю, противоположными по направлению и лежащими вдоль одной прямой: .
Отметим, что силы, с которыми взаимодействуют два тела, всегда имеют одинаковую природу, но не уравновешивают друг друга. Силы взаимодействия приложены к разным телам: сила , с которой Земля притягивает человека, приложена к человеку; сила , с которой человек притягивает Землю, — к Земле, поэтому силы и не уравновешивают друг друга.
Совместное использование второго и третьего законов Ньютона позволяет решать задачи о движении взаимодействующих тел.
Примеры решения задач
Решение задач о движении взаимодействующих тел схоже с решением задач о движении под действием нескольких сил, рассмотренным в предыдущей статье.
Но в данном случае второй закон Ньютона необходимо записывать для каждого тела, участвующего во взаимодействии.
Помимо этого, добавляется новый пункт, в котором следует записать третий закон Ньютона для рассматриваемых в задаче тел.
Алгоритм решения задач о движении взаимодействующих тел выглядит следующим образом:
- Определить, является ли движение рассматриваемых тел поступательным, ответить на вопрос: «Можно ли принять их за материальные точки?»
- Выбрать инерциальную систему отсчёта. Сделать чертёж с изображением всех сил, действующих на тела, которые участвуют во взаимодействии.
- Записать второй закон Ньютона в векторной форме для каждого тела.
- Записать второй закон Ньютона в проекциях на координатные оси для каждого тела.
- Записать третий закон Ньютона.
- Решить полученную систему алгебраических уравнений.
Пример 1
На горизонтальном полу лифта лежит ящик массой 80 кг. Лифт начинает подниматься на верхний этаж с ускорением 0,2 м/с2. Найти вес ящика при движении лифта.
Решение
1. В результате движения лифта система начнёт поступательное движение, поэтому ящик можно принять за материальную точку.
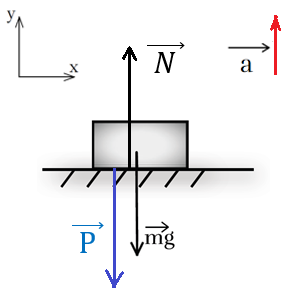 Рис. 2. Иллюстрация к примеру 1
Рис. 2. Иллюстрация к примеру 1
2. Пусть ось ОХ направлена вправо, ось
OY — вертикально вверх.
На ящик действуют две силы: сила тяжести и сила реакции опоры. На поверхность со стороны ящика действует только одна
сила — его вес (рис. 2). Так как система движется вверх, вектор ускорения также направлен вертикально вверх.
3. Второй закон Ньютона в векторной форме для ящика имеет следующий вид:
.
4. Запишем второй закон Ньютона в проекциях на координатные оси: в данном случае проекции сил и ускорения на ось ОХ равны нулю, поэтому достаточно записать проекцию на ось ординат:
.
5. В рассматриваемой задаче взаимодействуют ящик и горизонтальная поверхность лифта: ящик действует на поверхность с силой, равной его весу, поверхность — с силой реакции опоры. По третьему закону Ньютона эти силы равны по модулю и противоположны по направлению:
.
6. Решаем систему уравнений:
.
Используя метод подстановки, выражаем искомую силу Р:
.
Ответ: .
Пример 2
Два бруска удерживаются на плоскости, поверхность которой наклонена под углом 60° к горизонту. Масса брусков одинакова и равна 4 кг. Коэффициент трения между первым бруском и поверхностью равен 0,6. Второй брусок гладкий. После того, как бруски отпускают, они приходят в движение. Рассчитайте, с какой силой второй брусок действует на первый в процессе их совместного движения.
Решение
1. После того, как бруски перестают удерживать на наклонной плоскости, они начинают двигаться поступательно, поэтому оба тела можно принять за материальные точки.
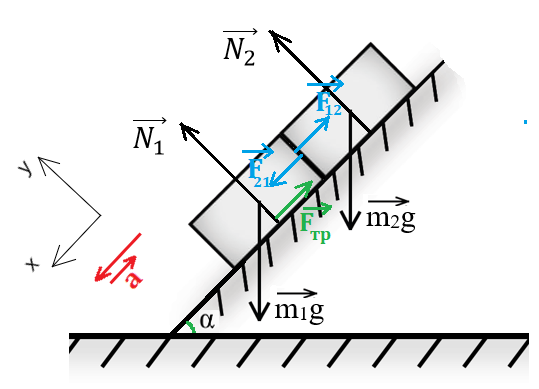 Рис. 3. Иллюстрация к примеру 2
Рис. 3. Иллюстрация к примеру 2
2. В качестве тела отсчёта выберем неподвижную наклонную плоскость. Пусть ось ОХ направлена в сторону движения брусков вдоль поверхности (рис. 3), ось OY — перпендикулярно оси ОХ.
Массы первого и второго брусков обозначим m1 и m2 соответственно. Вектор ускорения направлен в сторону движения брусков. Силы, с которыми взаимодействуют бруски 1 и 2 обозначим как и .
3. Запишем второй закон Ньютона в векторной форме для первого и для второго тела:
;
.
4. Запишем второй закон Ньютона для каждого из тел в проекциях на координатные оси. Учтём, что в выбранной системе отсчёта проекция ускорения на ось ординат равна нулю.
;
;
;
.
Найдём проекции силы тяжести на координатные оси.
5. Согласно третьему закону Ньютона, силы и направлены в противоположные стороны и равны по модулю:
.
6. Известно, что сила трения по определению равна произведению коэффициента трения на силу реакции опоры:
.
Сведём все полученные закономерности в следующую систему уравнений:
.
Используя метод подстановки, выражаем искомую силу F:
.
Ответ: .
Пример 3
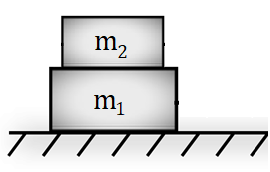 Рис. 4. Иллюстрация к примеру 3
Рис. 4. Иллюстрация к примеру 3
На гладкой горизонтальной поверхности друг на друге лежат два бруска (рис. 4). Коэффициент трения между брусками равен 0,4.
Определите, с какой минимальной силой F надо подействовать на брусок массой m1, чтобы брусок массой m2 начал по нему скользить. Массы брусков равны m1 = 5 кг и m2 = 2 кг.
Решение
1. Пусть бруски двигаются поступательно, поэтому оба тела можно принять за материальные точки.
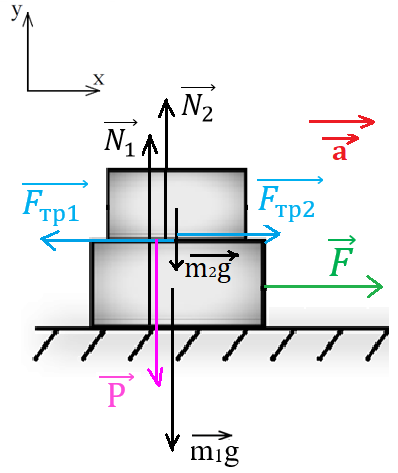 Рис. 5. Иллюстрация к примеру 3: силы, действующие на бруски
Рис. 5. Иллюстрация к примеру 3: силы, действующие на бруски
2. В качестве тела отсчёта выберем неподвижную плоскость, на которой лежат бруски. Пусть ось ОХ направлена в сторону движения брусков вдоль поверхности
(рис. 5), ось OY — перпендикулярно оси ОХ. Вектор ускорения направлен в сторону движения брусков. В месте соприкосновения брусков возникают силы трения, препятствующие взаимному движению и .
На брусок массой m1 действуют сила тяжести, сила реакции опоры, сила F, а также сила трения и вес, создаваемый бруском массой m2.
На брусок массой m2 действуют сила тяжести, сила реакции опоры и сила трения, возникающая в процессе взаимного движения.
3. Запишем второй закон Ньютона в векторной форме для первого и для второго тела:
;
.
4. Запишем второй закон Ньютона для каждого из тел в проекциях на координатные оси. Учтём, что в выбранной системе отсчёта проекция ускорения на ось ординат равна нулю:
;
;
;
.
5. Согласно третьему закону Ньютона, силы и направлены в противоположные стороны и равны по модулю:
.
Следует понимать, что в данном случае Fтр1 не зависит от N1, так как данная сила возникает не из-за трения тела m1 о поверхность, а является следствием трения брусков друг о друга, поэтому Fтр1 определяется силой реакции опоры, действующей на верхний брусок N2.
Аналогичные рассуждения применимы к паре сил и , по третьему закону Ньютона эти силы равны по модулю:
.
6. Запишем формулу силы трения:
.
Сведём все полученные соотношения в следующую систему уравнений:
.
Используя метод подстановки, выражаем искомую силу F:
.
Ответ: .
Упражнение 1
1. На горизонтальном полу лифта лежит ящик массой 10 кг. Лифт начинает опускаться на нижний этаж с ускорением 0,4 м/с2. Найти вес ящика в процессе движения лифта.
2. На наклонной плоскости длиной 5 м и высотой 4 м находится груз массой 40 кг. Какую силу, направленную вдоль плоскости, необходимо приложить, чтобы тянуть груз с ускорением 2 м/с2? Коэффициент трения 0,4.
Контрольные вопросы
1. Сформулируйте третий закон Ньютона.
2. На полу лифта на весах находится ящик. Как изменятся показания весов, когда лифт начнёт опускаться на нижний этаж с некоторым ускорением?
3. Как направлена сила трения, если брусок покоится на наклонной плоскости?
Упражнение 1
1. Р = 96 Н
2. F = 496 Н
- Взаимодействие тел. Третий закон Ньютона
- Примеры решения задач
- знать формулировку третьего закона Ньютона
- уметь решать задачи на движение взаимодействующих тел
- Сформулируйте первый и второй законы Ньютона.
- Куда направлен вес тела?
- С какой силой человек массой 60 кг притягивает к себе Землю?
Взаимодействие тел. Третий закон Ньютона
 Рис. 1. Взаимное притяжение двух тел
Рис. 1. Взаимное притяжение двух тел
Вам уже известно, что если одно тело действует на другое с некоторой силой, то и второе тело также будет действовать на первое с той же самой силой. Так, если Земля притягивает к себе тело, расположенное на её поверхности, то и данное тело тоже будет притягивать к себе Землю (рис. 1).
Взаимодействие двух тел описывается третьим законом Ньютона.
Третий закон Ньютона: в инерциальной системе отсчёта два тела взаимодействуют с силами и , равными по модулю, противоположными по направлению и лежащими вдоль одной прямой: .
Отметим, что силы, с которыми взаимодействуют два тела, всегда имеют одинаковую природу, но не уравновешивают друг друга. Силы взаимодействия приложены к разным телам: сила , с которой Земля притягивает человека, приложена к человеку; сила , с которой человек притягивает Землю, — к Земле, поэтому силы и не уравновешивают друг друга.
Совместное использование второго и третьего законов Ньютона позволяет решать задачи о движении взаимодействующих тел.
Примеры решения задач
Решение задач о движении взаимодействующих тел схоже с решением задач о движении под действием нескольких сил, рассмотренным в предыдущей статье.
Но в данном случае второй закон Ньютона необходимо записывать для каждого тела, участвующего во взаимодействии.
Помимо этого, добавляется новый пункт, в котором следует записать третий закон Ньютона для рассматриваемых в задаче тел.
Алгоритм решения задач о движении взаимодействующих тел выглядит следующим образом:
- Определить, является ли движение рассматриваемых тел поступательным, ответить на вопрос: «Можно ли принять их за материальные точки?»
- Выбрать инерциальную систему отсчёта. Сделать чертёж с изображением всех сил, действующих на тела, которые участвуют во взаимодействии.
- Записать второй закон Ньютона в векторной форме для каждого тела.
- Записать второй закон Ньютона в проекциях на координатные оси для каждого тела.
- Записать третий закон Ньютона.
- Решить полученную систему алгебраических уравнений.
Пример 1
На горизонтальном полу лифта лежит ящик массой 80 кг. Лифт начинает подниматься на верхний этаж с ускорением 0,2 м/с2. Найти вес ящика при движении лифта.
Решение
1. В результате движения лифта система начнёт поступательное движение, поэтому ящик можно принять за материальную точку.
 Рис. 2. Иллюстрация к примеру 1
Рис. 2. Иллюстрация к примеру 1
2. Пусть ось ОХ направлена вправо, ось
OY — вертикально вверх.
На ящик действуют две силы: сила тяжести и сила реакции опоры. На поверхность со стороны ящика действует только одна
сила — его вес (рис. 2). Так как система движется вверх, вектор ускорения также направлен вертикально вверх.
3. Второй закон Ньютона в векторной форме для ящика имеет следующий вид:
.
4. Запишем второй закон Ньютона в проекциях на координатные оси: в данном случае проекции сил и ускорения на ось ОХ равны нулю, поэтому достаточно записать проекцию на ось ординат:
.
5. В рассматриваемой задаче взаимодействуют ящик и горизонтальная поверхность лифта: ящик действует на поверхность с силой, равной его весу, поверхность — с силой реакции опоры. По третьему закону Ньютона эти силы равны по модулю и противоположны по направлению:
.
6. Решаем систему уравнений:
.
Используя метод подстановки, выражаем искомую силу Р:
.
Ответ: .
Пример 2
Два бруска удерживаются на плоскости, поверхность которой наклонена под углом 60° к горизонту. Масса брусков одинакова и равна 4 кг. Коэффициент трения между первым бруском и поверхностью равен 0,6. Второй брусок гладкий. После того, как бруски отпускают, они приходят в движение. Рассчитайте, с какой силой второй брусок действует на первый в процессе их совместного движения.
Решение
1. После того, как бруски перестают удерживать на наклонной плоскости, они начинают двигаться поступательно, поэтому оба тела можно принять за материальные точки.
 Рис. 3. Иллюстрация к примеру 2
Рис. 3. Иллюстрация к примеру 2
2. В качестве тела отсчёта выберем неподвижную наклонную плоскость. Пусть ось ОХ направлена в сторону движения брусков вдоль поверхности (рис. 3), ось OY — перпендикулярно оси ОХ.
Массы первого и второго брусков обозначим m1 и m2 соответственно. Вектор ускорения направлен в сторону движения брусков. Силы, с которыми взаимодействуют бруски 1 и 2 обозначим как и .
3. Запишем второй закон Ньютона в векторной форме для первого и для второго тела:
;
.
4. Запишем второй закон Ньютона для каждого из тел в проекциях на координатные оси. Учтём, что в выбранной системе отсчёта проекция ускорения на ось ординат равна нулю.
;
;
;
.
Найдём проекции силы тяжести на координатные оси.
5. Согласно третьему закону Ньютона, силы и направлены в противоположные стороны и равны по модулю:
.
6. Известно, что сила трения по определению равна произведению коэффициента трения на силу реакции опоры:
.
Сведём все полученные закономерности в следующую систему уравнений:
.
Используя метод подстановки, выражаем искомую силу F:
.
Ответ: .
Пример 3
 Рис. 4. Иллюстрация к примеру 3
Рис. 4. Иллюстрация к примеру 3
На гладкой горизонтальной поверхности друг на друге лежат два бруска (рис. 4). Коэффициент трения между брусками равен 0,4.
Определите, с какой минимальной силой F надо подействовать на брусок массой m1, чтобы брусок массой m2 начал по нему скользить. Массы брусков равны m1 = 5 кг и m2 = 2 кг.
Решение
1. Пусть бруски двигаются поступательно, поэтому оба тела можно принять за материальные точки.
 Рис. 5. Иллюстрация к примеру 3: силы, действующие на бруски
Рис. 5. Иллюстрация к примеру 3: силы, действующие на бруски
2. В качестве тела отсчёта выберем неподвижную плоскость, на которой лежат бруски. Пусть ось ОХ направлена в сторону движения брусков вдоль поверхности
(рис. 5), ось OY — перпендикулярно оси ОХ. Вектор ускорения направлен в сторону движения брусков. В месте соприкосновения брусков возникают силы трения, препятствующие взаимному движению и .
На брусок массой m1 действуют сила тяжести, сила реакции опоры, сила F, а также сила трения и вес, создаваемый бруском массой m2.
На брусок массой m2 действуют сила тяжести, сила реакции опоры и сила трения, возникающая в процессе взаимного движения.
3. Запишем второй закон Ньютона в векторной форме для первого и для второго тела:
;
.
4. Запишем второй закон Ньютона для каждого из тел в проекциях на координатные оси. Учтём, что в выбранной системе отсчёта проекция ускорения на ось ординат равна нулю:
;
;
;
.
5. Согласно третьему закону Ньютона, силы и направлены в противоположные стороны и равны по модулю:
.
Следует понимать, что в данном случае Fтр1 не зависит от N1, так как данная сила возникает не из-за трения тела m1 о поверхность, а является следствием трения брусков друг о друга, поэтому Fтр1 определяется силой реакции опоры, действующей на верхний брусок N2.
Аналогичные рассуждения применимы к паре сил и , по третьему закону Ньютона эти силы равны по модулю:
.
6. Запишем формулу силы трения:
.
Сведём все полученные соотношения в следующую систему уравнений:
.
Используя метод подстановки, выражаем искомую силу F:
.
Ответ: .
Упражнение 1
1. На горизонтальном полу лифта лежит ящик массой 10 кг. Лифт начинает опускаться на нижний этаж с ускорением 0,4 м/с2. Найти вес ящика в процессе движения лифта.
2. На наклонной плоскости длиной 5 м и высотой 4 м находится груз массой 40 кг. Какую силу, направленную вдоль плоскости, необходимо приложить, чтобы тянуть груз с ускорением 2 м/с2? Коэффициент трения 0,4.
Контрольные вопросы
1. Сформулируйте третий закон Ньютона.
2. На полу лифта на весах находится ящик. Как изменятся показания весов, когда лифт начнёт опускаться на нижний этаж с некоторым ускорением?
3. Как направлена сила трения, если брусок покоится на наклонной плоскости?
Упражнение 1
1. Р = 96 Н
2. F = 496 Н



