- Гравитационные силы. Закон всемирного тяготения
- Ускорение свободного падения
- знать понятие «гравитационные силы»; формулировку закона всемирного тяготения; формулу ускорения свободного падения
- уметь объяснять, от каких величин зависит величина силы притяжения; описывать опыт по измерению гравитационной постоянной; объяснять причины, по которым ускорение свободного падения имеет различные значения в разных точках земного шара
- Действие какой силы обуславливает движение Земли вокруг Солнца?
- Дайте определение силы тяжести.
- Что такое ускорение свободного падения?
Гравитационные силы. Закон Всемирного тяготения
Известно, что Земля притягивает к себе все тела, находящиеся на её поверхности с силой тяжести . Согласно третьему закону Ньютона, тело, в свою очередь, тоже будет притягивать к себе Землю с силой, равной по модулю силе тяжести . Исаак Ньютон предположил, что силы притяжения существуют между всеми телами во Вселенной.
Все тела во Вселенной притягиваются друг к другу с силами, которые называются силами всемирного тяготения или гравитационными силами.
Из известной нам формулы силы тяжести очевидно, что модуль силы тяжести Fт, действующей на некоторое тело, всегда пропорционален массе тела m. С другой стороны, тело тоже притягивает Землю с силой, равной по модулю силе тяжести, тогда модуль этой силы F должен быть пропорционален массе Земли MЗ. Получается, что сила гравитационного взаимодействия двух тел прямо пропорциональна величине .
Чтобы определить зависимость силы тяготения от расстояния между телами, Ньютон исследовал движение Луны. Учёный предположил, что Луна движется вокруг Земли под действием гравитационной силы Земли. Результатом действия гравитационной силы как для подброшенного в воздух камня, так и для Луны, является возникновение ускорения. Но камень падает на Землю, а Луна вращается вокруг Земли по своей орбите, следовательно, ускорения, приобретённые телами в результате действия гравитационной силы, различны. Логично предположить, что эти различия объясняются совершенно разными расстояниями между Землёй и камнем, между Землёй и Луной.
Камень, подброшенный вверх, будет падать с ускорением свободного падения, равным по модулю g = 9,8 м/с2.
Ускорение Луны было рассчитано Ньютоном, благодаря хорошо изученной на тот момент траектории её движения. Ускорение Луны составляет примерно aцс = 0,0027 м/с2, что меньше значения g примерно в 3 600 раз.
Расстояние от центра Земли до её поверхности примерно в 60 раз меньше расстояния между центром Земли и Луной.
Таким образом, увеличение расстояния между взаимодействующими телами в 60 раз приводит к уменьшению сообщаемого ускорения в 3 600 раз. На основании этих данных Ньютон предположил, что модуль силы гравитационного взаимодействия обратно пропорционален квадрату расстояния между телами.
Таким образом, сила тяготения между Землёй и некоторым телом на её поверхности прямо пропорциональна произведению массы тела и массы планеты и обратно пропорциональна квадрату расстояния между телом и центром Земли:
.
Исследование характера движения планет вокруг Солнца позволило Ньютону выявить аналогичную зависимость для силы притяжения между Солнцем и движущимися вокруг него планетами: сила тяготения между Солнцем и планетой прямо пропорциональна произведению массы Солнца и массы планеты и обратно пропорциональна квадрату расстояния между ними:
.
Полученная закономерность подтвердила предположение учёного, что силы тяготения испытывают на себе все тела во Вселенной.
На основании приведённых расчётов в 1687 г. Ньютон сформулировал закон всемирного тяготения:
, где
— сила тяготения между двумя телами;
— гравитационная постоянная;
и — массы первого и второго тела соответственно;
— расстояние между телами.
Закон всемирного тяготения: две материальные точки массами m1 и m2 притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними: .
Гравитационная постоянная G — это коэффициент, одинаковый для любой пары взаимодействующих тел.
Закон всемирного тяготения применим только к телам, расстояние между которыми во много раз больше размеров самих тел.
Для тел, имеющих форму шара, величина R соответствует расстоянию между центрами данных шаров. Для тел иной формы закон всемирного тяготения также применим, но требует более сложных математических расчётов.
Более чем через сто лет после открытия Ньютоном закона всемирного тяготения английский физик Генри Кавендиш смог экспериментально измерить значение гравитационной постоянной G. Для этого учёный использовал крутильные весы, знакомые нам по экспериментам Кулона (рис. 1).
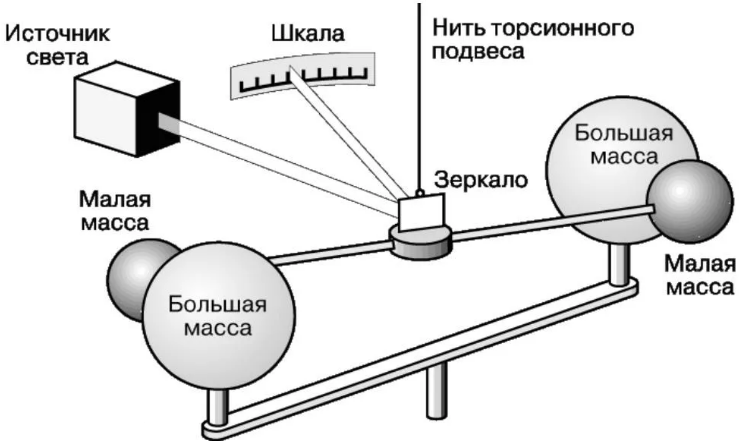 Рис. 1. Опыт Кавендиша по определению гравитационной постоянной
Рис. 1. Опыт Кавендиша по определению гравитационной постоянной
На лёгком стержне (коромысле) были закреплены два маленьких свинцовых шарика массами m. Вблизи были закреплены два тяжёлых шара массами M. В результате взаимного притяжения стержень двигался на нити, на которой было закреплено небольшое зеркальце. Отражённый от зеркальца луч попадал на шкалу, которая позволяла определить угол поворота.
Ускорение свободного падения
Если применить закон всемирного тяготения к Земле и телу массой m, формула будет иметь следующий вид:
,
где — масса тела у поверхности Земли;
— масса Земли;
— средний радиус Земли.
Сравним полученное выражение с формулой силы тяжести:
.
Глядя на формулы нетрудно заметить, что ускорение свободного падения представляет собой множитель в законе всемирного тяготения, находящийся возле массы тела:
.
Таким образом, ускорение свободного падения на поверхности любой планеты можно найти как произведение гравитационной постоянной и массы:
.
Ускорение свободного падения на поверхности планеты рассчитывается по следующей формуле: .
Формула выше позволяет объяснить, почему в разных точках планеты ускорение свободного падения имеет разное значение. Так, ускорение свободного падения на экваторе Земли меньше, чем на полюсах, потому что наша планета имеет форму немного сплюснутого у полюсов шара.
 Рис. 2. Модуль ускорения свободного падения Земли зависит от широты
Рис. 2. Модуль ускорения свободного падения Земли зависит от широты
Ещё одна причина меньшего значения ускорения у полюсов — вращение Земли вокруг своей оси. Все тела, находящиеся на поверхности Земли, вследствие этого вращения движутся по окружностям разного радиуса.
Пусть на земном экваторе тело движется по окружности радиуса R. Тогда тело, расположенное на широте , движется по окружности радиуса (рис. 2).
Тогда тело, расположенное на широте , обладает центростремительным ускорением. Следовательно, ускорение данного тела складывается из ускорения свободного падения на экваторе и центростремительного ускорения. Таким образом, модуль ускорения свободного падения Земли зависит от широты.
Итоги
- Все тела во Вселенной притягиваются друг к другу с силами, которые называются силами всемирного тяготения или гравитационными силами.
- Закон всемирного тяготения: две материальные точки массами m1 и m2 притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними: .
- — гравитационная постоянная.
- Ускорение свободного падения на поверхности планеты рассчитывается по следующей формуле: .
Контрольные вопросы
1. Сформулируйте закон всемирного тяготения.
2. Используя рисунок 1, опишите опыт Кавендиша по определению значения гравитационной постоянной.
3. По какой формуле рассчитывается ускорение свободного падения?
- Гравитационные силы. Закон всемирного тяготения
- Ускорение свободного падения
- знать понятие «гравитационные силы»; формулировку закона всемирного тяготения; формулу ускорения свободного падения
- уметь объяснять, от каких величин зависит величина силы притяжения; описывать опыт по измерению гравитационной постоянной; объяснять причины, по которым ускорение свободного падения имеет различные значения в разных точках земного шара
- Действие какой силы обуславливает движение Земли вокруг Солнца?
- Дайте определение силы тяжести.
- Что такое ускорение свободного падения?
Гравитационные силы. Закон Всемирного тяготения
Известно, что Земля притягивает к себе все тела, находящиеся на её поверхности с силой тяжести . Согласно третьему закону Ньютона, тело, в свою очередь, тоже будет притягивать к себе Землю с силой, равной по модулю силе тяжести . Исаак Ньютон предположил, что силы притяжения существуют между всеми телами во Вселенной.
Все тела во Вселенной притягиваются друг к другу с силами, которые называются силами всемирного тяготения или гравитационными силами.
Из известной нам формулы силы тяжести очевидно, что модуль силы тяжести Fт, действующей на некоторое тело, всегда пропорционален массе тела m. С другой стороны, тело тоже притягивает Землю с силой, равной по модулю силе тяжести, тогда модуль этой силы F должен быть пропорционален массе Земли MЗ. Получается, что сила гравитационного взаимодействия двух тел прямо пропорциональна величине .
Чтобы определить зависимость силы тяготения от расстояния между телами, Ньютон исследовал движение Луны. Учёный предположил, что Луна движется вокруг Земли под действием гравитационной силы Земли. Результатом действия гравитационной силы как для подброшенного в воздух камня, так и для Луны, является возникновение ускорения. Но камень падает на Землю, а Луна вращается вокруг Земли по своей орбите, следовательно, ускорения, приобретённые телами в результате действия гравитационной силы, различны. Логично предположить, что эти различия объясняются совершенно разными расстояниями между Землёй и камнем, между Землёй и Луной.
Камень, подброшенный вверх, будет падать с ускорением свободного падения, равным по модулю g = 9,8 м/с2.
Ускорение Луны было рассчитано Ньютоном, благодаря хорошо изученной на тот момент траектории её движения. Ускорение Луны составляет примерно aцс = 0,0027 м/с2, что меньше значения g примерно в 3 600 раз.
Расстояние от центра Земли до её поверхности примерно в 60 раз меньше расстояния между центром Земли и Луной.
Таким образом, увеличение расстояния между взаимодействующими телами в 60 раз приводит к уменьшению сообщаемого ускорения в 3 600 раз. На основании этих данных Ньютон предположил, что модуль силы гравитационного взаимодействия обратно пропорционален квадрату расстояния между телами.
Таким образом, сила тяготения между Землёй и некоторым телом на её поверхности прямо пропорциональна произведению массы тела и массы планеты и обратно пропорциональна квадрату расстояния между телом и центром Земли:
.
Исследование характера движения планет вокруг Солнца позволило Ньютону выявить аналогичную зависимость для силы притяжения между Солнцем и движущимися вокруг него планетами: сила тяготения между Солнцем и планетой прямо пропорциональна произведению массы Солнца и массы планеты и обратно пропорциональна квадрату расстояния между ними:
.
Полученная закономерность подтвердила предположение учёного, что силы тяготения испытывают на себе все тела во Вселенной.
На основании приведённых расчётов в 1687 г. Ньютон сформулировал закон всемирного тяготения:
, где
— сила тяготения между двумя телами;
— гравитационная постоянная;
и — массы первого и второго тела соответственно;
— расстояние между телами.
Закон всемирного тяготения: две материальные точки массами m1 и m2 притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними: .
Гравитационная постоянная G — это коэффициент, одинаковый для любой пары взаимодействующих тел.
Закон всемирного тяготения применим только к телам, расстояние между которыми во много раз больше размеров самих тел.
Для тел, имеющих форму шара, величина R соответствует расстоянию между центрами данных шаров. Для тел иной формы закон всемирного тяготения также применим, но требует более сложных математических расчётов.
Более чем через сто лет после открытия Ньютоном закона всемирного тяготения английский физик Генри Кавендиш смог экспериментально измерить значение гравитационной постоянной G. Для этого учёный использовал крутильные весы, знакомые нам по экспериментам Кулона (рис. 1).
 Рис. 1. Опыт Кавендиша по определению гравитационной постоянной
Рис. 1. Опыт Кавендиша по определению гравитационной постоянной
На лёгком стержне (коромысле) были закреплены два маленьких свинцовых шарика массами m. Вблизи были закреплены два тяжёлых шара массами M. В результате взаимного притяжения стержень двигался на нити, на которой было закреплено небольшое зеркальце. Отражённый от зеркальца луч попадал на шкалу, которая позволяла определить угол поворота.
Ускорение свободного падения
Если применить закон всемирного тяготения к Земле и телу массой m, формула будет иметь следующий вид:
,
где — масса тела у поверхности Земли;
— масса Земли;
— средний радиус Земли.
Сравним полученное выражение с формулой силы тяжести:
.
Глядя на формулы нетрудно заметить, что ускорение свободного падения представляет собой множитель в законе всемирного тяготения, находящийся возле массы тела:
.
Таким образом, ускорение свободного падения на поверхности любой планеты можно найти как произведение гравитационной постоянной и массы:
.
Ускорение свободного падения на поверхности планеты рассчитывается по следующей формуле: .
Формула выше позволяет объяснить, почему в разных точках планеты ускорение свободного падения имеет разное значение. Так, ускорение свободного падения на экваторе Земли меньше, чем на полюсах, потому что наша планета имеет форму немного сплюснутого у полюсов шара.
 Рис. 2. Модуль ускорения свободного падения Земли зависит от широты
Рис. 2. Модуль ускорения свободного падения Земли зависит от широты
Ещё одна причина меньшего значения ускорения у полюсов — вращение Земли вокруг своей оси. Все тела, находящиеся на поверхности Земли, вследствие этого вращения движутся по окружностям разного радиуса.
Пусть на земном экваторе тело движется по окружности радиуса R. Тогда тело, расположенное на широте , движется по окружности радиуса (рис. 2).
Тогда тело, расположенное на широте , обладает центростремительным ускорением. Следовательно, ускорение данного тела складывается из ускорения свободного падения на экваторе и центростремительного ускорения. Таким образом, модуль ускорения свободного падения Земли зависит от широты.
Итоги
- Все тела во Вселенной притягиваются друг к другу с силами, которые называются силами всемирного тяготения или гравитационными силами.
- Закон всемирного тяготения: две материальные точки массами m1 и m2 притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними: .
- — гравитационная постоянная.
- Ускорение свободного падения на поверхности планеты рассчитывается по следующей формуле: .
Контрольные вопросы
1. Сформулируйте закон всемирного тяготения.
2. Используя рисунок 1, опишите опыт Кавендиша по определению значения гравитационной постоянной.
3. По какой формуле рассчитывается ускорение свободного падения?



