- Второй закон Ньютона
- Примеры решения задач
- знать формулировку второго закона Ньютона
- уметь решать задачи на движение тела под действием нескольких сил
- Что такое инерциальная система отсчёта?
- Как найти равнодействующую силу?
- Как направлена сила трения, сила реакции опоры?
Второй закон Ньютона
Результатом действия равнодействующей силы на тело является приобретение телом ускорения. При этом модуль ускорения тела равен отношению модуля равнодействующей силы к массе данного тела:
,
где [м/с2] — ускорение тела;
[Н] — равнодействующая всех сил, действующих на тело;
[кг] — масса тела.
Ускорение тела направлено в ту же сторону, куда и равнодействующая сила. Соотношение выше называется вторым законом Ньютона.
Второй закон Ньютона: в инерциальной системе отсчёта ускорение, приобретённое телом в результате действия силы или нескольких сил, прямо пропорционально равнодействующей силе и обратно пропорционально массе этого тела: .
При известном ускорении и массе тела выражение выше позволяет найти модуль равнодействующей силы:
.
Формулы выше записаны через модули ускорения и равнодействующей силы. Понятно, что также справедлива будет запись в проекциях на оси ОХ и OY:
;
.
Таким образом, в инерциальной системе отсчета произведение массы тела на проекцию ускорения на координатную ось равно сумме проекций всех сил, действующих на тело, на выбранную ось:
;
.
Соотношения выше показывают, что в инерциальной системе отсчёта проекция ускорения материальной точки на выбранную координатную ось не зависит от проекций сил, действующих на данное тело, на другие координатные оси.
Примеры решения задач
Решение задач о движении тела под действием нескольких сил можно представить в виде следующего алгоритма:
- Определить, является ли движение рассматриваемого тела поступательным, ответить на вопрос: «Можно ли принять его за материальную точку?»
- Выбрать инерциальную систему отсчёта. Сделать чертеж с изображением всех сил, действующих на тело.
- Записать второй закон Ньютона в векторной форме.
- Записать второй закон Ньютона в проекциях на координатные оси.
- Решить систему уравнений и выразить неизвестную величину.
- Произвести численный расчёт.
Отметим, что, если в задаче говорится о том, что поверхность, по которой движется тело, «гладкая», в этом случае силой трения скольжения необходимо пренебречь.
Пример 1
На горизонтальном полу лежит ящик массой 10 кг. Коэффициент трения между ящиком и полом равен 0,4. К ящику в горизонтальном направлении прикладывают силу F, в результате чего ящик начинает двигаться с ускорением 0,2 м/с2. Найти значение силы, приложенной к телу.
Решение
1. В результате действия силы F ящик начнёт поступательное движение, поэтому его можно принять за материальную точку.
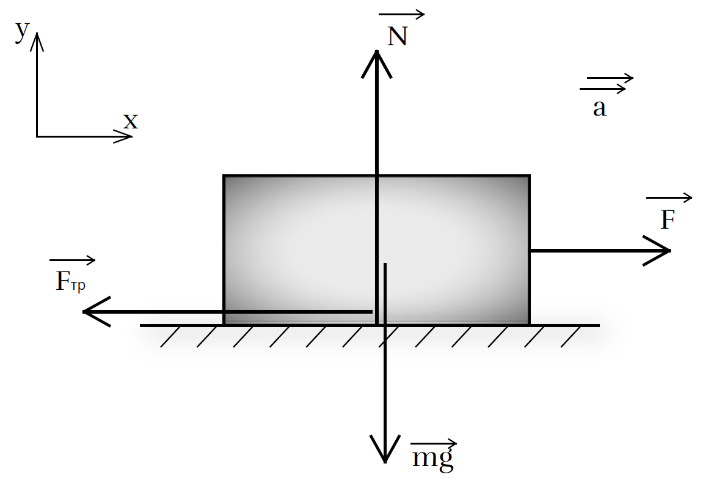 Рис. 1. Иллюстрация к примеру 1
Рис. 1. Иллюстрация к примеру 1
2. В качестве тела отсчёта выберем поверхность неподвижного стола. Пусть ось ОХ направлена в сторону действия силы
F — вправо (рис. 1), ось
OY — вертикально вверх.
На тело действуют четыре силы: сила тяжести, сила трения, сила реакции опоры и сила тяги F. Так как по условию задачи тело пришло в движение, равнодействующая сил направлена в сторону действия силы F, по второму закону Ньютона ускорение направлено в ту же сторону, что и равнодействующая: в нашем случае — вправо.
3. Запишем второй закон Ньютона в векторной форме:
.
4. Запишем второй закон Ньютона в проекциях на координатные оси:
;
.
Так как ускорение тела направлено перпендикулярно оси OY, проекция ускорения на данную ось равна нулю.
5. Решаем систему уравнений относительно неизвестной силы F. Известно, что сила трения скольжения по определению равна произведению коэффициента трения на силу реакции опоры:
.
Учитывая эту формулу, получаем следующую систему уравнений:
Используя метод подстановки, выражаем искомую силу F:
.
Ответ: .
Пример 2
Спиленное дерево массой 80 кг с помощью лебёдки равноускоренно втаскивается на наклонную поверхность грузовой платформы трактора. Угол наклона платформы составляет 30°. Динамометр, контролирующий натяжение троса лебёдки, показывает силу 1 000 Н. Определите коэффициент трения скольжения между бревном и платформой, если ускорение бревна равно 2 м/с2.
Решение
1. В результате действия силы тяги бревно двигается поступательно, поэтому его можно принять за материальную точку.
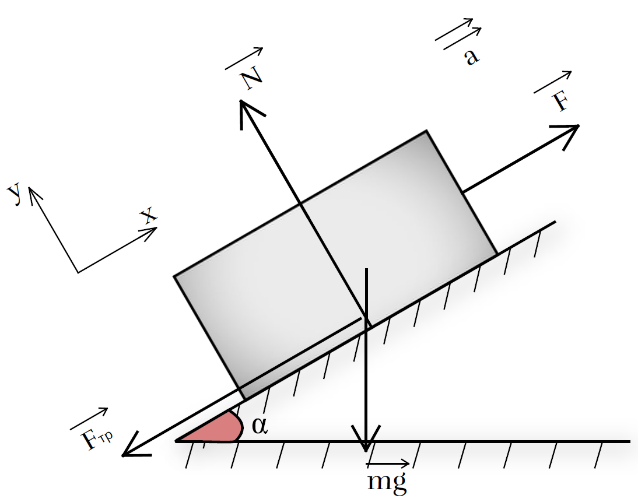 Рис. 2. Иллюстрация к примеру 2
Рис. 2. Иллюстрация к примеру 2
2. В качестве тела отсчёта выберем поверхность неподвижной платформы. Пусть ось ОХ направлена в сторону действия силы тяги F вдоль поверхности платформы (рис. 2), ось
OY — перпендикулярно оси ОХ. На тело действуют четыре силы: сила тяжести, сила трения, сила реакции опоры и сила тяги F. Так как по условию задачи тело движется вверх по платформе, равнодействующая сил направлена в сторону действия силы F, по второму закону Ньютона ускорение направлено в ту же сторону, что и равнодействующая.
3. Запишем второй закон Ньютона в векторной форме:
.
4. Запишем второй закон Ньютона в проекциях на координатные оси:
;
.
Так как ускорение тела направлено перпендикулярно оси OY, проекция ускорения на данную ось равна нулю.
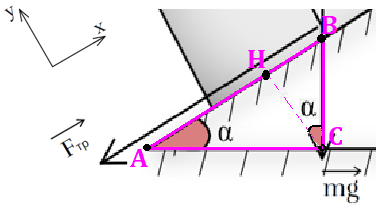 Рис. 3. Определения проекции силы тяжести на координатные оси
Рис. 3. Определения проекции силы тяжести на координатные оси
Найдём проекцию силы тяжести на ось ОХ. Пусть вектор соответствует вектору (рис. 3). Опустим перпендикуляр из точки С на ось ОХ, тогда проекция силы тяжести на данную ось равна отрезку ВН: . Рассмотрим треугольники АВС и СВН, они подобны, следовательно, угол ВАС равен углу ВСН: .
В треугольнике ВСН: , тогда
.
Аналогично определяем проекцию силы тяжести на ось OY:
.
5. Известно, что сила трения скольжения по определению равна произведению коэффициента трения на силу реакции опоры:
.
Учитывая формулы выше, получаем следующую систему уравнений:
Используя метод подстановки, выражаем искомый коэффициент трения :
.
Ответ: .
Упражнение 1
1. На горизонтальном полу лежит брусок массой 5 кг. Коэффициент трения между ящиком и полом равен 0,3. К ящику в горизонтальном направлении прикладывают силу F, в результате чего ящик начинает двигаться с ускорением 0,1 м/с2. Найти значение силы, приложенной к телу.
2. Шарик катится вверх по гладкой наклонной плоскости, составляющей угол 45° с горизонтом. Определите начальную скорость шарика, если до полной остановки он прошёл 50 см.
3. Брусок массой 100 г покоится на наклонной плоскости. Определите коэффициент трения между бруском и поверхностью, если угол наклона плоскости к горизонту равен 30°.
Контрольные вопросы
1. Сформулируйте второй закон Ньютона.
2. Чему равна равнодействующая сил, действующих на тело, если оно движется равномерно?
3. Как направлена равнодействующая тела, движущегося по окружности?
Упражнение 1
1. = 15,5 Н
2.
3. = 0,6
- Второй закон Ньютона
- Примеры решения задач
- знать формулировку второго закона Ньютона
- уметь решать задачи на движение тела под действием нескольких сил
- Что такое инерциальная система отсчёта?
- Как найти равнодействующую силу?
- Как направлена сила трения, сила реакции опоры?
Второй закон Ньютона
Результатом действия равнодействующей силы на тело является приобретение телом ускорения. При этом модуль ускорения тела равен отношению модуля равнодействующей силы к массе данного тела:
,
где [м/с2] — ускорение тела;
[Н] — равнодействующая всех сил, действующих на тело;
[кг] — масса тела.
Ускорение тела направлено в ту же сторону, куда и равнодействующая сила. Соотношение выше называется вторым законом Ньютона.
Второй закон Ньютона: в инерциальной системе отсчёта ускорение, приобретённое телом в результате действия силы или нескольких сил, прямо пропорционально равнодействующей силе и обратно пропорционально массе этого тела: .
При известном ускорении и массе тела выражение выше позволяет найти модуль равнодействующей силы:
.
Формулы выше записаны через модули ускорения и равнодействующей силы. Понятно, что также справедлива будет запись в проекциях на оси ОХ и OY:
;
.
Таким образом, в инерциальной системе отсчета произведение массы тела на проекцию ускорения на координатную ось равно сумме проекций всех сил, действующих на тело, на выбранную ось:
;
.
Соотношения выше показывают, что в инерциальной системе отсчёта проекция ускорения материальной точки на выбранную координатную ось не зависит от проекций сил, действующих на данное тело, на другие координатные оси.
Примеры решения задач
Решение задач о движении тела под действием нескольких сил можно представить в виде следующего алгоритма:
- Определить, является ли движение рассматриваемого тела поступательным, ответить на вопрос: «Можно ли принять его за материальную точку?»
- Выбрать инерциальную систему отсчёта. Сделать чертеж с изображением всех сил, действующих на тело.
- Записать второй закон Ньютона в векторной форме.
- Записать второй закон Ньютона в проекциях на координатные оси.
- Решить систему уравнений и выразить неизвестную величину.
- Произвести численный расчёт.
Отметим, что, если в задаче говорится о том, что поверхность, по которой движется тело, «гладкая», в этом случае силой трения скольжения необходимо пренебречь.
Пример 1
На горизонтальном полу лежит ящик массой 10 кг. Коэффициент трения между ящиком и полом равен 0,4. К ящику в горизонтальном направлении прикладывают силу F, в результате чего ящик начинает двигаться с ускорением 0,2 м/с2. Найти значение силы, приложенной к телу.
Решение
1. В результате действия силы F ящик начнёт поступательное движение, поэтому его можно принять за материальную точку.
 Рис. 1. Иллюстрация к примеру 1
Рис. 1. Иллюстрация к примеру 1
2. В качестве тела отсчёта выберем поверхность неподвижного стола. Пусть ось ОХ направлена в сторону действия силы
F — вправо (рис. 1), ось
OY — вертикально вверх.
На тело действуют четыре силы: сила тяжести, сила трения, сила реакции опоры и сила тяги F. Так как по условию задачи тело пришло в движение, равнодействующая сил направлена в сторону действия силы F, по второму закону Ньютона ускорение направлено в ту же сторону, что и равнодействующая: в нашем случае — вправо.
3. Запишем второй закон Ньютона в векторной форме:
.
4. Запишем второй закон Ньютона в проекциях на координатные оси:
;
.
Так как ускорение тела направлено перпендикулярно оси OY, проекция ускорения на данную ось равна нулю.
5. Решаем систему уравнений относительно неизвестной силы F. Известно, что сила трения скольжения по определению равна произведению коэффициента трения на силу реакции опоры:
.
Учитывая эту формулу, получаем следующую систему уравнений:
Используя метод подстановки, выражаем искомую силу F:
.
Ответ: .
Пример 2
Спиленное дерево массой 80 кг с помощью лебёдки равноускоренно втаскивается на наклонную поверхность грузовой платформы трактора. Угол наклона платформы составляет 30°. Динамометр, контролирующий натяжение троса лебёдки, показывает силу 1 000 Н. Определите коэффициент трения скольжения между бревном и платформой, если ускорение бревна равно 2 м/с2.
Решение
1. В результате действия силы тяги бревно двигается поступательно, поэтому его можно принять за материальную точку.
 Рис. 2. Иллюстрация к примеру 2
Рис. 2. Иллюстрация к примеру 2
2. В качестве тела отсчёта выберем поверхность неподвижной платформы. Пусть ось ОХ направлена в сторону действия силы тяги F вдоль поверхности платформы (рис. 2), ось
OY — перпендикулярно оси ОХ. На тело действуют четыре силы: сила тяжести, сила трения, сила реакции опоры и сила тяги F. Так как по условию задачи тело движется вверх по платформе, равнодействующая сил направлена в сторону действия силы F, по второму закону Ньютона ускорение направлено в ту же сторону, что и равнодействующая.
3. Запишем второй закон Ньютона в векторной форме:
.
4. Запишем второй закон Ньютона в проекциях на координатные оси:
;
.
Так как ускорение тела направлено перпендикулярно оси OY, проекция ускорения на данную ось равна нулю.
 Рис. 3. Определения проекции силы тяжести на координатные оси
Рис. 3. Определения проекции силы тяжести на координатные оси
Найдём проекцию силы тяжести на ось ОХ. Пусть вектор соответствует вектору (рис. 3). Опустим перпендикуляр из точки С на ось ОХ, тогда проекция силы тяжести на данную ось равна отрезку ВН: . Рассмотрим треугольники АВС и СВН, они подобны, следовательно, угол ВАС равен углу ВСН: .
В треугольнике ВСН: , тогда
.
Аналогично определяем проекцию силы тяжести на ось OY:
.
5. Известно, что сила трения скольжения по определению равна произведению коэффициента трения на силу реакции опоры:
.
Учитывая формулы выше, получаем следующую систему уравнений:
Используя метод подстановки, выражаем искомый коэффициент трения :
.
Ответ: .
Упражнение 1
1. На горизонтальном полу лежит брусок массой 5 кг. Коэффициент трения между ящиком и полом равен 0,3. К ящику в горизонтальном направлении прикладывают силу F, в результате чего ящик начинает двигаться с ускорением 0,1 м/с2. Найти значение силы, приложенной к телу.
2. Шарик катится вверх по гладкой наклонной плоскости, составляющей угол 45° с горизонтом. Определите начальную скорость шарика, если до полной остановки он прошёл 50 см.
3. Брусок массой 100 г покоится на наклонной плоскости. Определите коэффициент трения между бруском и поверхностью, если угол наклона плоскости к горизонту равен 30°.
Контрольные вопросы
1. Сформулируйте второй закон Ньютона.
2. Чему равна равнодействующая сил, действующих на тело, если оно движется равномерно?
3. Как направлена равнодействующая тела, движущегося по окружности?
Упражнение 1
1. = 15,5 Н
2.
3. = 0,6



