- Сила натяжения нити
- Примеры решения задач
- знать алгоритм решения задач о движении связанных тел
- уметь применять второй и третий законы Ньютона для решения задач на движение связанных тел
- Сформулируйте третий закон Ньютона.
- В каких случаях возникает сила упругости?
- Куда направлена сила упругости?
Сила натяжения нити
Решение задач о движении связанных тел осуществляется по уже изученному нами алгоритму.
В данном блоке задач особое внимание следует уделить силам упругости, возникающим в нити при движении связанных тел. Вспомним, что сила упругости, появляющаяся в нерастяжимой нити, называется силой натяжения нити и обозначается .
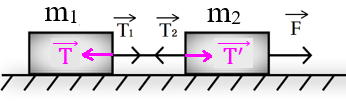 Рис. 1. Силы, возникающие в системе из двух брусков, связанных нитью, в результате действия силы F
Рис. 1. Силы, возникающие в системе из двух брусков, связанных нитью, в результате действия силы F
Рассмотрим, какие силы возникают в системе из двух брусков, связанных невесомой нитью, если на один из них подействовать с некоторой силой F (рис. 1).
В результате действия силы F брусок 2 приходит в движение, нить, связывающая бруски, начинает действовать на брусок 1 с силой . По третьему закону Ньютона брусок действует на нить с силой такой, что .
Аналогичные рассуждения применимы ко второму бруску: нить действует на него с силой , брусок действует на нить с такой силой , что .
Таким образом, силы и действуют на нить, а силы и — на связанные бруски.
Если натянутая нить невесома, силы упругости, возникающие в различных частях нити, равны по модулю:
.
Так как и , справедливо будет записать следующее равенство:
.
При решении задач может быть нецелесообразно рисовать силы и , возникающие в нити, за исключением случая, когда нить обладает массой и данные силы не равны друг другу (решение подобной задачи рассмотрено в примере 3).
Примеры решения задач
Пример 1
Два бруска массами m1 = 2 кг и m2 = 6 кг связаны лёгкой невесомой нерастяжимой нитью. В некоторый момент времени на брусок массой m2 начинает действовать сила F = 10 Н, в результате чего бруски начинают поступательное движение. Найти ускорение системы брусков. Поверхность и бруски считать гладкими.
Решение
1. После того как на второй брусок начинает действовать сила F, система начинает двигаться поступательно, поэтому оба тела можно принять за материальные точки.
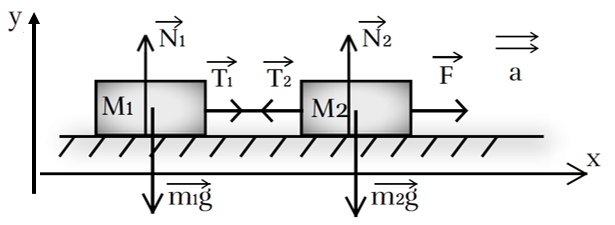 Рис. 2. Иллюстрация к примеру 1
Рис. 2. Иллюстрация к примеру 1
2. В качестве тела отсчёта выберем неподвижную плоскость, по которой движутся бруски. Пусть ось ОХ направлена в сторону движения брусков: так как сила F направлена вправо, система будет двигаться в направлении данной силы (рис. 2). Ось OY направлена перпендикулярно оси ОХ.
Изобразим силы, действующие на бруски. Силы упругости, возникающие в нити, изображать не обязательно, так как в данном случае мы не будем применять второй закон Ньютона к нити, связывающей тела.
3. Поскольку нить нерастяжима, то ускорение связанных тел будет одинаково. Запишем второй закон Ньютона в векторной форме для первого и для второго бруска:
;
.
4. Запишем второй закон Ньютона для каждого из тел в проекциях на координатные оси:
;
;
;
;
5. Как мы уже знаем, при движении связанных невесомой нитью тел силы натяжения нити Т1 и Т2, приложенные к телам, равны по модулю:
.
6. Обратим внимание, что для решения поставленной задачи достаточно решить систему из уравнений на ось OX.
Решаем полученную систему относительно неизвестного ускорения методом сложения:
Тогда
.
Ответ: .
Пример 2
Через неподвижный невесомый блок перекинута лёгкая нерастяжимая нить. К концам нити прикрепляют грузы массами m1 = 5 кг и m2 = 10 кг, затем их одновременно отпускают. Найти ускорение системы грузов.
Решение
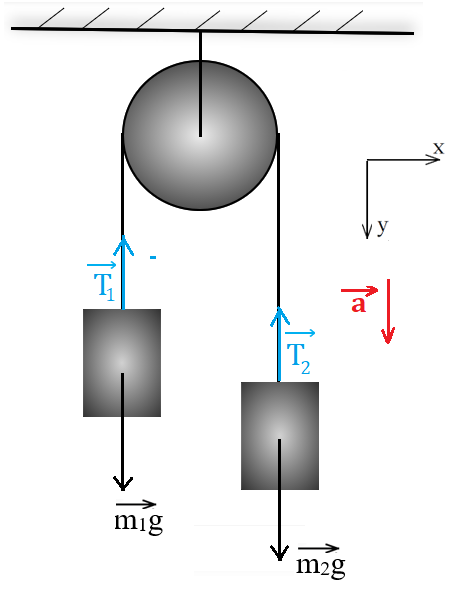 Рис. 3. Иллюстрация к примеру 2
Рис. 3. Иллюстрация к примеру 2
1. После того как грузы отпускают, они начинают двигаться поступательно, поэтому оба тела можно принять за материальные точки.
2. В качестве тела отсчёта выберем неподвижную плоскость, к которой прикреплён блок. Пусть ось ОY направлена в сторону движения брусков: так как брусок массой m2 тяжелее, система будет двигаться в направлении силы (рис. 3).
Ось OХ направлена перпендикулярно оси ОY.
3. Поскольку нить нерастяжима, то ускорение связанных тел будет одинаково. Запишем второй закон Ньютона в векторной форме для первого и для второго тела:
;
.
4. Запишем второй закон Ньютона для каждого из тел в проекциях на координатные оси. Учтём, что в выбранной системе отсчёта проекции ускорения и сил на ось абсцисс равны нулю, поэтому проекции на данную ось можно не рассматривать.
Так как первое тело движется вверх, проекция ускорения данного тела на ось ординат будет отрицательна.
;
.
5. Как мы уже знаем, при движении тел, связанных невесомой нитью, силы натяжения нити Т1 и Т2, приложенные к телам, равны по модулю:
.
6. Решаем полученную систему относительно неизвестного ускорения методом сложения:
Тогда
.
Ответ: .
Пример 3
К одному концу нерастяжимой верёвки массой 0,5 кг привязывают груз массой 2 кг. Верёвку вместе с грузом поднимают вертикально вверх, прикладывая силу, равную 50 Н. Найти ускорение системы, а также модули сил упругости, действующие на противоположные концы верёвки.
Решение
1. Верёвка по условию задачи нерастяжима, примем, что груз и верёвка движутся поступательно, поэтому оба тела можно принять за материальные точки.
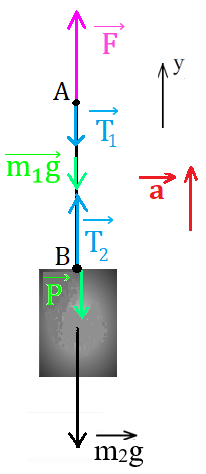 Рис. 4. Иллюстрация к примеру 3: силы, действующие на бруски
Рис. 4. Иллюстрация к примеру 3: силы, действующие на бруски
2. В качестве тела отсчёта выберем поверхность Земли. Ось ОY направим в сторону движения
системы — в направлении действия силы (рис. 4). Обозначим массу груза m2, массу верёвки m1.
К верхнему концу верёвки, к точке А, по условию приложена сила , в этой точке возникает сила упругости , действующая на источник силы (например, на руку человека, который тянет верёвку).
В месте крепления груза, в точке В, на верёвку действует вес груза , в результате в этой точке возникает сила упругости , действующая на груз.
3. Запишем второй закон Ньютона в векторной форме для верёвки и для груза:
;
.
4. Запишем второй закон Ньютона для каждого из тел в проекциях на ось ординат:
;
.
5. По третьему закону Ньютона силы и равны по модулю и противоположны по направлению:
.
6. Решаем полученную систему с учётом соотношения:
Тогда
.
Найдём Т2:
.
Наконец, найдём значение силы Т1: согласно третьему закону Ньютона, данная сила будет равна по модулю и противоположна по направлению силе, с которой верёвку тянут вверх:
.
Ответ: ; ; .
Упражнение 1
1. Два бруска массами m1 = 1 кг и m2 = 3 кг связаны лёгкой невесомой нерастяжимой нитью. В некоторый момент времени на брусок массой m2 начинает действовать сила F = 20 Н, в результате чего бруски начинают поступательное движение. Найти ускорение системы брусков, если коэффициент трения между поверхностью и брусками равен 0,4.
2. На нерастяжимой невесомой нити, перекинутой через неподвижный блок, подвешены грузы массами 300 и 500 г. Какова сила натяжения нити во время движения?
3. Тепловоз массой 80 т тянет два вагона массой по 20 т каждый с ускорением 0,2 м/с2. Найти силу тяги тепловоза, если коэффициент трения равен 0,005.
Упражнение 1
1. а = 1 м/с2
2. T = 3,75 Н
3. F = 30 кН
- Сила натяжения нити
- Примеры решения задач
- знать алгоритм решения задач о движении связанных тел
- уметь применять второй и третий законы Ньютона для решения задач на движение связанных тел
- Сформулируйте третий закон Ньютона.
- В каких случаях возникает сила упругости?
- Куда направлена сила упругости?
Сила натяжения нити
Решение задач о движении связанных тел осуществляется по уже изученному нами алгоритму.
В данном блоке задач особое внимание следует уделить силам упругости, возникающим в нити при движении связанных тел. Вспомним, что сила упругости, появляющаяся в нерастяжимой нити, называется силой натяжения нити и обозначается .
 Рис. 1. Силы, возникающие в системе из двух брусков, связанных нитью, в результате действия силы F
Рис. 1. Силы, возникающие в системе из двух брусков, связанных нитью, в результате действия силы F
Рассмотрим, какие силы возникают в системе из двух брусков, связанных невесомой нитью, если на один из них подействовать с некоторой силой F (рис. 1).
В результате действия силы F брусок 2 приходит в движение, нить, связывающая бруски, начинает действовать на брусок 1 с силой . По третьему закону Ньютона брусок действует на нить с силой такой, что .
Аналогичные рассуждения применимы ко второму бруску: нить действует на него с силой , брусок действует на нить с такой силой , что .
Таким образом, силы и действуют на нить, а силы и — на связанные бруски.
Если натянутая нить невесома, силы упругости, возникающие в различных частях нити, равны по модулю:
.
Так как и , справедливо будет записать следующее равенство:
.
При решении задач может быть нецелесообразно рисовать силы и , возникающие в нити, за исключением случая, когда нить обладает массой и данные силы не равны друг другу (решение подобной задачи рассмотрено в примере 3).
Примеры решения задач
Пример 1
Два бруска массами m1 = 2 кг и m2 = 6 кг связаны лёгкой невесомой нерастяжимой нитью. В некоторый момент времени на брусок массой m2 начинает действовать сила F = 10 Н, в результате чего бруски начинают поступательное движение. Найти ускорение системы брусков. Поверхность и бруски считать гладкими.
Решение
1. После того как на второй брусок начинает действовать сила F, система начинает двигаться поступательно, поэтому оба тела можно принять за материальные точки.
 Рис. 2. Иллюстрация к примеру 1
Рис. 2. Иллюстрация к примеру 1
2. В качестве тела отсчёта выберем неподвижную плоскость, по которой движутся бруски. Пусть ось ОХ направлена в сторону движения брусков: так как сила F направлена вправо, система будет двигаться в направлении данной силы (рис. 2). Ось OY направлена перпендикулярно оси ОХ.
Изобразим силы, действующие на бруски. Силы упругости, возникающие в нити, изображать не обязательно, так как в данном случае мы не будем применять второй закон Ньютона к нити, связывающей тела.
3. Поскольку нить нерастяжима, то ускорение связанных тел будет одинаково. Запишем второй закон Ньютона в векторной форме для первого и для второго бруска:
;
.
4. Запишем второй закон Ньютона для каждого из тел в проекциях на координатные оси:
;
;
;
;
5. Как мы уже знаем, при движении связанных невесомой нитью тел силы натяжения нити Т1 и Т2, приложенные к телам, равны по модулю:
.
6. Обратим внимание, что для решения поставленной задачи достаточно решить систему из уравнений на ось OX.
Решаем полученную систему относительно неизвестного ускорения методом сложения:
Тогда
.
Ответ: .
Пример 2
Через неподвижный невесомый блок перекинута лёгкая нерастяжимая нить. К концам нити прикрепляют грузы массами m1 = 5 кг и m2 = 10 кг, затем их одновременно отпускают. Найти ускорение системы грузов.
Решение
 Рис. 3. Иллюстрация к примеру 2
Рис. 3. Иллюстрация к примеру 2
1. После того как грузы отпускают, они начинают двигаться поступательно, поэтому оба тела можно принять за материальные точки.
2. В качестве тела отсчёта выберем неподвижную плоскость, к которой прикреплён блок. Пусть ось ОY направлена в сторону движения брусков: так как брусок массой m2 тяжелее, система будет двигаться в направлении силы (рис. 3).
Ось OХ направлена перпендикулярно оси ОY.
3. Поскольку нить нерастяжима, то ускорение связанных тел будет одинаково. Запишем второй закон Ньютона в векторной форме для первого и для второго тела:
;
.
4. Запишем второй закон Ньютона для каждого из тел в проекциях на координатные оси. Учтём, что в выбранной системе отсчёта проекции ускорения и сил на ось абсцисс равны нулю, поэтому проекции на данную ось можно не рассматривать.
Так как первое тело движется вверх, проекция ускорения данного тела на ось ординат будет отрицательна.
;
.
5. Как мы уже знаем, при движении тел, связанных невесомой нитью, силы натяжения нити Т1 и Т2, приложенные к телам, равны по модулю:
.
6. Решаем полученную систему относительно неизвестного ускорения методом сложения:
Тогда
.
Ответ: .
Пример 3
К одному концу нерастяжимой верёвки массой 0,5 кг привязывают груз массой 2 кг. Верёвку вместе с грузом поднимают вертикально вверх, прикладывая силу, равную 50 Н. Найти ускорение системы, а также модули сил упругости, действующие на противоположные концы верёвки.
Решение
1. Верёвка по условию задачи нерастяжима, примем, что груз и верёвка движутся поступательно, поэтому оба тела можно принять за материальные точки.
 Рис. 4. Иллюстрация к примеру 3: силы, действующие на бруски
Рис. 4. Иллюстрация к примеру 3: силы, действующие на бруски
2. В качестве тела отсчёта выберем поверхность Земли. Ось ОY направим в сторону движения
системы — в направлении действия силы (рис. 4). Обозначим массу груза m2, массу верёвки m1.
К верхнему концу верёвки, к точке А, по условию приложена сила , в этой точке возникает сила упругости , действующая на источник силы (например, на руку человека, который тянет верёвку).
В месте крепления груза, в точке В, на верёвку действует вес груза , в результате в этой точке возникает сила упругости , действующая на груз.
3. Запишем второй закон Ньютона в векторной форме для верёвки и для груза:
;
.
4. Запишем второй закон Ньютона для каждого из тел в проекциях на ось ординат:
;
.
5. По третьему закону Ньютона силы и равны по модулю и противоположны по направлению:
.
6. Решаем полученную систему с учётом соотношения:
Тогда
.
Найдём Т2:
.
Наконец, найдём значение силы Т1: согласно третьему закону Ньютона, данная сила будет равна по модулю и противоположна по направлению силе, с которой верёвку тянут вверх:
.
Ответ: ; ; .
Упражнение 1
1. Два бруска массами m1 = 1 кг и m2 = 3 кг связаны лёгкой невесомой нерастяжимой нитью. В некоторый момент времени на брусок массой m2 начинает действовать сила F = 20 Н, в результате чего бруски начинают поступательное движение. Найти ускорение системы брусков, если коэффициент трения между поверхностью и брусками равен 0,4.
2. На нерастяжимой невесомой нити, перекинутой через неподвижный блок, подвешены грузы массами 300 и 500 г. Какова сила натяжения нити во время движения?
3. Тепловоз массой 80 т тянет два вагона массой по 20 т каждый с ускорением 0,2 м/с2. Найти силу тяги тепловоза, если коэффициент трения равен 0,005.
Упражнение 1
1. а = 1 м/с2
2. T = 3,75 Н
3. F = 30 кН



