- Преобразования энергии при механических колебаниях
- Период колебаний пружинного и математического маятников
- знать формулы для расчёта механической энергии пружинного маятника; формулы периода пружинного и математического маятников
- уметь объяснять, какие превращения энергии происходят в процессе механических колебаний
- В какой момент времени скорость груза пружинного маятника максимальна?
- Чему равна потенциальная энергия пружины, когда груз находится в положении равновесия?
- Как вычисляется механическая энергия пружинного маятника?
Преобразования энергии при механических колебаниях
Рассмотрим превращения энергии, происходящие в процессе движения пружинного маятника (рис. 1).
Нам уже известно, что механическая энергия системы Eмех изменится только при совершении работы внутренними силами трения или в случае совершения работы над телами системы внешними силами.
Пусть в колебательной системе сумма работ сил трения и внешних сил равна нулю: Aтр + Aex = 0. Тогда, согласно закону сохранения механической энергии, механическая энергия системы остаётся неизменной с течением времени:
или .
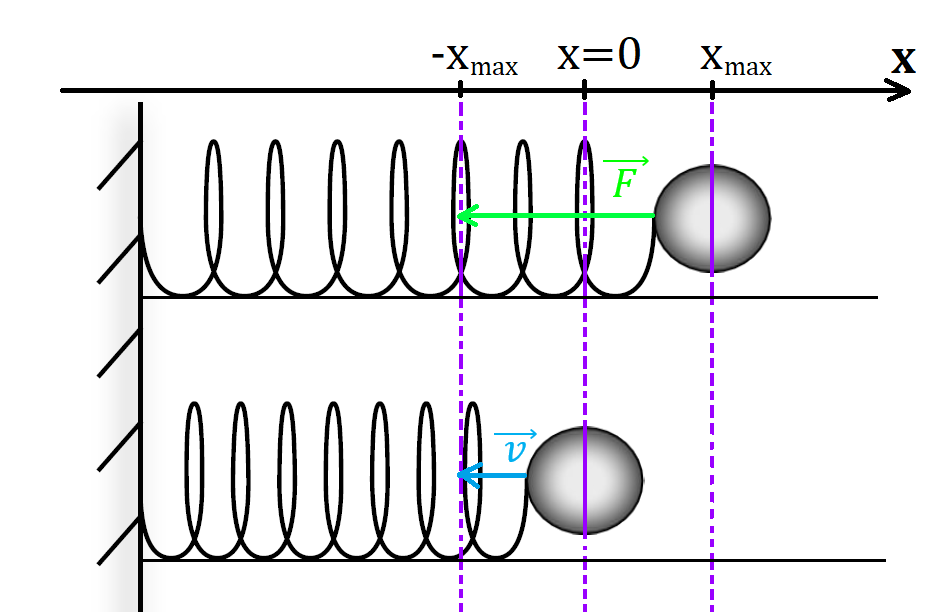 Рис. 1. Превращения энергии в пружинном маятнике
Рис. 1. Превращения энергии в пружинном маятнике
Пусть маятник начинает движение из крайнего правого положения, соответствующего координате х = хmax.
В данной точке пружина максимально растянута, потенциальная энергия пружины равна:
.
Скорость тела в данной точке равна нулю, а значит и кинетическая энергия тоже равна нулю:
.
Тогда механическая энергия системы равна:
.
Двигаясь к положению равновесия, смещение тела уменьшается, а скорость растёт. В некоторый момент времени, когда маятник находится между точками с координатами х = хmax и х = 0, координата тела равна х, а скорость — .
Тогда потенциальная энергия маятника в данный момент времени равна
.
Кинетическая энергия в рассматриваемый момент времени равна
.
Механическая энергия равна сумме кинетической и потенциальной энергии системы:
.
Оказавшись в точке с координатой х = 0, система пришла в положение равновесия. Пружина находится в недеформированном состоянии, смещение тела равно нулю, следовательно, потенциальная энергия пружины также равна нулю:
.
С другой стороны, в данной точке шарик достиг максимального значения своей скорости , тогда кинетическая энергия тела в данной точке равна:
.
Тогда механическая энергия системы равна:
.
Учтём, что по закону сохранения энергии механическая энергия во всех рассмотренных моментах времени одинакова:
.
В соответствии с уравнениями выше получаем:
.
Проанализируем полученное выражение.
Во-первых, отметим, что в процессе колебательного движения сумма кинетической и потенциальной энергий остаётся постоянной. Если пружина растягивается, то есть увеличивается первое слагаемое, то скорость тела уменьшается — уменьшается второе слагаемое. Если увеличивается потенциальная энергия колебательной системы, одновременно уменьшается кинетическая энергия.
Во-вторых, из равенства выше следует, что максимальная потенциальная энергия колебательной системы равна максимальной кинетической энергии.
Наконец, используем это соотношение, чтобы вывести формулы максимальной скорости и максимального смещения маятника:
;
.
Таким образом, чем больше амплитуда колебаний пружинного маятника, тем большую скорость он разовьёт при прохождении положения равновесия. Чем больше скорость маятника, тем больше величина его смещения относительно положения равновесия.
Соотношение выше также позволяет найти скорость маятника, если известна амплитуда колебаний и текущее положение:
,
а также найти координату маятника в любой момент времени, если известна максимальная скорость в положении равновесия и скорость в рассматриваемый момент времени:
.
Полученные закономерности справедливы и для математического маятника: если механическая энергия в процессе колебательного движения остаётся неизменной, то при прохождении положения равновесия маятник имеет максимальную скорость и максимальную кинетическую энергию, при удалении от положения равновесия кинетическая энергия маятника уменьшается, а потенциальная энергия увеличивается до некоторого максимального значения. При движении к положению устойчивого равновесия, напротив, кинетическая энергия маятника увеличивается, а потенциальная уменьшается.
Период колебаний пружинного и математического маятников
Выражение показывает, что модуль максимальной скорости грузика увеличится при увеличении жёсткости пружины и уменьшении массы груза. Чем быстрее движется маятник, тем меньше период его колебаний.
Понятно, что возвращающая сила упругости в колебательной системе будет тем больше, чем больше коэффициент жёсткости пружины k. С другой стороны, чем легче грузик, тем он менее инертен, тем больше будет его скорость. С точки зрения динамики также получается, что скорость маятника будет тем больше, чем больше коэффициент жёсткости и чем меньше масса груза.
Зависимость между периодом колебаний пружинного маятника, жёсткостью пружины и массой груза установлена экспериментально:
,
где T [с] — период колебаний пружинного маятника;
m [кг] — масса колеблющегося груза;
k [Н/м] — коэффициент жёсткости.
Период свободных гармонических колебаний пружинного маятника, состоящего из груза массой m и лёгкой пружины жёсткостью k, равен
.
Формула выше показывает, что при увеличении массы груза в 9 раз период колебаний маятника увеличится в 3 раза; при увеличении жёсткости пружины в 16 раз период колебаний уменьшится в 4 раза.
Период колебаний математического маятника не зависит от массы колеблющегося груза. Это связано с тем, что и кинетическая энергия груза, и его потенциальная энергия прямо пропорциональны массе груза. Период колебаний математического маятника зависит только от длины нити:
,
где T [с] — период колебаний математического маятника;
[м] — длина нити;
g = 10 м/с2 — модуль ускорения свободного падения.
Период свободных гармонических колебаний математического маятника, длина нити которого равна , рассчитывается по следующей формуле:
.
Таким образом, при уменьшении длины нити маятника в 4 раза период колебаний математического маятника уменьшится в 2 раза.
Эту формулу можно объяснить с точки зрения динамики движения груза: чем больше ускорение свободного падения, тем больше возвращающая сила тяжести, действующая на груз, тем больше его скорость и тем меньше период колебаний маятника.
Пример 1
Шарик массой 80 г, прикреплённый к одному из концов лёгкой пружины жёсткостью 250 Н/м, совершает свободные гармонические колебания в горизонтальном направлении. Определите максимальное отклонение шарика от положения равновесия, если в некоторый момент времени его скорость равна 3 м/с, а отклонение от положения равновесия в этот же момент было 4 см. Трением пренебречь.
Решение
1. Перечислим исходные данные:
2. В крайних точках от положения равновесия тело обладает максимальной потенциальной энергией, а кинетическая энергия равна нулю, тогда механическая энергию будет
.
3. Запишем, чему равна механическая энергия в некоторый момент времени, когда шарик двигался со скоростью 3 м/с и отклонялся на 4 см:
.
С другой стороны, в отсутствие трения механическая энергия сохраняется, а значит
.
4. Из последнего равенства выразим ∆xmax:
м.
Ответ: м.
Итоги
- Механическая энергия пружинного маятника при отсутствии потерь энергии в системе в любой момент времени постоянна и равна: .
- Период свободных гармонических колебаний пружинного маятника, состоящего из груза массой m и лёгкой пружины жёсткостью k, равен .
- Период свободных гармонических колебаний математического маятника, длина нити которого равна l, рассчитывается по следующей формуле: .
Упражнение 1
1. Ученик проводил эксперименты с пружинным маятником. Сначала он определил, что амплитуда колебаний шарика массой 0,01 кг, прикреплённого к пружине, равна см. Далее ученик хотел узнать значение скорости в момент времени, когда отклонение шарика от положения равновесия составляло см. Какое значение скорости было получено? Жёсткость пружины 300 Н/м.
2. Определите период колебаний пружинного маятника, состоящего из груза массой 0,3 кг и пружины жёсткостью 400 Н/м.
3. Чему равен период колебаний математического маятника, если груз подвешен на нити длинной 1,5 м?
Контрольные вопросы
1. Как рассчитать механическую энергию пружинного маятника?
2. От чего зависит период колебаний пружинного маятника?
3. Как рассчитывается период колебаний математического маятника?
Упражнение 1
1. м/с
2. с
3. с
- Преобразования энергии при механических колебаниях
- Период колебаний пружинного и математического маятников
- знать формулы для расчёта механической энергии пружинного маятника; формулы периода пружинного и математического маятников
- уметь объяснять, какие превращения энергии происходят в процессе механических колебаний
- В какой момент времени скорость груза пружинного маятника максимальна?
- Чему равна потенциальная энергия пружины, когда груз находится в положении равновесия?
- Как вычисляется механическая энергия пружинного маятника?
Преобразования энергии при механических колебаниях
Рассмотрим превращения энергии, происходящие в процессе движения пружинного маятника (рис. 1).
Нам уже известно, что механическая энергия системы Eмех изменится только при совершении работы внутренними силами трения или в случае совершения работы над телами системы внешними силами.
Пусть в колебательной системе сумма работ сил трения и внешних сил равна нулю: Aтр + Aex = 0. Тогда, согласно закону сохранения механической энергии, механическая энергия системы остаётся неизменной с течением времени:
или .
 Рис. 1. Превращения энергии в пружинном маятнике
Рис. 1. Превращения энергии в пружинном маятнике
Пусть маятник начинает движение из крайнего правого положения, соответствующего координате х = хmax.
В данной точке пружина максимально растянута, потенциальная энергия пружины равна:
.
Скорость тела в данной точке равна нулю, а значит и кинетическая энергия тоже равна нулю:
.
Тогда механическая энергия системы равна:
.
Двигаясь к положению равновесия, смещение тела уменьшается, а скорость растёт. В некоторый момент времени, когда маятник находится между точками с координатами х = хmax и х = 0, координата тела равна х, а скорость — .
Тогда потенциальная энергия маятника в данный момент времени равна
.
Кинетическая энергия в рассматриваемый момент времени равна
.
Механическая энергия равна сумме кинетической и потенциальной энергии системы:
.
Оказавшись в точке с координатой х = 0, система пришла в положение равновесия. Пружина находится в недеформированном состоянии, смещение тела равно нулю, следовательно, потенциальная энергия пружины также равна нулю:
.
С другой стороны, в данной точке шарик достиг максимального значения своей скорости , тогда кинетическая энергия тела в данной точке равна:
.
Тогда механическая энергия системы равна:
.
Учтём, что по закону сохранения энергии механическая энергия во всех рассмотренных моментах времени одинакова:
.
В соответствии с уравнениями выше получаем:
.
Проанализируем полученное выражение.
Во-первых, отметим, что в процессе колебательного движения сумма кинетической и потенциальной энергий остаётся постоянной. Если пружина растягивается, то есть увеличивается первое слагаемое, то скорость тела уменьшается — уменьшается второе слагаемое. Если увеличивается потенциальная энергия колебательной системы, одновременно уменьшается кинетическая энергия.
Во-вторых, из равенства выше следует, что максимальная потенциальная энергия колебательной системы равна максимальной кинетической энергии.
Наконец, используем это соотношение, чтобы вывести формулы максимальной скорости и максимального смещения маятника:
;
.
Таким образом, чем больше амплитуда колебаний пружинного маятника, тем большую скорость он разовьёт при прохождении положения равновесия. Чем больше скорость маятника, тем больше величина его смещения относительно положения равновесия.
Соотношение выше также позволяет найти скорость маятника, если известна амплитуда колебаний и текущее положение:
,
а также найти координату маятника в любой момент времени, если известна максимальная скорость в положении равновесия и скорость в рассматриваемый момент времени:
.
Полученные закономерности справедливы и для математического маятника: если механическая энергия в процессе колебательного движения остаётся неизменной, то при прохождении положения равновесия маятник имеет максимальную скорость и максимальную кинетическую энергию, при удалении от положения равновесия кинетическая энергия маятника уменьшается, а потенциальная энергия увеличивается до некоторого максимального значения. При движении к положению устойчивого равновесия, напротив, кинетическая энергия маятника увеличивается, а потенциальная уменьшается.
Период колебаний пружинного и математического маятников
Выражение показывает, что модуль максимальной скорости грузика увеличится при увеличении жёсткости пружины и уменьшении массы груза. Чем быстрее движется маятник, тем меньше период его колебаний.
Понятно, что возвращающая сила упругости в колебательной системе будет тем больше, чем больше коэффициент жёсткости пружины k. С другой стороны, чем легче грузик, тем он менее инертен, тем больше будет его скорость. С точки зрения динамики также получается, что скорость маятника будет тем больше, чем больше коэффициент жёсткости и чем меньше масса груза.
Зависимость между периодом колебаний пружинного маятника, жёсткостью пружины и массой груза установлена экспериментально:
,
где T [с] — период колебаний пружинного маятника;
m [кг] — масса колеблющегося груза;
k [Н/м] — коэффициент жёсткости.
Период свободных гармонических колебаний пружинного маятника, состоящего из груза массой m и лёгкой пружины жёсткостью k, равен
.
Формула выше показывает, что при увеличении массы груза в 9 раз период колебаний маятника увеличится в 3 раза; при увеличении жёсткости пружины в 16 раз период колебаний уменьшится в 4 раза.
Период колебаний математического маятника не зависит от массы колеблющегося груза. Это связано с тем, что и кинетическая энергия груза, и его потенциальная энергия прямо пропорциональны массе груза. Период колебаний математического маятника зависит только от длины нити:
,
где T [с] — период колебаний математического маятника;
[м] — длина нити;
g = 10 м/с2 — модуль ускорения свободного падения.
Период свободных гармонических колебаний математического маятника, длина нити которого равна , рассчитывается по следующей формуле:
.
Таким образом, при уменьшении длины нити маятника в 4 раза период колебаний математического маятника уменьшится в 2 раза.
Эту формулу можно объяснить с точки зрения динамики движения груза: чем больше ускорение свободного падения, тем больше возвращающая сила тяжести, действующая на груз, тем больше его скорость и тем меньше период колебаний маятника.
Пример 1
Шарик массой 80 г, прикреплённый к одному из концов лёгкой пружины жёсткостью 250 Н/м, совершает свободные гармонические колебания в горизонтальном направлении. Определите максимальное отклонение шарика от положения равновесия, если в некоторый момент времени его скорость равна 3 м/с, а отклонение от положения равновесия в этот же момент было 4 см. Трением пренебречь.
Решение
1. Перечислим исходные данные:
2. В крайних точках от положения равновесия тело обладает максимальной потенциальной энергией, а кинетическая энергия равна нулю, тогда механическая энергию будет
.
3. Запишем, чему равна механическая энергия в некоторый момент времени, когда шарик двигался со скоростью 3 м/с и отклонялся на 4 см:
.
С другой стороны, в отсутствие трения механическая энергия сохраняется, а значит
.
4. Из последнего равенства выразим ∆xmax:
м.
Ответ: м.
Итоги
- Механическая энергия пружинного маятника при отсутствии потерь энергии в системе в любой момент времени постоянна и равна: .
- Период свободных гармонических колебаний пружинного маятника, состоящего из груза массой m и лёгкой пружины жёсткостью k, равен .
- Период свободных гармонических колебаний математического маятника, длина нити которого равна l, рассчитывается по следующей формуле: .
Упражнение 1
1. Ученик проводил эксперименты с пружинным маятником. Сначала он определил, что амплитуда колебаний шарика массой 0,01 кг, прикреплённого к пружине, равна см. Далее ученик хотел узнать значение скорости в момент времени, когда отклонение шарика от положения равновесия составляло см. Какое значение скорости было получено? Жёсткость пружины 300 Н/м.
2. Определите период колебаний пружинного маятника, состоящего из груза массой 0,3 кг и пружины жёсткостью 400 Н/м.
3. Чему равен период колебаний математического маятника, если груз подвешен на нити длинной 1,5 м?
Контрольные вопросы
1. Как рассчитать механическую энергию пружинного маятника?
2. От чего зависит период колебаний пружинного маятника?
3. Как рассчитывается период колебаний математического маятника?
Упражнение 1
1. м/с
2. с
3. с



