Все уроки по всем предметам школьной программы ФГОС

Перпендикуляр и наклонные

План урока

Расстояние от точки до плоскости;
Теорема о трех перпендикулярах.

Цели урока

Знать, что такое перпендикуляр к плоскости, наклонная и проекция наклонной на плоскость;
Знать, как измеряется расстояние от точки до плоскости, между параллельными плоскостями, между прямой и параллельной ей плоскостью;
Знать и уметь применять теорему о трёх перпендикулярах.

Разминка

При каком условии прямая называется перпендикулярной к плоскости?
Что называют расстоянием от точки до прямой?
Как определяется угол между прямыми в пространстве?

Расстояние от точки до плоскости

Определение 1

Перпендикуляром, проведенным из данной точки на данную плоскость, называется отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, перпендикулярной к плоскости.

Рис. 1.

На рисунке 1 показана прямая n, проведённая через точку $A$ , перпендикулярно к плоскости $α$ . Прямая n и плоскость $α$ пересекаются в точке $H$ . Отрезок $A H$ в данном случае и является перпендикуляром, проведённым из точки $A$ к плоскости $α$ .

Определение 2

Наклонной, проведённой из данной точки к данной плоскости, называется любой отрезок, соединяющий данную точку с точкой плоскости, не являющийся перпендикуляром к плоскости.

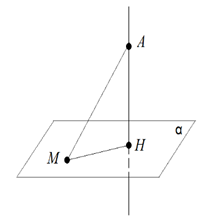Рис. 2.

На рисунке 2 показаны перпендикуляр $A H$ и наклонная $A M$ проведённые из одной и той же точки $A$ . Точку $H$ , при этом, называют основанием перпендикуляра, а точку $M$ – основанием наклонной.

Отрезок $M H$ называют проекцией наклонной $A M$ на плоскость $α$ .

Определение 3

Отрезок, соединяющий основания перпендикуляра и наклонной, проведённых из одной и той же точки, называется проекцией наклонной.

Сравним перпендикуляр $A H$ и наклонную AM (рис. 2).

Рассмотрим треугольник $A H M$ . $∠ A H M = 90 °$ , так как $A H$ – перпендикуляр к плоскости. Значит, $Δ A H M$ – прямоугольный. При этом $A M$ – гипотенуза, а $A H$ – катет прямоугольного треугольника $A H M$ . Следовательно, $A H < A M$ .

Таким образом, перпендикуляр, проведённый из данной точки к плоскости, меньше любой наклонной, проведённой из той же точки к этой плоскости. Это означает, что из всех расстояний от точки $A$ до различных точек плоскости $α$ наименьшим является расстояние до точки $H$ . За расстояние от точки $A$ до плоскости $α$ принимают длину именно этого отрезка $A H$ .

Определение 4

Расстоянием от точки до плоскости называют длину перпендикуляра, проведённого из данной точки к данной плоскости.

С расстоянием от точки до плоскости связаны следующие понятия:

расстояние между параллельными плоскостями,
расстояние между прямой и параллельной ей плоскостью,
расстояние между скрещивающимися прямыми.

Сформулируем определения этих понятий.

Определение 5

Расстоянием между параллельными плоскостями называют расстояние от произвольной точки одной из параллельных плоскостей до другой плоскости.

Определение 6

Расстоянием между прямой и параллельной ей плоскостью называют расстояние от любой точки данной прямой до данной плоскости.

Определение 7

Расстоянием между скрещивающимися прямыми называют расстояние от произвольной точки одной из скрещивающихся прямых до плоскости, проходящей через другую прямую параллельно первой прямой.

Пример 1

Докажите, что если прямая параллельна плоскости, то все её точки находятся на одинаковом расстоянии от плоскости.

Доказательство

Рис. 3. К примеру 1

Пусть $a$ – данная прямая и $α$ – данная плоскость (рис. 3). Возьмём на прямой $a$ две произвольные точки $X$ и $Y$ . Их расстояния до плоскости $α$ – это длины перпендикуляров $X X_{1}$ и $Y Y_{1}$ , опущенных на эту плоскость. Так как $X X_{1} ⊥ α$ и $Y Y_{1} ⊥ α$ , то $X X_{1} ∥ Y Y_{1}$ , значит, лежат в одной плоскости. Эта плоскость пересекает плоскость $α$ по прямой $X_{1} Y_{1}$ . Прямая a параллельна прямой $X_{1} Y_{1}$ , так как не пересекает содержащую её плоскость $α$ . Таким образом, у четырёхугольника $X X_{1} Y_{1} Y$ противолежащие стороны параллельны. Значит, он параллелограмм, следовательно, $X X_{1} = Y Y_{1}$ . Точки $X$ и $Y$ были выбраны произвольно на прямой $a$ , а значит все точки прямой $a$ находятся на одинаковом расстоянии от плоскости $α$ . Что и требовалось доказать.

Упражнение 1

1. Из некоторой точки проведены к данной плоскости перпендикуляр и наклонная, угол между которыми равен $30 °$ . Найдите наклонную и её проекцию на данную плоскость, если перпендикуляр равен 6 см.

2. Расстояние от точки $A$ до каждой из вершин правильного треугольника $M N K$ равно 8 см. Найдите расстояние от точки $A$ до плоскости $M N K$ , если $M N = 12 с м$ .

3. Через вершину прямого угла $C$ прямоугольного треугольника $A B C$ проведена плоскость параллельная гипотенузе, на расстоянии 1 м от неё. Проекции катетов на эту плоскость равны 3 м и 5 м. Найдите гипотенузу.

4. Через одну сторону ромба проведена плоскость на расстоянии 4 м от противолежащей стороны. Проекции диагоналей на эту плоскость равны 8 м и 2 м. Найдите проекции сторон.

Теорема о трёх перпендикулярах

Теорема 1

Прямая, проведённая в плоскости через основание наклонной перпендикулярно к её проекции на эту плоскость, перпендикулярна и к самой наклонной.

Доказательство

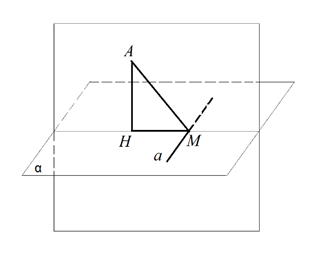Рис. 4. К доказательству теоремы 1

На рисунке 4 отрезок $A H$ – перпендикуляр к плоскости $α$ , $A M$ – наклонная, $a$ – прямая, проведённая в плоскости $α$ через точку $M$ перпендикулярно к проекции $H M$ наклонной. Докажем, что прямая a перпендикулярна наклонной $A M$ .

$a ⊥ H M$ по условию и $a ⊥ A H$ , так как $A H ⊥ α$ .

Следовательно, прямая $a$ перпендикулярна к плоскости треугольника $A M H$ , так как она перпендикулярна к двум пересекающимся прямым $A H$ и $H M$ , лежащим в этой плоскости. Значит, прямая a перпендикулярна к любой прямой, лежащей в плоскости $A M H$ . Поэтому, $a ⊥ A M$ .

Теорема доказана.

Справедливо также и обратное утверждение: прямая, проведённая в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна и к её проекции.

Пример 2

Через центр вписанной в треугольник окружности проведена прямая, перпендикулярная плоскости треугольника. Докажите, что каждая точка этой прямой равноудалена от сторон треугольника.

Решение

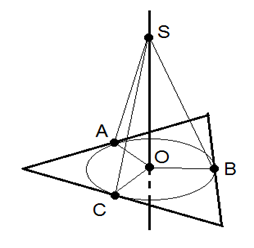Рис. 5. К примеру 2

Пусть $A, B, C$ – точка касания сторон треугольника с окружностью, то есть стороны треугольника являются касательными к окружности, $O$ – центр окружности и $S$ – точка на перпендикуляре (рис. 5). Так как радиус $O A$ перпендикулярен стороне треугольника, то по теореме о трёх перпендикулярах отрезок $S A$ есть перпендикуляр к этой стороне, а его длина – расстояние от точки $S$ до стороны треугольника.

По теореме Пифагора $S A = \sqrt{A O^{2} + O S^{2}} = \sqrt{r^{2} + O S^{2}}$ , где $r$ – радиус вписанной окружности. Аналогично находим $S B = \sqrt{r^{2} + O S^{2}}$ , $S C = \sqrt{r^{2} + O S^{2}}$ , т.е. все расстояния от точки $S$ до сторон треугольника равны.

Упражнение 2

1. К плоскости треугольника из центра вписанной в него окружности радиуса $0, 7 м$ восстановлен перпендикуляр длиной $2, 4 м$ . Найдите расстояние от конца этого перпендикуляра до сторон треугольника.

2. Расстояние от данной точки до плоскости треугольника равно $1, 1 м$ , а до каждой из его сторон – $6, 1 м$ . Найдите расстояние от основания этого перпендикуляра до сторон треугольника.

3. Из вершины равностороннего треугольника $A B C$ восстановлен перпендикуляр $A D$ к плоскости треугольника. Найдите расстояние от точки $D$ до стороны $B C$ , если $A D = 13 с м, B C = 6 с м$ .

4. Расстояния от точки $A$ до всех сторон квадрата равны $a$ . Найдите расстояние от точки $A$ до плоскости квадрата, если диагональ квадрата равна $d$ .

Контрольные вопросы

Что такое перпендикуляр и наклонная к плоскости?
Что называют проекцией наклонной на плоскость?
Что принимают за расстояние от точки до плоскости?
Сформулируйте теорему о трёх перпендикулярах.

Ответы

Упражнение 1

Наклонная равна $4 \sqrt{3}$ см; проекция равна $2 \sqrt{3}$ см.
4 см.
6 м.
5 м и 3 м.

Упражнение 2

2,5 м.
6 м.
14 см.
$\sqrt{a^{2} - \frac{d^{2}}{8}}$

Конспект урока: Расстояние от точки до плоскости. Теорема о трёх перпендикулярах

Взаимное расположение прямых и плоскостей в пространстве

Расстояние от точки до плоскости

Теорема о трёх перпендикулярах