- Угол между прямой и плоскостью
- Знать, что называется углом между прямой и плоскостью
- Уметь находить угол между прямой и плоскостью
- Что называют перпендикуляром к плоскости?
- Что называют наклонной к плоскости и её проекцией на плоскость?
- Как определяется угол между прямыми в пространстве?
Угол между прямой и плоскостью
Введём понятие проекции произвольной фигуры на плоскость, но перед этим дадим определение проекции точки на плоскость.
Проекцией точки на плоскость называется основание перпендикуляра, проведённого из этой точки к плоскости, если точка не лежит в плоскости, и сама точка, если она лежит в плоскости.
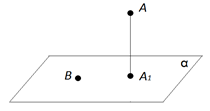 Рис. 1.
Рис. 1.
На рисунке 1 точка – проекция точки на плоскость , а точка , которая лежит в плоскости – проекция самой точки на эту плоскость.
Пусть в пространстве дана некоторая фигура . Если простроить проекции всех точек фигуры на плоскость , то фигура , состоящая из этих проекций, называется проекцией фигуры на плоскость .
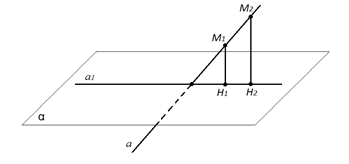 Рис. 2.
Рис. 2.
Чтобы построить проекцию прямой на плоскость , не перпендикулярную к этой прямой, надо взять две произвольные точки и лежащие на прямой и найти их проекции и на плоскость . Тогда проекцией прямой a на плоскость является прямая проходящая через точки и (рис. 2). Проекцией отрезка MN на плоскость, не перпендикулярную к нему, является отрезок, концы которого – проекции точек M и N на эту плоскость.
Дадим теперь определение угла между прямой и плоскостью.
Углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, называется угол между прямой и её проекцией на плоскость.
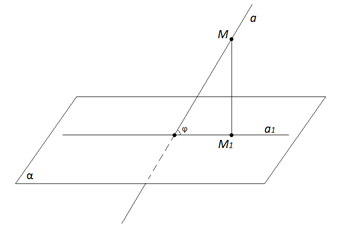 Рис. 3.
Рис. 3.
На рисунке 3 показана прямая , пересекающая плоскость и проекция этой прямой на данную плоскость. Угол между прямой и проекцией есть угол между прямой и плоскостью .
В случае, если прямая перпендикулярна к плоскости, то её проекцией на эту плоскость будет точка пересечения этой прямой с плоскостью. В этом случае угол между прямой и плоскостью считается прямым и равен .
Пример 1
Точка A отстоит от плоскости на расстоянии 8 см. Найдите длину наклонной, проведённой из этой точки под углом к плоскости, равным .
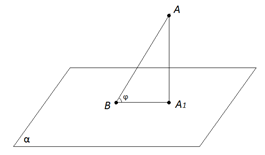 Рис. 4.
Рис. 4.
Решение
Опустим перпендикуляр на плоскость (рис. 4). В таком случае - наклонная к плоскости, - её проекция на плоскость, а - угол между прямой и плоскостью Получили треугольник с прямым углом при вершине , где острый угол этого треугольника, противолежащий катету , равен . Следовательно, .
Ответ: 16 см.
Пример 2
Отрезок длиной 10 м пересекает плоскость, концы его находятся на расстояниях 2 м и 3 м от плоскости. Найдите угол между данным отрезком и плоскостью.
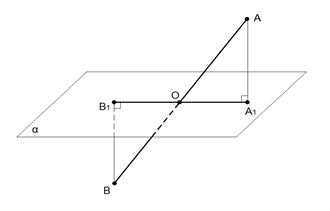 Рис. 5.
Рис. 5.
Решение
Обозначим концы данного отрезка буквами и , плоскость – буквой , точку пересечения отрезка с плоскостью буквой , а проекции точек и на плоскость буквами соответственно и (рис. 5).
Углом между отрезком и плоскостью является угол .
По условию задачи , расстояния от точек и до плоскости равны соответственно 2 м и 3 м. Значит , .
Треугольники и подобны, так как (прямые) и (вертикальные).
Из подобия треугольников следует .
Обозначим . Тогда .
Получим уравнение
,
,
,
,
,
.
Получили .
Таким образом, .
Ответ: .
Пример 3
Через катет равнобедренного прямоугольного треугольника проведена плоскость под углом ко второму катету. Найдите угол между гипотенузой и плоскостью.
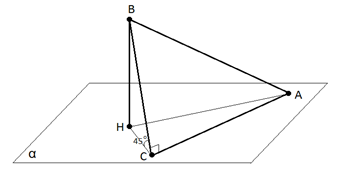 Рис. 6.
Рис. 6.
Решение
Пусть катет прямоугольного треугольника с прямым углом лежит в плоскости (рис. 6). По условию задачи катеты и равны. Катет наклонён к плоскости под углом в . Проведём перпендикуляр к плоскости. Получим еще один прямоугольный треугольник с прямым углом при вершине . Так как , то и . Следовательно, треугольник равнобедренный. Обозначим .
Тогда .
Углом между гипотенузой и плоскостью является угол .
.
Ответ: .
Упражнение 1
1. Из точки, отстоящей от плоскости на расстоянии 5 см, проведены две наклонные под углом 30o к плоскости, причём их проекции образуют угол 120o. Найдите расстояние между концами наклонных.
2. Из точки к плоскости проведены две наклонные. Одна из наклонных равна 10 см и имеет проекцию длиной 8 см. Найдите длину второй наклонной, если она образует с данной плоскостью угол 30o.
Контрольные вопросы
- Что называют проекцией точки на плоскость?
- Что называют проекцией фигуры на плоскость?
- Как построить проекцию прямой на плоскость?
- Какой угол принимают за угол между прямой и плоскостью?
Упражнение 1
- 15 см.
- 12 см.
- Угол между прямой и плоскостью
- Знать, что называется углом между прямой и плоскостью
- Уметь находить угол между прямой и плоскостью
- Что называют перпендикуляром к плоскости?
- Что называют наклонной к плоскости и её проекцией на плоскость?
- Как определяется угол между прямыми в пространстве?
Угол между прямой и плоскостью
Введём понятие проекции произвольной фигуры на плоскость, но перед этим дадим определение проекции точки на плоскость.
Проекцией точки на плоскость называется основание перпендикуляра, проведённого из этой точки к плоскости, если точка не лежит в плоскости, и сама точка, если она лежит в плоскости.
 Рис. 1.
Рис. 1.
На рисунке 1 точка – проекция точки на плоскость , а точка , которая лежит в плоскости – проекция самой точки на эту плоскость.
Пусть в пространстве дана некоторая фигура . Если простроить проекции всех точек фигуры на плоскость , то фигура , состоящая из этих проекций, называется проекцией фигуры на плоскость .
 Рис. 2.
Рис. 2.
Чтобы построить проекцию прямой на плоскость , не перпендикулярную к этой прямой, надо взять две произвольные точки и лежащие на прямой и найти их проекции и на плоскость . Тогда проекцией прямой a на плоскость является прямая проходящая через точки и (рис. 2). Проекцией отрезка MN на плоскость, не перпендикулярную к нему, является отрезок, концы которого – проекции точек M и N на эту плоскость.
Дадим теперь определение угла между прямой и плоскостью.
Углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, называется угол между прямой и её проекцией на плоскость.
 Рис. 3.
Рис. 3.
На рисунке 3 показана прямая , пересекающая плоскость и проекция этой прямой на данную плоскость. Угол между прямой и проекцией есть угол между прямой и плоскостью .
В случае, если прямая перпендикулярна к плоскости, то её проекцией на эту плоскость будет точка пересечения этой прямой с плоскостью. В этом случае угол между прямой и плоскостью считается прямым и равен .
Пример 1
Точка A отстоит от плоскости на расстоянии 8 см. Найдите длину наклонной, проведённой из этой точки под углом к плоскости, равным .
 Рис. 4.
Рис. 4.
Решение
Опустим перпендикуляр на плоскость (рис. 4). В таком случае - наклонная к плоскости, - её проекция на плоскость, а - угол между прямой и плоскостью Получили треугольник с прямым углом при вершине , где острый угол этого треугольника, противолежащий катету , равен . Следовательно, .
Ответ: 16 см.
Пример 2
Отрезок длиной 10 м пересекает плоскость, концы его находятся на расстояниях 2 м и 3 м от плоскости. Найдите угол между данным отрезком и плоскостью.
 Рис. 5.
Рис. 5.
Решение
Обозначим концы данного отрезка буквами и , плоскость – буквой , точку пересечения отрезка с плоскостью буквой , а проекции точек и на плоскость буквами соответственно и (рис. 5).
Углом между отрезком и плоскостью является угол .
По условию задачи , расстояния от точек и до плоскости равны соответственно 2 м и 3 м. Значит , .
Треугольники и подобны, так как (прямые) и (вертикальные).
Из подобия треугольников следует .
Обозначим . Тогда .
Получим уравнение
,
,
,
,
,
.
Получили .
Таким образом, .
Ответ: .
Пример 3
Через катет равнобедренного прямоугольного треугольника проведена плоскость под углом ко второму катету. Найдите угол между гипотенузой и плоскостью.
 Рис. 6.
Рис. 6.
Решение
Пусть катет прямоугольного треугольника с прямым углом лежит в плоскости (рис. 6). По условию задачи катеты и равны. Катет наклонён к плоскости под углом в . Проведём перпендикуляр к плоскости. Получим еще один прямоугольный треугольник с прямым углом при вершине . Так как , то и . Следовательно, треугольник равнобедренный. Обозначим .
Тогда .
Углом между гипотенузой и плоскостью является угол .
.
Ответ: .
Упражнение 1
1. Из точки, отстоящей от плоскости на расстоянии 5 см, проведены две наклонные под углом 30o к плоскости, причём их проекции образуют угол 120o. Найдите расстояние между концами наклонных.
2. Из точки к плоскости проведены две наклонные. Одна из наклонных равна 10 см и имеет проекцию длиной 8 см. Найдите длину второй наклонной, если она образует с данной плоскостью угол 30o.
Контрольные вопросы
- Что называют проекцией точки на плоскость?
- Что называют проекцией фигуры на плоскость?
- Как построить проекцию прямой на плоскость?
- Какой угол принимают за угол между прямой и плоскостью?
Упражнение 1
- 15 см.
- 12 см.


