Все уроки по всем предметам школьной программы ФГОС

Двугранный угол. Перпендикулярность плоскостей

План урока

Двугранный угол
Признак перпендикулярности двух плоскостей

Цели урока

Знать определение двугранного угла
Уметь определять величину двугранного угла
Знать какие плоскости называются перпендикулярными
Уметь доказывать и применять признак перпендикулярности плоскостей

Разминка

Какую фигуру на плоскости называют углом?
Какие прямые называются перпендикулярными?
Как определяется угол между прямыми на плоскости и в пространстве?

Двугранный угол

Из планиметрии мы знаем, что углом на плоскости называют фигуру, образованную двумя лучами, исходящими из одной точки. Наряду с этим в стереометрии рассматривают ещё и двугранный угол. Дадим определение этого понятия.

Двугранным углом называется фигура, образованная двумя полуплоскостями с общей ограничивающей их прямой (рис. 1). Полуплоскости называются гранями, а ограничивающая их прямая – ребром двугранного угла.

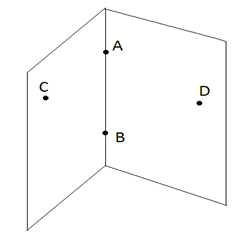Рис. 1. Двугранный угол

Если на разных гранях двугранного угла отмечены точки $C$ и $D$ , а на ребре этого угла отмечены точки $A$ и $B$ , то данный угол обозначают $C A B D$ (рис. 1).

Примерами, иллюстрирующими двугранный угол, могут быть полураскрытая книга, двускатная крыша, раскрытый ноутбук и т. д.

Углы на плоскости, как известно, можно измерить с помощью транспортира. Каким же образом можно измерить двугранные углы?

Отметим на ребре двугранного угла некоторую точку.

В каждой грани из этой точки проведём луч перпендикулярно к ребру. Величина угла, образованного этими лучами не зависит от выбора точки на ребре. Поэтому построенный таким образом угол и используют для измерения величины двугранного угла. Называют такой угол линейным углом двугранного угла.

Все линейные углы двугранного угла равны друг другу.

Градусной мерой двугранного угла называется градусная мера его линейного угла.

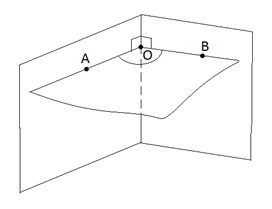Рис. 2. Линейный угол двугранного угла

На рисунке 2 из точки $O$ , лежащей на ребре двугранного ребра в каждой грани проведены перпендикуляры к этому ребру $O A$ и $O B$ . Угол $A O B$ является линейным углом двугранного угла.

Понятия прямого, острого и тупого угла распространяются и на двугранные углы.

Двугранный угол называется прямым, если он равен $90 °$ .

Двугранный угол называется острым, если он меньше $90 °$ .

Двугранный угол называется тупым, если он больше $90 °$ .

Пример 1

Из точек $A$ и $B$ , лежащих в гранях двугранного угла, опущены перпендикуляры $A A_{1}$ и $B B_{1}$ на ребро угла. Найдите длину отрезка $A B$ , если $A A_{1} = 3, B B_{1} = 4, A_{1} B_{1} = 6$ и двугранный угол равен $60 °$ .

Решение

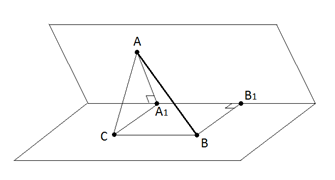Рис. 3.

Проведём прямые $A_{1} C$ параллельно $B B_{1}$ и $B C$ параллельно $A_{1} B_{1}$ (рис. 3). Четырёхугольник $A_{1} B_{1} B C$ – параллелограмм, значит, $A_{1} C = B B_{1} = 4$ . Прямая $A_{1} B_{1}$ перпендикулярна плоскости треугольника $A A_{1} C$ , так как она перпендикулярна двум прямым в этой плоскости $A A_{1}$ и $C A_{1}$ . Следовательно, параллельная ей прямая $B C$ тоже перпендикулярна этой плоскости. Значит, треугольник $A B C$ – прямоугольный с прямым углом $C$ . Из теоремы косинусов для $∆ A A_{1} C$ :

$A C = \sqrt{A A_{1}^{2} + A_{1} C^{2} - 2 \cdot A A_{1} \cdot A_{1} C \cdot \cos 60 °} =$
$= \sqrt{3^{2} + 4^{2} - 2 \cdot 3 \cdot 4 \cdot \cos 60 °} = \sqrt{13}$ .

По теореме Пифагора для треугольника $A B C$ , найдём $A B$ :

$A B = \sqrt{A C^{2} + B C^{2}} = \sqrt{13 + 6^{2}} = \sqrt{49} = 7$ .

Ответ: $7$ .

Упражнение 1

1. Двугранный угол равен $30 °$ . Точка, выбранная на одной из граней, удалена от ребра угла на 12 см. Найдите расстояние от данной точки до второй грани.

2. Равнобедренный треугольник $A B C$ и правильный треугольник $A B D$ не лежат в одной плоскости. Отрезок $B D$ является перпендикуляром к плоскости $A D C$ . Найдите двугранный угол $B A C D$ если $A B = B C = 2 \sqrt{5}$ см, $A C = 4$ см.

Признак перпендикулярности двух плоскостей

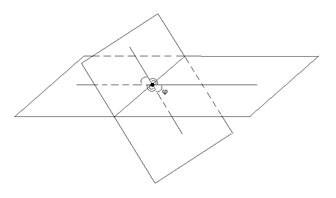Рис. 4.

При пересечении двух плоскостей образуются четыре двугранных угла с общим ребром (рис. 4).

Обозначим один из углов, а именно тот, который не превосходит $90 °$ , буквой $φ$ .

Этот угол принимают за угол между пересекающимися плоскостями.

Другие три угла равны соответственно $180 ° - φ$ , $φ$ и $180 ° - φ$ . Очевидно, что если $φ = 90 °$ , то и остальные углы равны $90 °$ .

Две пересекающиеся плоскости называются перпендикулярными, (взаимно перпендикулярными) если угол между ними равен $90 °$ .

Примером перпендикулярных плоскостей являются смежные стены комнаты, а также стена и потолок комнаты.

Сформулируем и докажем признак перпендикулярности плоскостей.

Признак перпендикулярности двух плоскостей

Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.

Доказательство

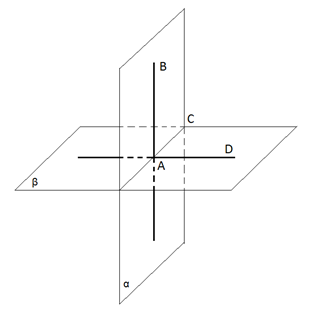Рис. 5. К доказательству теоремы 1

Пусть плоскость $α$ проходит через прямую $A B$ , перпендикулярную к плоскости $β$ и пересекающую её в точке $A$ (рис. 5). Докажем, что $α ⊥ β$ .

Плоскости $α$ и $β$ пересекаются по некоторой прямой $A C$ . Так как прямая $A B$ перпендикулярна к плоскости $β$ , то прямая $A B$ перпендикулярна к любой прямой в этой плоскости, значит $A B ⊥ A C$ .

Если в плоскости $β$ провести прямую $A D$ , перпендикулярную к прямой $A C$ , угол $B A D$ будет представлять собой линейный угол двугранного угла $D A C B$ (двугранный угол, образованный при пересечении плоскостей $α$ и $β$ ). При этом $∠ B A D = 90 °$ , так как прямая $A B$ перпендикулярна к плоскости $β$ . Следовательно, угол между плоскостями $α$ и $β$ равен $90 °$ . Значит $α ⊥ β$ .

Теорема доказана.

Из рассмотренного признака перпендикулярности двух плоскостей следует, что плоскость, перпендикулярная к прямой, по которой пересекаются две данные плоскости, перпендикулярна к каждой из данных плоскостей.

Пример 2

Прямая $D A$ проходит через вершину треугольника $A B C$ , причём $D A ⊥ A B$ и $D A ⊥ A C$ . Докажите перпендикулярность плоскостей $D A C$ и $A B C$ .

Решение

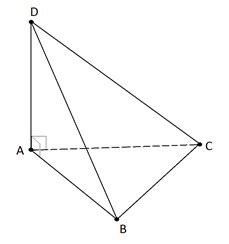Рис. 6.

Прямая $D A$ перпендикулярна к пересекающимся прямым $A B$ и $A C$ (рис. 6).

Следовательно, прямая $D A$ перпендикулярна к плоскости $A B C$ . Значит, плоскость $A D C$ проходит через прямую $A D$ , перпендикулярную плоскости $A B C$ . По признаку перпендикулярности плоскостей плоскость $D A C$ перпендикулярна плоскости $A B C$ . Что и требовалось доказать.

Пример 3

Дан параллелепипед $A B C D A_{1} B_{1} C_{1} D_{1}$ , все грани которого прямоугольники. Вычислите градусную меру двугранного угла $A D C A_{1},$ если $A C = 13$ см, $A В = 5$ см, $A A_{1} = 12 \sqrt{3}$ см.

Решение

Рис. 7

$A A_{1} ⊥ (A B C)$ , $A_{1} D$ — наклонная к $(A B C)$ ,
$A D$ — проекция наклонной $A_{1} D$ на $(A B C)$ , $A D ⊥ C D$ (по определению прямоугольника), тогда по теореме о трех перпендикулярах $A_{1} D ⊥ C D$ . Значит, $∠ A D A_{1}$ — линейный угол двугранного угла $A D C A_{1}$ .

Из треугольника $A C D$ , по теореме Пифагора, $A D = 12$ см.

Из треугольника $A A_{1} D$ : $tg A D A_{1} = \frac{A A_{1}}{A D} = \sqrt{3}$ , следовательно, $∠ A D A_{1} = 60 °$ .

Ответ: $60 °$ .

Контрольные вопросы

Что называют двугранным углом?
Что принимают за градусную меру двугранного угла?
Какие плоскости называют взаимно перпендикулярными?
Сформулируйте признак перпендикулярности двух плоскостей.

Ответы

Упражнение 1

6 см.
30^o.

Конспект урока: Двугранный угол. Признак перпендикулярности двух плоскостей

Взаимное расположение прямых и плоскостей в пространстве

Двугранный угол

Признак перпендикулярности двух плоскостей