Цифровая библиотека

Интернет-библиотека по школьным предметам от «Онлайн-школы». Библиотека поможет решить домашнее задание, подготовиться к контрольной и вспомнить прошлые темы.

Например: формулы сокращенного умножения

Выбери класс

Выбери все классы

Все предметы
10 класс
Геометрия
Перпендикулярные прямые в пространстве. Параллельные прямые, перпендикулярные к плоскости. Признак перпендикулярности прямой и плоскости. Теорема о прямой, перпендикулярной к плоскости

Геометрия 10 класс Геометрия 10 класс

Конспект урока: Перпендикулярные прямые в пространстве. Параллельные прямые, перпендикулярные к плоскости. Признак перпендикулярности прямой и плоскости. Теорема о прямой, перпендикулярной к плоскости

Взаимное расположение прямых и плоскостей в пространстве

23.04.2024

2911

Перпендикулярность прямых и плоскостей. Перпендикулярность прямой и плоскости

План урока

Перпендикулярные прямые в пространстве;
Параллельные прямые, перпендикулярные к плоскости;
Признак перпендикулярности прямой и плоскости;
Теорема о прямой, перпендикулярной к плоскости.

Цели урока

Знать определение перпендикулярных прямых;
Знать какая прямая называется перпендикулярной к плоскости;
Знать формулировки основных теорем, связанных с перпендикулярностью прямой и плоскости;
Знать и уметь доказывать признак перпендикулярности прямой и плоскости;
Уметь применять при решении задач рассмотренные определения и теоремы.

Разминка

Как определяют угол между пересекающимися прямыми?
Как определяют угол между скрещивающимися прямыми?
Каким может быть взаимное расположение прямой и плоскости?

Перпендикулярные прямые в пространстве

В курсе планиметрии уже давалось определение перпендикулярных прямых. Говорили, что две пересекающиеся прямые называются перпендикулярными, если они образуют четыре прямых угла. В данном определении можно было бы и не уточнять, что прямые пересекающиеся, так как если прямые на плоскости образуют прямой угол (или любой другой отличный от нуля угол), то это означало, что прямые пересекаются. Однако в стереометрии кроме параллельных и пересекающихся прямых существуют ещё и скрещивающиеся прямые. Перпендикулярность прямых в пространстве определяется следующим образом.

Определение 1

Две прямые в пространстве называются перпендикулярными (взаимно перпендикулярными) , если угол между ними равен $90 °$ .

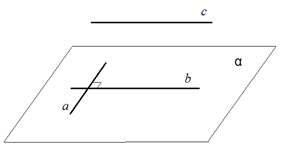Рис. 1.

Таким образом, перпендикулярные прямые могут пересекаться (прямые $a$ и $b$ на рис. 1), но могут быть и скрещивающимися (прямые $a$ и $c$ на рис. 1). Перпендикулярность прямых, изображённых на рисунке можно записать так: $a ⊥ b$ , $a ⊥ c$ .

Сформулируем и докажем лемму о перпендикулярности двух параллельных прямых к третьей прямой.

Лемма

Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой.

Доказательство

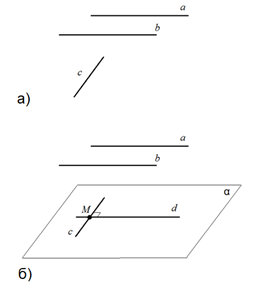Рис. 2.

Пусть прямые $a$ и $b$ параллельны, а прямые $a$ и $c$ перпендикулярны (рис. 2 а). Другими словами, угол между прямыми $a$ и $c$ равен $90 °$ .

Докажем, что прямые $b$ и $c$ тоже перпендикулярны.

Отметим на прямой $c$ некоторую точку $M$ . Через эту точку проведём прямую $d$ , параллельную прямой $a$ (рис. 2б). Угол между прямыми $d$ и $c$ равен углу между прямыми $a$ и $c$ . Значит, угол между прямыми $d$ и $c$ равен $90 ° .$ Так как $b ∥ a$ и
$a ∥ d$ , то $b ∥ d$ .

Следовательно, угол между прямыми $b$ и $c$ равен углу между прямыми $d$ и $c$ . Таким образом, угол между прямыми $b$ и $c$ тоже равен $90 °$ , то есть прямые $b$ и $c$ перпендикулярны.

Лемма доказана.

Пример 1

В тетраэдре $S A B C$ $B C ⊥ S A$ . Докажите, что $S A ⊥ M N$ , где $M$ , $N$ – середины рёбер $A B$ и $A C$ соответственно.

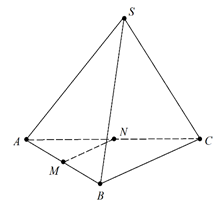Рис. 3.

Доказательство

Так как $M$ , $N$ – середины рёбер $A B$ и $A C$ (рис. 3), то $M N$ – средняя линия треугольника $A B C$ . Следовательно, $M N ∥ B C$ .

По условию $B C ⊥ S A$ . Тогда, по доказанной лемме, $M N ⊥ S A$ . Что и требовалось доказать.

Параллельные прямые, перпендикулярные к плоскости

Определение 2

Прямая называется перпендикулярной к плоскости , если она перпендикулярна к любой прямой, лежащей в этой плоскости.

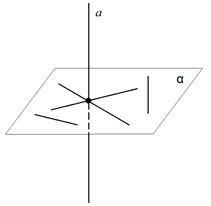Рис. 4.

Очевидно, что прямая, перпендикулярная к некоторой плоскости, пересекает её. Действительно, если прямая $a$ не пересекала бы плоскость $α$ , то она или лежала бы в этой плоскости, или была бы параллельна ей. В таком случае в плоскости $α$ имелись бы прямые не перпендикулярные к прямой $a$ . Это противоречит тому, что прямая a и плоскость $α$ перпендикулярны. На рисунке 4 показана прямая $a$ , перпендикулярная ей плоскость $α$ и несколько прямых, лежащих в этой плоскости. Прямая $a$ перпендикулярна каждой из этих прямых, как и любой прямой в плоскости $α$ .

Теорема 1

Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости.

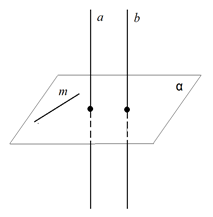Рис. 5. К теореме 1

Доказательство

Рассмотрим две параллельные прямые $a$ и $b$ и плоскость $α$ , перпендикулярную прямой $a$ (рис. 5). Докажем, что и прямая $b$ тоже перпендикулярна плоскости $α$ .

Проведём в плоскости $α$ какую-нибудь прямую $m$ .

Так как $a ⊥ α$ , то $a ⊥ m$ . По лемме о перпендикулярности двух параллельных прямых к третьей $b ⊥ m$ . Так как прямая $m$ была выбрана в плоскости $α$ произвольно, то это означает, что прямая $b$ перпендикулярна к любой прямой в плоскости $α$ . Следовательно, $b ⊥ α$ .

Теорема доказана.

Теорема 2

Если две прямые перпендикулярны к плоскости, то они параллельны.

Доказательство

Рис. 6.

Рассмотрим прямые $a$ и $b$ , перпендикулярные к плоскости $α$ (рис. 6). Докажем, что $a ∥ b$ . Через произвольную точку $M$ , лежащую на прямой $b$ , проведём прямую $b_{1}$ , параллельную прямой $a$ (рис. 6). Так как прямая $a$ перпендикулярна плоскости $α$ , то и проведённая прямая $b_{1}$ перпендикулярна плоскости $α$ (Теорема 1). Докажем, что прямая $b_{1}$ совпадает с прямой b. Предположим, что прямые $b_{1}$ и $b$ не совпадают. Обозначим плоскость, проходящую через прямые $b$ и $b_{1}$ буквой $β$ . Таким образом, в плоскости $β$ через точку $M$ проходят две прямые, перпендикулярные к прямой $c$ , по которой пересекаются плоскости $α$ и $β$ . Это невозможно. Следовательно, предположение, что $b$ и $b_{1}$ не совпадают, неверно. А так как $b$ и $b_{1}$ совпадают, то $a ∥ b$ . Теорема доказана.

Упражнение 1

1. Прямая $K S$ , перпендикулярная к плоскости правильного треугольника $M N K$ . Через центр $O$ этого треугольника проведена прямая $O P$ , параллельная $K S$ . Известно, что $M N = 8 \sqrt{3} с м$ , $O P = 6 с м,$ $K S = 8 с м$ . Найдите расстояния от точек $S$ и $P$ до вершин $M$ и $N$ треугольника.

2. Через точки $M_{1}$ и $N_{1}$ , не лежащие в плоскости $α$ , проведены прямые, перпендикулярные к плоскости $α$ и пересекающие её соответственно в точках $M_{2}$ и $N_{2}$ . Найдите $M_{2} N_{2}$ , если $M_{1} N_{1} = 30 с м$ , $M_{1} M_{2} = 43 с м$ , $N_{1} N_{2} = 67 с м$ .

Признак перпендикулярности прямой и плоскости

Теорема 3

Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.

Доказательство

Пусть некоторая прямая $a$ перпендикулярна к прямым $p$ и $q$ . Обозначим плоскость, в которой лежат эти прямые буквой $α$ . Докажем, что прямая $a$ перпендикулярна к плоскости $α$ . Для этого проведём в плоскости $α$ произвольную прямую m и докажем, что прямая $a$ перпендикулярна к этой прямой.

Рис. 7.

1) Рассмотрим сначала случай, когда прямая $a$ проходит через точку $O$ (рис. 7). Проведём через точку $O$ прямую $l$ , параллельную прямой $m$ . Отметим на прямой $a$ точки $A$ и $B$ так, чтобы точка $O$ делила отрезок $A B$ пополам. Проведём в плоскости $α$ прямую, пересекающую прямые $p$ , $q$ и $l$ соответственно в точках $P$ , $Q$ и $L$ .

Так как точка $O$ – середина отрезка $A B$ , то прямые $p$ и $q$ являются серединными перпендикулярами к отрезку $A B$ .

Следовательно, $A P = B P$ и $A Q = B Q$ . Таким образом, треугольники $A P Q$ и $B P Q$ равны по трём сторонам. Поэтому равны углы $A P Q$ и $B P Q$ .

Рассмотрим треугольники $A P L$ и $B P L$ . У них $A P = B P$ , $P L$ – общая сторона, углы $A P L$ и $B P L$ равны (было показано равенство углов $A P Q$ и $B P Q$ , которые являются соответственно углами $A P L$ и $B P L$ ). Поэтому треугольники $A P L$ и $B P L$ равны по двум сторонам и углу между ними. Из равенства треугольников $A P L$ и $B P L$ вытекает равенство отрезков $A L$ и $B L$ . Это означает, что треугольник $A B L$ равнобедренный, а его медиана $L O$ является высотой. Следовательно, $l ⊥ a$ . Так как прямые $m$ и $l$ параллельны, то по лемме о перпендикулярности двух параллельных прямых к третьей, $m ⊥ a$ . Это означает, что прямая $a$ перпендикулярна к любой прямой плоскости $α$ , т. е. прямая $a$ перпендикулярна к плоскости $α$ .

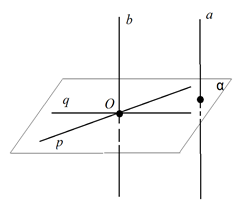Рис. 8.

2) В том случае если прямая $a$ не проходит через точку $O$ , можно провести через точку $O$ прямую $b$ , параллельную прямой $a$ (рис. 8). Прямая $b$ , согласно лемме, перпендикулярна прямым $p$ и $q$ , а по доказанному в первом случае, прямая $b$ перпендикулярна к плоскости $α$ . Отсюда следует, что и прямая $a$ перпендикулярна к плоскости $α$ .

Теорема доказана.

Через любую точку пространства проходит единственная плоскость, перпендикулярная к данной прямой.

Упражнение 2

Через вершину $B$ прямоугольника $A B C D$ проведена прямая $B M$ . Известно, что $∠ M B A = ∠ M B C = 90 °$ ; $M B = 3 с м$ ; $A B = 4 с м$ ; $B C = 12 с м$ . Найдите расстояние $M D$ .

Теорема о прямой, перпендикулярной к плоскости

Теорема 4

Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.

Доказательство

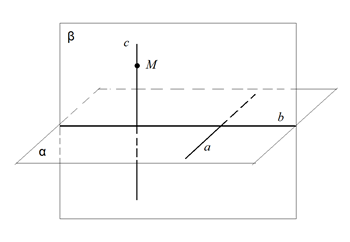Рис. 9.

Рассмотрим произвольную плоскость $α$ и точку M. Докажем, что:

1) через точку M проходит прямая, перпендикулярная к плоскости $α$ ;

2) такая прямая единственная.

1) Проведём в плоскости $α$ произвольную прямую $a$ и рассмотрим плоскость $β$ , проходящую через точку $M$ и перпендикулярную к прямой $a$ (Рис. 9). Плоскости $α$ и $β$ пересекаются по некоторой прямой $b$ . В плоскости $β$ через точку $M$ проведём прямую $c$ , перпендикулярную к прямой $b$ .

$c ⊥ b$ по построению;

$c ⊥ a$ , так как $β ⊥ a$ .

Так как прямая c перпендикулярна к двум пересекающимся прямым в плоскости $α$ , то прямая c перпендикулярна к плоскости $α$ .

2) Если через точку $M$ проходит ещё одна некоторая прямая $d$ , перпендикулярная к плоскости $α$ , то $c ∥ d$ (Теорема 2), а это невозможно, так как прямые $c$ и $d$ пересекаются в точке $M$ . Значит, $c$ – единственная прямая, проходящая через точку $M$ и перпендикулярная к плоскости $α$ .

Теорема доказана.

Контрольные вопросы

1. Могут ли перпендикулярные прямые не пересекаться?

2. Какая прямая называется перпендикулярной к данной плоскости?

3. Сформулируйте признак перпендикулярности прямой и плоскости.

4. Сформулируйте теорему о прямой, перпендикулярной к плоскости.

Ответы

Упражнение 1

1. SM=SN=16 см; PM=PN=10 см.

2. 18 см.

Упражнение 2

13 см.

Предыдущий урок

Скрещивающиеся прямые. Углы с сонаправленными сторонами. Угол между прямыми

Взаимное расположение прямых и плоскостей в пространстве

Следующий урок

Симметрия в пространстве. Понятие правильного многогранника. Элементы симметрии правильных многогранников

Общие сведения из стереометрии

Формулы приведения

Алгебра
Человечество — мозаика рас и народов

География
Равномерное движение по окружности

Физика

Зарегистрируйся, чтобы присоединиться к обсуждению урока

Добавьте свой отзыв об уроке, войдя на платфому или зарегистрировавшись.

Отзывы об уроке:

Пока никто не оставил отзыв об этом уроке