Все уроки по всем предметам школьной программы ФГОС

Прямоугольный параллелепипед

План урока

Прямоугольный параллелепипед

Цели урока

Знать свойства прямоугольного параллелепипеда
Уметь вычислять диагональ прямоугольного параллелепипеда по его измерениям

Разминка

Что такое параллелепипед?
Какие плоскости называются перпендикулярными?
Как вычислить диагональ прямоугольника по его измерениям?

Прямоугольный параллелепипед

Рис. 1.

В жизни мы часто сталкиваемся с предметами, имеющими форму прямоугольного параллелепипеда. Наглядными примерами таких предметов являются кирпич, коробка, холодильник, системный блок компьютера и т. д.

Параллелепипед называется прямоугольным, если его боковые рёбра перпендикулярны к основанию, а основания представляют собой прямоугольники.

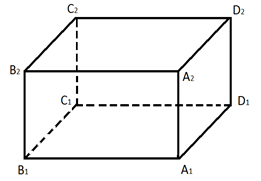Рис. 2. Прямоугольный параллелепипед

Основаниями прямоугольного параллелепипеда $A_{1} B_{1} C_{1} D_{1} A_{2} B_{2} C_{2} D_{2}$ на рисунке 2 служат прямоугольники $A_{1} B_{1} C_{1} D_{1}$ и $A_{2} B_{2} C_{2} D_{2}$ . Согласно определению, боковые рёбра $A_{1} A_{2}$ , $B_{1} B_{2}$ , $C_{1} C_{2}$ , $D_{1} D_{2}$ перпендикулярны к основаниям. Из этого следует, что боковые грани являются прямоугольниками. Таким образом, прямоугольный параллелепипед обладает следующими свойствами:

Свойства прямоугольного параллелепипеда

В прямоугольном параллелепипеде все шесть граней – прямоугольники.
Все двугранные углы прямоугольного параллелепипеда – прямые.

Длины непараллельных рёбер прямоугольного параллелепипеда называются его линейными размерами (измерениями). У прямоугольного параллелепипеда три измерения. Часто эти измерения называют «длина», «ширина» и «высота». Например, на рисунке 2 в качестве измерений можно взять ребра $A_{1} A_{2}$ , $A_{1} B_{1}$ , $A_{1} D_{1}$ .

Прямоугольный параллелепипед, у которого все три измерения равны, называется кубом.

Все грани куба – равные квадраты.

Сформулируем и докажем свойство диагонали прямоугольного параллелепипеда.

Свойство диагонали прямоугольного параллелепипеда

Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.

Доказательство

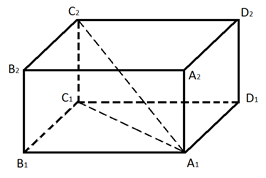Рис. 3. К доказательству теоремы 1

Рассмотрим прямоугольный параллелепипед $A_{1} B_{1} C_{1} D_{1} A_{2} B_{2} C_{2} D_{2}$ (рис. 3) и докажем, что

$A_{1} {C_{2}}^{2} = A_{1} {B_{1}}^{2} + A_{1} {D_{1}}^{2} +$

$+ A_{1} {A_{2}}^{2}$

Так как ребро $C_{1} C_{2}$ перпендикулярно к основанию $A_{1} B_{1} C_{1} D_{1}$ , то угол $A_{1} C_{1} C_{2}$ прямой.

Из прямоугольного треугольника $A_{1} C_{1} C_{2}$ по теореме Пифагора получаем

$A_{1} {C_{2}}^{2} = A_{1} {C_{1}}^{2} + C_{1} {C_{2}}^{2}$ .

$A_{1} C_{1}$ – диагональ прямоугольника $A_{1} B_{1} C_{1} D_{1}$ . Значит,

$A_{1} {C_{1}}^{2} = A_{1} {B_{1}}^{2} + A_{1} {D_{1}}^{2}$ .

При этом $C_{1} C_{2} = A_{1} A_{2}$ . Следовательно,

$A_{1} {C_{2}}^{2} = A_{1} {B_{1}}^{2} + A_{1} {D_{1}}^{2} + A_{1} {A_{2}}^{2}$ .

Теорема доказана.

Из теоремы следует, что диагонали прямоугольного параллелепипеда равны.

Пример 1

Найдите измерения прямоугольного параллелепипеда, если его измерения относятся как 2:3:6, а диагональ параллелепипеда равна 28 см.

Решение

Измерения прямоугольного параллелепипеда $A_{1} B_{1} C_{1} D_{1} A_{2} B_{2} C_{2} D_{2}$ (рис. 3) относятся как 2:3:6, тогда можно принять, что

$A_{1} B_{1} = 2 x$ , $A_{1} D_{1} = 3 x$ , $A_{1} A_{2} = 6 x$ .

Так как $A_{1} {C_{2}}^{2} = A_{1} {B_{1}}^{2} + A_{1} {D_{1}}^{2} + A_{1} {A_{2}}^{2}$ , то получим уравнение

$4 x^{2} + 9 x^{2} + 36 x^{2} = 28^{2}$ ,

$49 x^{2} = 28^{2}$ ,

$x^{2} = \frac{28^{2}}{49}$ ,

$x^{2} = 16$ ,

$x = 4$ .

$A_{1} B_{1} = 8 с м$ , $A_{1} D_{1} = 12 с м$ , $A_{1} A_{2} = 24 с м$ .

Ответ: 8 см, 12 см, 24 см.

Пример 2

Диагональ прямоугольного параллелепипеда равна 10 см, а диагональ одной из его граней – 8 см. Найдите длину ребра, перпендикулярного к данной грани.

Решение

По условию задачи $A_{1} C_{2} = 10 с м$ .

Пусть диагональ грани $A_{1} B_{1} C_{1} D_{1}$ прямоугольного параллелепипеда $A_{1} B_{1} C_{1} D_{1} A_{2} B_{2} C_{2} D_{2}$ равна 8 см. Значит, $A_{1} C_{1} = 8 с м$ . В таком случае требуется найти ребро $С_{1} С_{2}$ (рис. 3). Треугольник $C_{1} C_{2} A_{1}$ – прямоугольный с прямым углом $C_{1}$ . По теореме Пифагора:

$C_{1} {C_{2}}^{2} = A_{1} {C_{2}}^{2} - A_{1} {C_{1}}^{2} = 10^{2} - 8^{2} = 100 - 64 = 36$ ,

$C_{1} C_{2} = 6 с м$ .

Ответ: $6$ см.

Пример 3

Найдите измерения прямоугольного параллелепипеда $A_{1} B_{1} C_{1} D_{1} A_{2} B_{2} C_{2} D_{2}$ , если $A_{1} C_{2} = 24 с м$ и диагональ $B_{1} D_{2}$ составляет с плоскостью грани $A_{1} A_{2} D_{2} D_{1}$ угол в 30^o, а с ребром $D_{1} D_{2}$ – угол в 45^o.

Решение

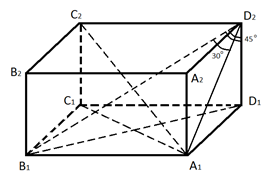Рис. 4.

Так как диагонали прямоугольного параллелепипеда равны, то $B_{1} D_{2} = A_{1} C_{2} = 24 с м$ .

В прямоугольном треугольнике $B_{1} D_{1} D_{2}$ $∠ D_{1} D_{2} B_{1} = 45 ° \Rightarrow ∠ D_{1} B_{1} D_{2} = 45 °$ .

Следовательно, прямоугольный треугольник $D_{1} D_{2} B_{1}$ является равнобедренным, в котором $B_{1} D_{1} = D_{1} D_{2}$ и $B_{1} D_{2} = 24 с м$ .

Обозначим $B_{1} D_{1} = D_{1} D_{2}$ за $x$ .

По теореме Пифагора:

$x^{2} + x^{2} = 24^{2}$ ,

$2 x^{2} = 576$ ,

$x^{2} = 288$ ,

$x = 12 \sqrt{2}$ .

Таким образом, $B_{1} D_{1} = D_{1} D_{2} = 12 \sqrt{2}$ см.

Отрезок $A_{1} D_{2}$ является проекцией диагонали $B_{1} D_{2}$ на плоскость грани $A_{1} A_{2} D_{2} D_{1}$ .

Значит, углом между диагональю $B_{1} D_{2}$ и гранью $A_{1} A_{2} D_{2} D_{1}$ является угол $A_{1} D_{2} B_{1}$ , т.е. $∠ A_{1} D_{2} B_{1} = 30 °$ .

Треугольник $A_{1} D_{2} B_{1}$ – прямоугольный с прямым углом $A_{1}$ . Гипотенуза $B_{1} D_{2}$ этого треугольника равна 24 см.

Следовательно, катет $A_{1} B_{1}$ , лежащий против угла $A_{1} D_{2} B_{1}$ , равного 30^o, равен 12 см.

В прямоугольном треугольнике $A_{1} B_{1} D_{1}$ известна гипотенуза $B_{1} D_{1} = 12 \sqrt{2} с м$ и катет $A_{1} B_{1} = 12 с м$ .

Тогда $A_{1} D_{1} = \sqrt{B_{1} {D_{1}}^{2} - A_{1} {B_{1}}^{2}} = \sqrt{288 - 144} = \sqrt{144} = 12 с м$ .

Таким образом $A_{1} B_{1} = A_{1} D_{1} = 12 с м$ , $D_{1} D_{2} = 12 \sqrt{2} с м$ .

Ответ: $12 с м$ , $12 с м$ , $12 \sqrt{2} с м$ .

Упражнение 1

1. Найдите диагональ прямоугольного параллелепипеда, если его измерения равны 16 см, 18 см и 24 см.

2. Ребро куба равно 2 м. Найдите его диагональ.

3. Найдите косинус угла между диагональю куба и плоскостью одной из его граней.

Контрольные вопросы

Какой параллелепипед называется прямоугольным?
Сформулируйте основные свойства прямоугольного параллелепипеда.
Сформулируйте теорему о диагонали прямоугольного параллелепипеда.
Сформулируйте признак перпендикулярности двух плоскостей.
Какую фигуру называют кубом?

Ответы

Упражнение 1

$34$ см.
$2 \sqrt{3}$ м.
$\sqrt{\frac{2}{3}}$ .

Конспект урока: Прямоугольный параллелепипед

Призма

Прямоугольный параллелепипед